3.2,2. Прямая и точка, лежащие в плоскости
|
Пусть задана плоскость двумя пересекающимися прямыми а и Ъ. Как построить прямую, лежащую в данной плоскости? Это построение основано на одном из двух следующих положений. Прямая принадлежит плоскости (инцидентна ей):
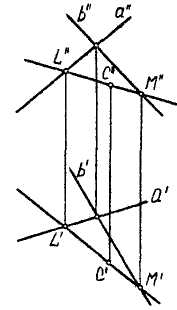
Построим прямую, лежащую в плоскости а ( anb ), через две точки, заведомо принадлежащие плоскости: точку lea и точку Мей (рис. 3.8). Точка принадлежит плоскости, если она лежит на прямой, принадлежащей этой плоскости. Точка С лежит на прямой LM, принадлежащей плоскости a (anb).
|
Рис. 3.8 |
3.2.3. Главные линии плоскости
К главным линиям плоскости относятся линии уровня плоскости. Прямые линии, лежащие в плоскости и параллельные плоскостям проекций, называют линиями уровня данной плоскости.
|
|
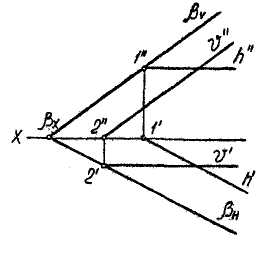
1) Горизонталь - прямая, принадлежащая плоскости и параллельная горизонтальной плоскости проекции, h || H. Построение горизонтали (рис. 3.9, а) начинают с ее фронтальной проекции Отметим, что горизонтали одной и той же плоскости параллельны между собой. 2) Фропталь - прямая, принадлежащая плоскости и параллельная фронтальной плоскости. Построение фронтали начинаем с ее горизонтальной проекции. Все фронтали одной плоскости параллельны между собой. |
3.2.4. Плоскости общего и частных положений
Если плоскость наклонена ко всем плоскостям проекций, такую плоскость называют плоскостью общего положения.
Примерами плоскостей общего положения могут служить все плоскости, рассмотренные в разделе 3.2.1.
Частные случаи расположения плоскостей
А. Проецирующие плоскости
Плоскость, перпендикулярная к одной из плоскостей проекций, называется проецирующей.
|
|
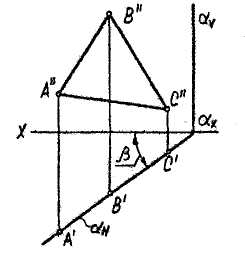
1)Горизонтально проецирующая плоскость - плоскость, перпендикулярная к Н. Рассмотрим, как изображаются проецирующие плоскости на комплексном чертеже, а также некоторые свойства проецирующих плоскостей.
|
Можно сформулировать следующее «собирательное свойство» таких плоскостей: горизонтальная проекция любой линии (точки, фигуры), лежащей в горизонтально проецирующей плоскости, совпадает с горизонтальной проекцией этой плоскости (ее горизонтальным следом). При этом β - угол наклона плоскости ос к V. Плоскость а вполне определяется одной своей проекцией.
|
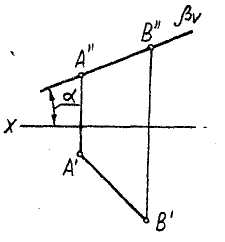
2)Фронтально проецирующая плоскость - плоскость, перпендикулярная П2 Легко представить, что для фронтально-проецирующей плоскости фронтальная проекция вырождается в прямую линию -- pv, а горизонтальная является полем точек. При этом а - угол наклона плоскости Р к плоскости П1.
|
|
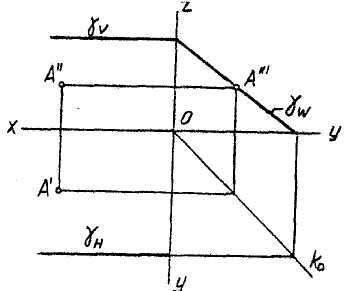
3) Профильно проецирующая плоскость - плоскость, перпендикулярная к W(П3). Очевидно, что профильно проецирующая плоскость и любые геометрические образы, расположенные в ней, н& плоскость W спроецируются в прямую линию, ее профильный след yw.
|
Б. Плоскости уровня
Среди проецирующих плоскостей важную роль играют плоскости уровня. Плоскость, параллельная какой-либо плоскости проекций, называется плоскостью уровня (рис. 3.13):