- •Линии и их проекционные свойства
- •Следы прямой
- •Взаимное расположение двух прямых
- •2.2. Кривые линии и их проекционные свойства
- •2.2.1. Плоские кривые
- •2. Касательная к кривой проецируется в касательную к ее проекции.
- •3. Число точек пересечения плоских кривых сохраняется при проецировании.
- •2.2.3. Пространственные кривые линии
- •3. Поверхности
- •3.1. Способы образования и задания поверхностей на чертеже
- •3.1.2. Задания поверхности на чертеже
- •3.2. Плоскость
- •3.2.1. Способы задания плоскости на чертеже
- •3.2,2. Прямая и точка, лежащие в плоскости
- •3.2.3. Главные линии плоскости
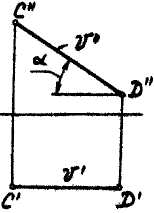
- •3.2.4. Плоскости общего и частных положений
- •Фронтальная плоскость уровня - плоскость, параллельная V;
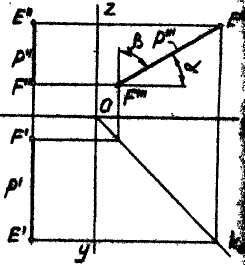
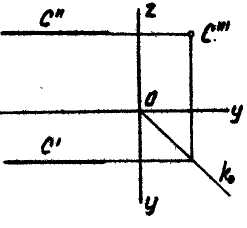
- •3)Профильная плоскость уровня - плоскость, параллельная w.
- •3.2.5. Проекции углов, проекция прямого угла
- •3.2.6. Линии наибольшего наклона
- •3.3. Линейчатые поверхности
- •Поверхности Способы образования поверхностей на чертеже
- •Плоскость
Линии и их проекционные свойства
Прямая общего положения
|
|
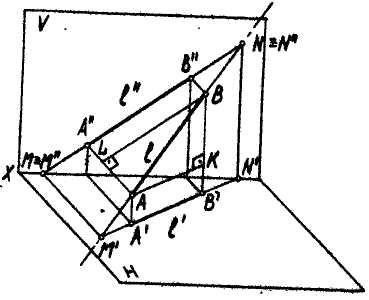
Натуральная величина отрезка равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка на любую плоскость проекций, скажем П1, а другой катет равен разности расстояний концов отрезка до той же плоскости проекций (разности высот).
|
|
||
Прямые частного положения перпендикулярны или параллельны плоскостям проекций.
Линии уровня
|
1.Горизонталь
|
2. Фронталь
|
3. Профильная прямая
|
|
Проецирующие прямые
|
1. Горизонтально – проецирующая прямая
|
2. Фронтально-проецирующая прямая
|
3.Профильно-проеци-рующая прямая
|
|
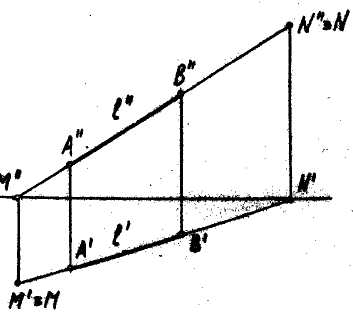
Следы прямой
|
Следами прямой линии называют точки ее пересечения с плоскостями проекций
|
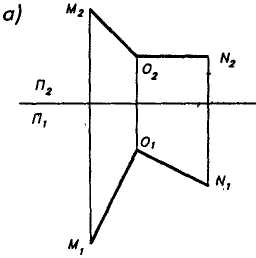
Взаимное расположение двух прямых
А. Пересекающиеся прямые:
|
Б) паралельные прямые
|
|
С)Скрещивающие
прямые.
|
Проецирование углов
|
Прямой угол, одна из сторон которого параллельна плоскости проекций, проецируется на эту плоскость в натуральную величину. |
|
2.2. Кривые линии и их проекционные свойства
Кривая называется плоской, если все ее точки принадлежат некоторой плоскости. Кривая, не лежащая всеми точками в одной плоскости, называется пространственной.
|
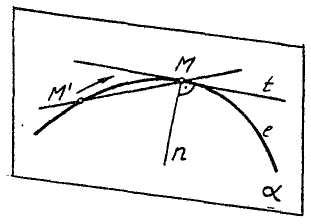
Касательной прямой t в точке М плоской кривой I называется предельное положение секущей ММ', когда М' оставаясь на кривой I, стремится к точке М Нормалью п к кривой в точке М называется прямая, лежащая в плоскости а кривой 1 и перпендикулярная к касательной t в этой точке.
|
2.2.1. Плоские кривые
А. Классификация плоских кривых
Плоские кривые подразделяются на:
1. Кривые, определяемые уравнениями алгебраическими или трансцендентными
Графические, для которых могут быть найдены уравнения лишь приближенно.
Обводы (при задании линии дискретными точками).
Б. Задание кривой на чертеже
В общем случае для полного графического задания кривой необходимо задать две ее проекции на комплексном чертеже.
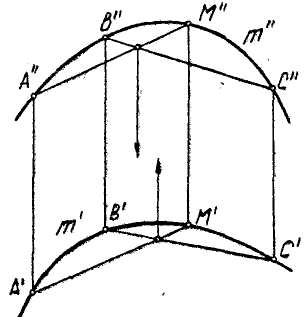
В. Порядок кривой

Г. Основные свойства проекций плоских кривых линий
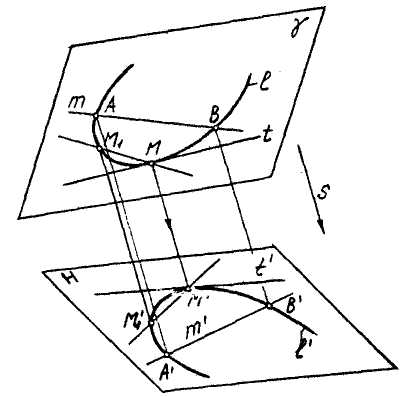
/. Порядок плоской алгебраической кривой при параллельном проецировании не изменяется.
2. Касательная к кривой проецируется в касательную к ее проекции.
3. Число точек пересечения плоских кривых сохраняется при проецировании.
Д. Классификация точек кривой
К особым точкам относятся следующие:

2.2.3. Пространственные кривые линии
Порядок пространственной алгебраической кривой геометрически определяется как число точек пересечения ее с произвольной плоскостью.
Для проекций пространственных кривых линий характерны следующие свойства:
1. Пространственная кривая линия при любом ее положении в пространстве проецируется в кривую.
2. Касательная t к пространственной кривой I проецируется в касательную t' к ее проекции I', если она не проецируется в точку. Обратная же теорема не верна.
Чтобы установить характер кривой необходимо сопоставить обе проекции кривой.
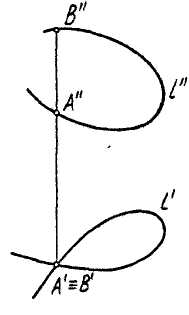
А. Цилиндрическая винтовая линия

Б. Коническая винтовая линия
В. Определение длины пространственной кривой