2 Определение комплексной оценки качества холоднокатаной ленты

Пределы изменения параметров холоднокатаной ленты представлены в таблице 2.1.

Таблица 2.1 - Предельные отклонения показателей качества

Параметр (показатель качества) холоднокатаного листа	Предельные отклонения
1 содержание углерода, %	±0,01
2 содержание кремния, %, не более	0,03
3 содержание марганца, %	±0,03
4 содержание хрома, %, не более	0,10
5 толщина, мм	-0,12
6 ширина, мм	-0,6
7 предел прочности, Н/мм²	440-590
8 относительное удлинение, %, не менее	10

Для проведения оценки качества холоднокатаной ленты был проведен анализ фактических значений отдельных единичных показателей, оказывающих наибольшее влияние на его качество.

Показатели качества:

1. Толщина

2. Ширина

3. Содержание углерода

4. Содержание кремния

5. Содержание марганца

6. Содержание хрома

7. Предел прочности

8.Относительное удлинение

1 Определим доверительный интервал фактических значений по содержанию в стали углерода..

Поизводим 25 замеров фактических значений (хi) Результаты приведены в таблице 2.1. Таблица 2.1

хi	n	xi n	n( -xi)²
0,06 0,07 0,08 0,09 0,10	10 3 0 6 6	0,60 0,21 0,00 0,54 0,60	0,0032 0,0002 0,0000 0,0009 0,0029
N=25		∑=0,0072

Строим гистограмму по замеренным значениям, на которую наносим пределы изменения С по ГОСТ 1045-81 для холоднокатаной ленты (рисунок 2.1).

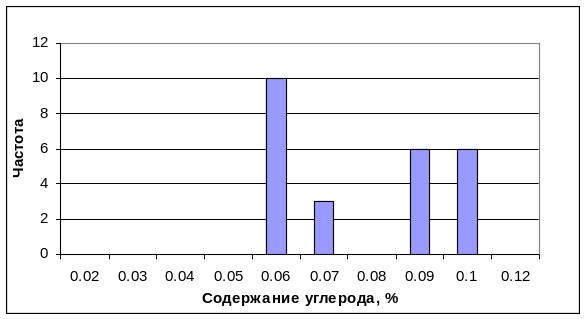
Рисунок 2.1 - Гистограмма фактических значений замеров содержания углерода

Определяем среднее арифметическое значение замеренных параметров (математическое ожидание) х и среднеквадратическое отклонение :

 ,

где х_i - намеренные значения параметра (случайная величина);

n - объем выборки.

= 0,078;

 = 0,017

Доверительный интервал фактических значений с надежностью Р=0,99 определяем с помощью правила трех сигм: отклонение истинного значения измеряемой величины от среднего арифметического значения результатов измерений не превосходит утроенной средней квадратической ошибки этого среднего значения:

х_факт = х ± 3 = 0,078 ± 0,017*3 = (0,026…0,129).

∆d=0,103;

2 Определим доверительный интервал по содержанию кремния.

Таблица 2.2 - Фактические замеры значений содержания кремния

хi	n	xin	( –xi)²
0,010 0,015 0,020 0,025 0,030	5 8 2 7 3	0,05 0,12 0,04 0,175 0,09	0,000405 0,000128 0,000002 0,000252 0,000363
N=25		∑=0,00115

Строим гистограмму по замеренным значениям, на которую наносим пределы изменения Si по ГОСТ 1045-81 для холоднокатаной ленты (рисунок 2.2).

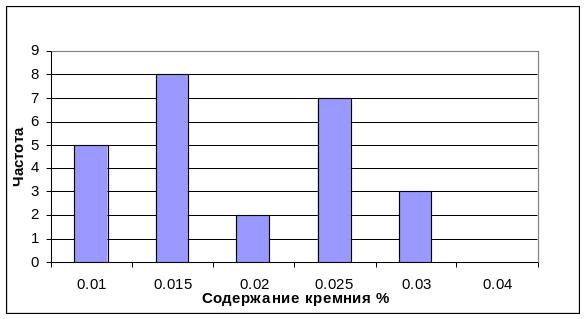
Рисунок 2.2 - Гистограмма фактических значений замеров содержания кремния

Определяем среднее арифметическое значение замеренных параметров (математическое ожидание) х и среднеквадратическое отклонение :

 ,

где х_i - намеренные значения параметра (случайная величина);

n - объем выборки.

= 0,019,%;

 = 0,0069, %.

Доверительный интервал фактических значений с надежностью Р=0,99 определяем с помощью правила трех сигм: отклонение истинного значения измеряемой величины от среднего арифметического значения результатов измерений не превосходит утроенной средней квадратической ошибки этого среднего значения:

х_факт = х ± 3 = 0,019 ± 0,0069*3 = (0,0…0,04) %.

То есть доверительный интервал для содержания кремния

∆d=0,04;

3 Определим доверительный интервал по содержанию марганца.

Таблица 2.3 - Фактические замеры значений содержания марганца

xi	n	xin	( -xi)²
0,30 0,40	8 17	2,40 6,80	0,037 0,017
N=25		∑=0,054

Строим гистограмму по замеренным значениям, на которую наносим пределы изменения Mn по ГОСТ 1045-81 для холоднокатаной ленты (рисунок 2.3).

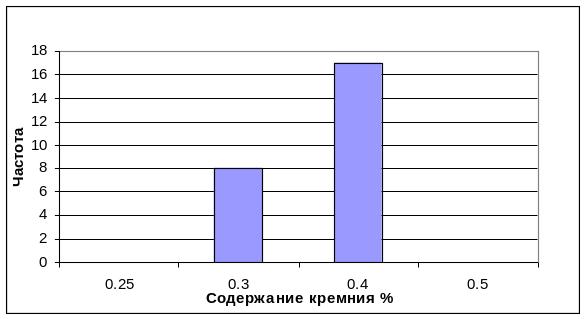
Рисунок 2.3 - Гистограмма фактических значений замеров содержания марганца

Определяем среднее арифметическое значение замеренных параметров (математическое ожидание) х и среднеквадратическое отклонение :

 ,

где х_i - намеренные значения параметра (случайная величина);

n - объем выборки.

= 0,368,%;

 = 0,048, %.

Доверительный интервал фактических значений с надежностью Р=0,99 определяем с помощью правила трех сигм: отклонение истинного значения измеряемой величины от среднего арифметического значения результатов измерений не превосходит утроенной средней квадратической ошибки этого среднего значения:

х_факт = х ± 3 = 0,368 ± 0,048*3 = (0,225…0,511) %.

То есть доверительный интервал для содержания марганца

∆d=0,286;

4. Определим доверительный интервал по содержанию хрома.

Таблица 2.4 - Фактические замеры значений содержания хрома

хi	n	xin	( -xi)²
0,001 0,002 0,003 0,004 0,005	2 5 8 4 6	0,002 0,010 0,028 0,016 0,030	0,0000104 0,0000082 0,0000006 0,0000021 0,0000178
N=25		∑=0,000039

Строим гистограмму по замеренным значениям, на которую наносим пределы изменения Cr по ГОСТ 1045-81 для холоднокатаной ленты (рисунок 2.4).

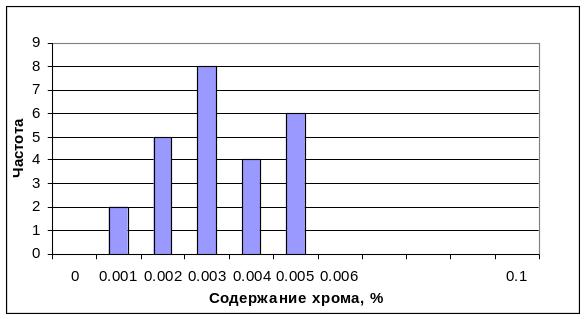
Рисунок 2.4 - Гистограмма фактических значений замеров содержания хрома

Определяем среднее арифметическое значение замеренных параметров (математическое ожидание) х и среднеквадратическое отклонение :

 ,

где х_i - намеренные значения параметра (случайная величина);

n - объем выборки.

= 0,0033,%;

 = 0,0013, %.

Доверительный интервал фактических значений с надежностью Р=0,99 определяем с помощью правила трех сигм: отклонение истинного значения измеряемой величины от среднего арифметического значения результатов измерений не превосходит утроенной средней квадратической ошибки этого среднего значения:

х_факт = х ± 3 = 0,0033 ± 0,0013*3 = (0,000…0,0071) %.

То есть доверительный интервал для содержания хрома

∆d=0,0071;

5 Определим доверительный интервал для толщины.

Таблица 2.5 - Фактические замеры значений толщины

хi	n	xin	( -xi)²
2,40 2,50	11 14	26,4 35,0	0,035 0,027
N=25		∑=0,062

Строим гистограмму по замеренным значениям, на которую наносим пределы изменения толщины по ГОСТ 503-88 для холоднокатаной ленты (рисунок 2.5).

Рисунок 2.5 - Гистограмма фактических значений толщины

Определяем среднее арифметическое значение замеренных параметров (математическое ожидание) х и среднеквадратическое отклонение :

 ,

где х_i - намеренные значения параметра (случайная величина);

n - объем выборки.

= 2,456 мм;

 = 0,05 мм.

Доверительный интервал фактических значений с надежностью Р=0,99 определяем с помощью правила трех сигм: отклонение истинного значения измеряемой величины от среднего арифметического значения результатов измерений не превосходит утроенной средней квадратической ошибки этого среднего значения:

х_факт = х ± 3 = 2,456 ± 0,05*3 = (2,3…2,6) мм.

То есть доверительный интервал для толщины

∆d=0,3 мм;

6. Определим доверительный интервал для ширины.

Таблица 2.6 - Фактические замеры значений ширины

хi	n	xin	( -xi)²
148,5 148,6 148,7 148,8 148,9 149,0	5 2 0 14 2 2	742,5 297,2 0,0 2083,2 297,8 298	0,308 0,044 0 0,038 0,046 0,127
N=25		∑=0,562

Строим гистограмму по замеренным значениям, на которую наносим пределы изменения ширины по ГОСТ 503-88 для холоднокатаной ленты (рисунок 2.6).

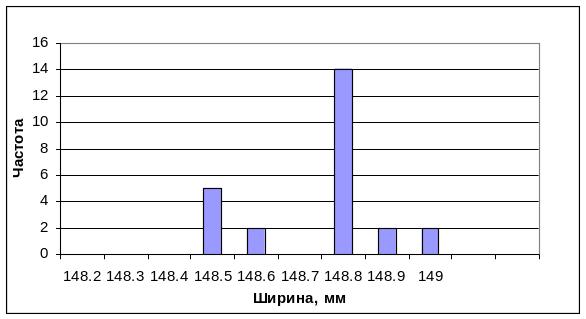
Рисунок 2.6 - Гистограмма фактических значений ширины

Определяем среднее арифметическое значение замеренных параметров (математическое ожидание) х и среднеквадратическое отклонение :

 ,

где х_i - намеренные значения параметра (случайная величина);

n - объем выборки.

= 148,75 мм;

 = 0,153 мм.

Доверительный интервал фактических значений с надежностью Р=0,99 определяем с помощью правила трех сигм: отклонение истинного значения измеряемой величины от среднего арифметического значения результатов измерений не превосходит утроенной средней квадратической ошибки этого среднего значения:

х_факт = х ± 3 = 148,75 ± 0,153*3 = (148,29…149,2) мм.

То есть доверительный интервал для ширины

∆d=0,918, мм;

7. Определим доверительный интервал для предела прочности.

Таблица 2.7 - Фактические замеры значений предела прочности

хi	n	xin	( -xi)²
465 480 495 510	14 8 0 3	6510 3840 0 1530	1456,56 184,32 0 3633,12
N=25		∑=5274

Строим гистограмму по замеренным значениям, на которую наносим пределы изменения предела прочности по ГОСТ 1045-81 для холоднокатаной ленты (рисунок 2.7).

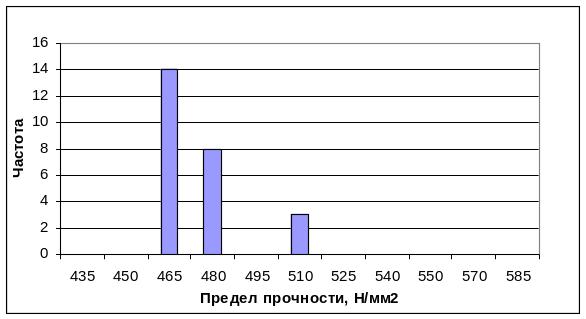
Рисунок 2.7 - Гистограмма фактических значений предела прочности

Определяем среднее арифметическое значение замеренных параметров (математическое ожидание) х и среднеквадратическое отклонение :

 ,

где х_i - намеренные значения параметра (случайная величина);

n - объем выборки.

= 475,2 Н/мм²;

 = 14,82 Н/мм².

Доверительный интервал фактических значений с надежностью Р=0,99 определяем с помощью правила трех сигм: отклонение истинного значения измеряемой величины от среднего арифметического значения результатов измерений не превосходит утроенной средней квадратической ошибки этого среднего значения:

х_факт = х ± 3 = 475,2 ± 14,82*3 = (430,73…519,67) Н/мм².

То есть доверительный интервал для предела прочности

∆d=88,94 Н/мм²;

8 Определим доверительный интервал для относительного удлинения.

Таблица 2.8 - Фактические замеры значений относительного удлинения

хi	n	xin	( -xi)²
11,5 12,0 12,5 13,0 13,5	3 10 5 4 3	34,5 120,0 62,5 52,0 40,5	2,32 1,44 0,072 1,54 3,76
N=25		∑=9,14

Строим гистограмму по замеренным значениям, на которую наносим пределы изменения относительного удлинения по ГОСТ 1045-81 для холоднокатаной ленты (рисунок 2.8).

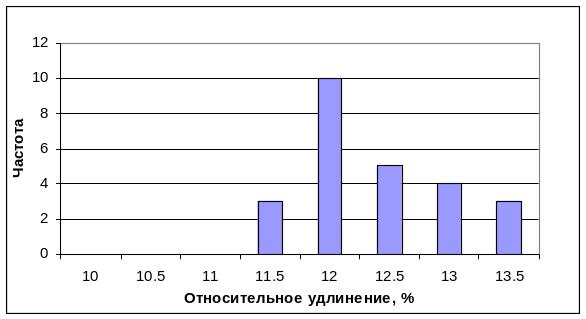
Рисунок 2.8 - Гистограмма фактических значений относительного удлинения

Определяем среднее арифметическое значение замеренных параметров (математическое ожидание) х и среднеквадратическое отклонение :

 ,

где х_i - намеренные значения параметра (случайная величина);

n - объем выборки.

= 12,38 %;

 = 0,396 %.

Доверительный интервал фактических значений с надежностью Р=0,99 определяем с помощью правила трех сигм: отклонение истинного значения измеряемой величины от среднего арифметического значения результатов измерений не превосходит утроенной средней квадратической ошибки этого среднего значения:

х_факт = х ± 3 = 12,38 ± 0,396*3 = (11,19…13,57) мм.

То есть доверительный интервал для относительного удлинения

∆d=2,38 %.