Колебательное движение. Гармоническое колебание и его характеристики. Скорость и ускорение при гармонических колебаниях.

Колебательное движение- это движения повторяющиеся через определённый промежуток времени.

Гармоническое колебание — колебания, при которых физическая величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид

или

,

где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд   — полная фаза колебаний,   — начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

Следовательно, для скорости при гармоническом колебании имеем:  ,

Следовательно, для ускорения имеем:  ,

Сложение гармонических колебаний одного направления и одинаковой частоты. Биения.

Пусть совершаются два гармонических колебания одного направления и одинаковой частоты

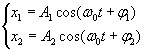 (4.1)

Уравнение результирующего колебания будет иметь вид

Убедимся в этом, сложив уравнения системы (4.1)

Применив теорему косинусов суммы и сделав алгебраические преобразования:

 (4.2)

Можно найти такие величины А и φ0 , чтобы удовлетворялись уравнения

(4.3)

Рассматривая (4.3) как два уравнения с двумя неизвестными А и φ0, найдем, возведя их в квадрат и сложив, а затем разделив второе на первое:

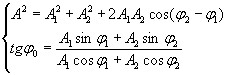
Подставляя (4.3) в (4.2), получим:

Или окончательно, используя теорему косинусов суммы, имеем:

Тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (φ2-φ1) сгладываемых колебаний.

В зависимости от разности фаз (φ2-φ1):

1) (φ2-φ1) = ±2mπ (m=0, 1, 2, …), тогда A= А1+А2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний;

2) (φ2-φ1) = ±(2m+1)π (m=0, 1, 2, …), тогда A= |А1-А2|, т. е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний

 

 

 

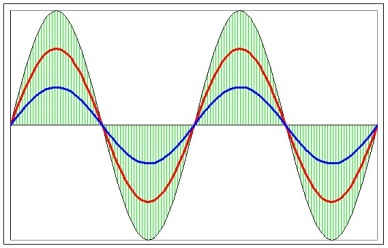
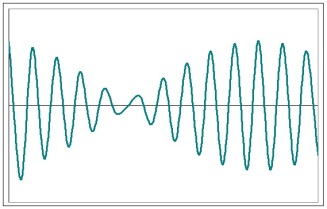
Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биением.

Пусть два колебания мало отличаются по частоте. Тогда амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω намного меньше ω. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:

Решим систему

Решение системы:

Результирующее колебание можно рассматривать как гармоническое с частотой ω, амплитуда А, которого изменяется по следующему периодическому закону:

Частота изменения А в два раза больше частоты изменения косинуса. Частота биений равна разности частот складываемых колебаний: ωб = Δω

Период биений:

 

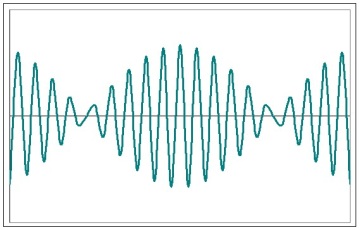
Определение частоты тона (звука определенной высоты биений эталонным и измеряемым колебаниями — наиболее широко применяемый на метод сравнения измеряемой величины с эталонной. Метод биений используется для настройки музыкальных инструментов, анализа слуха и т. д.

Сложение взаимно перпендикулярных колебаний.

Сложение взаимно перпендикулярных колебаний

Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты ω0, происходящих во взаимно перпендикулярных направлениях вдоль оси t Для простоты начальная фаза первого колебания φ0=0

где α — разность фаз обоих колебаний,

А и В — амплитуды складываемых колебаний

После несложных преобразований получим уравнение эллипса

Так как траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптическими поляризованными.

Ориентация эллипса и размеры его осей зависят от амплитуд складываемых колебаний и разности фаз α.

Некоторые частные случаи, представляющие физический интерес

1) α=mπ (m=0, ±1, ±2, …). В данном случае эллипс вырождается в отрезок прямой

где знак плюс соответствует нулю и четным значениям m (рис. а), а знак минус — нечетным значениям m (рис. б)

2) α=(2m+1)π/2 (m=0, ±1, ±2, …). В данном случае уравнение примет вид

Это уравнение эллипса, оси которого совпадают с осями координат, а его полуоси равны соответствующим амплитудам. Если А=В, то эллипс вырождается в окружность.

Динамика гармонических колебаний. Дифференциальное уравнение гармонических колебаний. Пружинный математический и физический маятник.

Обобщенное гармоническое колебание в дифференциальном виде

Итак, чтобы определить подчиняется ли рассматриваемое движение закону гармонических колебаний, необходимо уравнение движения привести к виду   и определить   из коэффициента при  . Рассмотрим примеры движения механических систем.

1. Пружинный гармонический маятник (осциллятор)

Г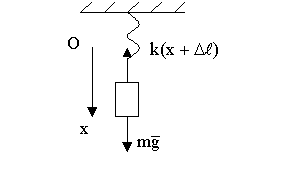 руз (рис. 48) подвешен на невесомой пружине с коэффициентом жесткости  и совершает вертикальные колебания относительно т.   - положения равновесия. По второму закону Ньютона в этом положении

,

где   - растяжение пружины,

а при отклонении из положения равновесия

, т.е.

 

частота и период осциллятора соответственно равны

 и  .

2. Математический маятник

Это идеализированная система, представляющая собой материальную точку с массой  , подвешенную на нерастяжимой нити длиной   и совершающую колебания в вертикальной плоскости (рис. 49).

Опишем движение естественным способом. Точка   отвечает положению равновесия, и тогда

 и соответственно

.

Проекция силы натяжения на касательное направление  , т.е.

 и

.

При малых колебаниях   и

 

,  .

3.Физический маятник

Э то твердое тело, которое совершает колебания вокруг неподвижной оси, жестко связанной с телом.

Рассмотрим колебания под действием силы тяжести (рис. 50). Угол   показывает поворот против часовой стрелки, ось   направлена от плоскости чертежа.

Проекция момента силы тяжести на ось   равна

,

и тогда уравнение динамики вращательного движения принимает вид

,

где   - момент инерции относительно оси O,

 - расстояние между O и центром масс.

При малых колебаниях   и

 

,  .

Здесь   - приведенная длина физического маятника, равная длине математического маятника с такой же  . Если  , то т.  называется центром качания, особенностью которого является, что если маятник перевернуть и колебать относительно  , то   не изменится   принцип определения   с помощью оборотного маятника.

Повторим, что малые поворотные колебания являются гармоническими ввиду того, что действующая в осцилляторе сила квазиупруга, то есть направлена к положению равновесия и зависит от смещения от этого положения линейно, но имеет другую природу, чем упругие силы.

Параметры   и   свободных колебаний без трения зависят от свойств осциллятора;   и   -определяются начальными условиями.

Затухающие колебания. Дифференциальное уравнение затухающих колебаний, его решение и анализ.

Дифференциальное уравнение свободных затухающих колебаний (механических) и его решение. Автоколебания.

Затухающие колебания — колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются.

Закон затухания колебаний определяется свойствами колебательных систем. Обычно рассматривают линейные системы — идеализированные реальные системы, в которых параметры, определяющие физические свойства системы, в ходе процесса не изменяется. Различные по своей природе линейные системы описываются идентичными линейными дифференциальными уравнениями.

Дифференциальное уравнение свободных затухающих колебаний линейной системы

где s — колеблющаяся величина, описывающая тот или иной физический процесс, δ = const — коэффициент затухания, (ω0 — циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при δ =0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы. Решение уравнения рассмотрим в виде

 (7.1) где u=u(t).

После нахождения первой и второй производных и их подстановки в (1) получим

Решение уравнения зависит от знака коэффициента перед искомой величиной. Пусть этот коэффициент положителен:

(7.2)

Тогда получим уравнение решением которого является функция u=A0cos(ωt+φ). Значит, решение уравнения (7.1) в случае малых затуханий

 где 

Период затухающих колебаний с учетом формулы (7.2) равен

 

Если A(t) и A(t+Т) — амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение

называется декрементом затухания, а его логарифм

— логарифмическим декрементом затухания; Ne — число колебаний, совершаемых во время уменьшения амплитуды в е раз. Логарифмический декремент затухания — постоянная для данной колебательной системы величина.

Для характеристики колебательной системы пользуются понятием добротности, которая при малых значениях логарифмического декремента равна

Из формулы следует, что добротность пропорциональна числу колебаний Nе, совершаемых системой за время релаксации.

Для пружинного маятника массой m, совершающего малые колебания под действием упругой силы F=-kx, сила трения пропорциональна скорости, т. е.

где r — коэффициент сопротивления; знак минус указывает на противоположные направления силы трения и скорости.

При данных условиях закон движения маятника будет иметь вид

Используя формулу  и принимая, что коэффициент затухания  получим дифференциальное уравнение затухающих колебаний маятника:

Колебания маятника подчиняются закону

 где частота  

Добротность пружинного маятника

При увеличении коэффициента затухания δ период затухающих колебаний растет и при δ = ω0 обращается в бесконечность, т. е. движение перестает быть периодическим. В данном случае колеблющаяся величина асимптотически приближается к нулю, когда t→∞. Процесс не будет колебательным. Он называется апериодическим.

Вынужденные колебания. Дифференциальное уравнение вынужденных колебаний, его решение и анализ. Явление резонанса.

Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.

Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью какого-либо периодически действующего фактора X(t), изменяющего по гармоническому закону:

Если рассматривать механические колебания, то роль X(t) играет внешняя вынуждающая сила

 (147.1)

С учетом (147.1) закон движения для пружинного маятника (146.9) запишется в виде

 

Используя (142.2) и (146.10), придем к уравнению

  (147.2)

Если рассматривать электрический колебательный контур, то роль X(t) играет подводимая к контуру внешняя периодически изменяющаяся по гармоническому закону э.д.с. или переменное напряжение

  (147.3)

Тогда уравнение (143.2) с учетом (147.3) можно записать в виде

Используя (143.4) и (146.11), придем к уравнению

  (147.4)

Колебания, возникающие под действием внешней периодически изменяющейся силы или внешней периодически изменяющейся э.д.с., называются соответственно вынужденными механическими и вынужденными электромагнитными колебаниями.

Уравнения (147.2) и (147.4) можно свести к линейному неоднородному дифференциальному уравнению

  (147.5)

применяя впоследствии его решение для вынужденных колебаний конкретной физической природы (x0 в случае механических колебаний равно F0/m, в случае электромагнитных — Um/L).

Решение уравнения (147.5) равно сумме общего решения (146.5) однородного уравнения (146.1) и частного решения неоднородного уравнения. Частное решение найдем в комплексной форме (см. § 140). Заменим правую часть уравнения (147.5) на комплексную величину х0 :

  (147.6)

Частное решение этого уравнения будем искать в виде

Подставляя выражение для s и его производных   в уравнение (147.6), получаем

  (147.7)

Так как это равенство должно быть справедливым для всех моментов времени, то время t из него должно исключаться. Отсюда следует, что =w. Учитывая это, из уравнения (147.7) найдем величину s0 и умножим ее числитель и знаменатель на 

Это комплексное число удобно представить в экспоненциальной форме:

где

  (147.8)

   (147.9)

Следовательно, решение уравнения (147.6) в комплексной форме примет вид

Его вещественная часть, являющаяся решением уравнения (147.5), равна

  (147.10)

где А и j задаются соответственно формулами (147.8) и (147.9).

Таким образом, частное решение неоднородного уравнения (147.5) имеет вид

  (147.11)

Решение уравнения (147.5) равно сумме общего решения однородного уравнения

 (147.12)

(см. (146.5)) и частного решения (147.11). Слагаемое (147.12) играет существенную роль только в начальной стадии процесса (при установлении колебаний) до тех пор, пока амплитуда вынужденных колебаний не достигнет значения, определяемого равенством (147.8). Графически вынужденные колебания представлены на рис. 209. Следовательно, в установившемся режиме вынужденные колебания происходят с частотой w и являются гармоническими; амплитуда и фаза колебаний, определяемые выражениями (147.8) и (147.9), также зависят от w.

Запишем формулы (147.10), (147.8) и (147.9) для электромагнитных колебаний, учитывая, что   (см. (143.4)) и   (см. (146.11)):

  (147.13)

Продифференцировав Q=Qmcos(wt–) по t, найдем силу тока в контуре при установившихся колебаниях:

 (147.14)

где

  (147.15)

Выражение (147.14) может быть записано в ввде

где j= – p/2 — сдвиг по фазе между током и приложенным напряжением (см. (147.3)). В соответствии с выражением (147.13)

  (147.16)

Из формулы (147.16) вытекает, что ток отстает по фазе от напряжения (j>0), если L>1/(wС), и опережает напряжение (j<0), если L<1/(wС).

Энергия системы неподвижных точечных зарядов, заряженного проводника, электростатического поля. Объёмная плотность энергии.

 Энергия системы неподвижных точечных зарядов. Как мы уже знаем, электростатические силы взаимодействия консервативны; значит, система зарядов обладает потенциальной энергией. Будем искать потенциальную энергию системы двух неподвижных точечных зарядов Q₁ и Q₂, которые находятся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией (используем формулу потенциала уединенного заряда):    где φ₁₂ и φ₂₁ — соответственно потенциалы, которые создаются зарядом Q₂ в точке нахождения заряда Q₁ и зарядом Q₁ в точке нахождения заряда Q₂. Согласно,   и    поэтому W₁ = W₂ = W и    Добавляя к нашей системе из двух зарядов последовательно заряды Q₃, Q₄, ... , можно доказать, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна   (1)  где φ_i — потенциал, который создается в точке, где находится заряд Q_i, всеми зарядами, кроме i-го.  2. Энергия заряженного уединенного проводника. Рассмотрим уединенный проводник, заряд, потенциал и емкость которого соответственно равны Q, φ и С. Увеличим заряд этого проводника на dQ. Для этого необходимо перенести заряд dQ из бесконечности на уединенный проводник, при этом затратив на это работу, которая равна  ");?>" alt="элементарная работа сил электрического поля заряженного проводника">  Чтобы зарядить тело от нулевого потенциала до φ, нужно совершить работу   (2)  Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник:   (3)  Формулу (3) можно также получить и условия, что потенциал проводника во всех его точках одинаков, так как поверхность проводника является эквипотенциальной. Если φ - потенциал проводника, то из (1) найдем    где Q=∑Q_i - заряд проводника.  3. Энергия заряженного конденсатора. Конденсатор состоит из заряженных проводников поэтому обладает энергией, которая из формулы (3) равна   (4)  где Q — заряд конденсатора, С — его емкость, Δφ — разность потенциалов между обкладками конденсатора.  Используя выражение (4), будем искать механическую (пондеромоторную) силу, с которой пластины конденсатора притягиваются друг к другу. Для этого сделаем предположение, что расстояние х между пластинами изменилось на величину dx. Тогда действующая сила совершает работу dA=Fdx вследствие уменьшения потенциальной энергии системы Fdx = — dW, откуда   (5)  Подставив в (4) выражение для емкости плоского конденсатора, получим   (6)  Продифференцировав при фиксированном значении энергии (см. (5) и (6)), получим искомую силу:    где знак минус указывает, что сила F является силой притяжения.  4. Энергия электростатического поля. Используем выражение (4), которое выражает энергию плоского конденсатора посредством зарядов и потенциалов, и спользуя выражением для емкости плоского конденсатора (C=ε₀εS/d) и разности потенциалов между его обкладками (Δφ=Ed. Тогда   (7)  где V= Sd — объем конденсатора. Формула (7) говорит о том, что энергия конденсатора выражается через величину, характеризующую электростатическое поле, — напряженность Е.  Объемная плотность энергии электростатического поля (энергия единицы объема)   (8)  Выражение (8) справедливо только для изотропного диэлектрика, для которого выполняется соотношение: Р = æε₀Е.  Формулы (4) и (7) соответственно выражают энергию конденсатора через заряд на его обкладках и через напряженность поля. Возникает вопрос о локализации электростатической энергии и что является ее носителем — заряды или поле? Ответ на этот вопрос может дать только опыт. Электростатика занимается изучением постоянных во времени поля неподвижных зарядов, т. е. в ней поля и попродившие их заряды неотделимы друг от друга. Поэтому электростатика ответить на данный вопрос не может. Дальнейшее развитие теории и эксперимента показало, что переменные во времени электрические и магнитные поля могут существовать отдельно, независимо от возбудивших их зарядов, и распространяются в пространстве в виде электромагнитных волн, которые способны переносить энергию. Это убедительно подтверждает основное положение теории близкодействия о том, что энергия локализована в поле и что носителем энергии является поле. 

Постоянный электрический ток и его характеристики: сила тока, плотность тока. Условия существования постоянного тока. Сторонние силы.

В электродинамике — разделе учения об электричестве, в котором рассматриваются явления и процессы, обусловленные движением электрических зарядов или макроскопических заряженных тел, — важнейшим понятием является понятие электрического тока. Электрическим током называется любое упорядоченное (направленное) движение электрических зарядов. В проводнике под действием приложенного электрического поля Е свободные электрические заряды перемещаются: положительные — по полю, отрицательные — против поля (рис. 146, а), т. е. в проводнике возникает электрический ток, называемый током проводимости. Если же упорядоченное движение электрических зарядов осуществляется перемещением в пространстве заряженного макроскопического тела (рис. 146, б), то возникает так называемый конвекционный ток.

Для возникновения и существования электрического тока необходимо, с одной стороны, наличие свободных носителей тока — заряженных частиц, способных перемещаться упорядоченно, а с другой — наличие электрического поля, энергия которого, каким-то образом восполняясь, расходовалась бы на их упорядоченное движение. За направление тока условно принимают направление движения положительных зарядов.

Количественной мерой электрического тока служит сила тока I скалярная физическая величина, определяемая электрическим зарядом, проходящим через поперечное сечение проводника в единицу времени:

Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Для постоянного тока

где Q — электрический заряд, проходящий за время t через поперечное сечение проводника. Единила силы тока — ампер (А).

Физическая величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока, называется плотностью тока:

Выразим силу и плотность тока через скорость vñ упорядоченного движения зарядов в проводнике. Если концентрация носителей тока равна n и каждый носитель имеет элементарный заряд е (что не обязательно для ионов), то за время dt через поперечное сечение S проводника переносится заряд dQ=ne ávñ S dt. Сила тока

а плотность тока

 (96.1)

Плотность тока — вектор, ориентированный по направлению тока, т. е. направление вектора j совпадает с направлением упорядоченного движения положительных зарядов. Единица плотности тока — ампер на метр в квадрате (А/м2).

Сила тока сквозь произвольную поверхность S определяется как поток вектора j, т. е.

  (96.2)

где dS=ndS (n — единичный вектор нормали к площадке dS, составляющей с вектором j угол a).

Сторонние силы. Электродвижущая сила и напряжение

Если в цепи на носители тока действуют только силы электростатического поля, то происходит перемещение носителей (они предполагаются положительными) от точек с большим потенциалом к точкам с меньшим потенциалом. Это приведет к выравниванию потенциалов во всех точках цепи и к исчезновению электрического поля. Поэтому для существования постоянного тока необходимо наличие в цепи устройства, способного создавать и поддерживать разность потенциалов за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками тока. Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними.

Природа сторонних сил может быть различной. Например, в гальванических элементах они возникают за счет энергии химических реакций между электродами и электролитами; в генераторе — за счет механической энергии вращения ротора генератора и т. п. Роль источника тока в электрической цепи, образно говоря, такая же, как роль насоса, который необходим для перекачивания жидкости в гидравлической системе. Под действием создаваемого поля сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему на концах цепи поддерживается разность потенциалов и в цепи течет постоянный электрический ток.

Сторонние силы совершают работу по перемещению электрических зарядов. Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называется электродвижущей силой (э.д.с.), действующей в цепи:

  (97.1)

Эта работа производятся за счет энергии, затрачиваемой в источнике тока, поэтому величину   можно также называть электродвижущей силой источника тока, включенного в цепь. Часто, вместо того чтобы сказать: «в цепи действуют сторонние силы», говорят: «в цепи действует э.д.с.», т. е. термин «электродвижущая сила» употребляется как характеристика сторонних сил. Э.д.с., как и потенциал, выражается в вольтах (ср. (84.9) и (97.1)).

Сторонняя сила Fст, действующая на заряд Q0, может быть выражена как

где Е — напряженность поля сторонних сил. Работа же сторонних сил по перемещению заряда Q0 на замкнутом участке цепи равна

  (97.2)

Разделив (97.2) на Q0, получим выражение для э. д. с., действующей в цепи:

т. е. э.д.с., действующая в замкнутой цепи, может быть определена как циркуляция вектора напряженности поля сторонних сил. Э.д.с., действующая на участке 1—2, равна

  (97.3)

На заряд Q0 помимо сторонних сил действуют также силы электростатического поля Fe=Q0E. Таким образом, результирующая сила, действующая в цепи на заряд Q0, равна

Работа, совершаемая результирующей силой над зарядом Q0 на участке 1—2, равна

Используя выражения (97.3) и (84.8), можем записать

  (97.4)

Для замкнутой цепи работа электростатических сил равна нулю (см. § 83), поэтому в данном случае 

Напряжением U на участке 1—2 называется физическая величина, определяемая работой, совершаемой суммарным полем электростатических (кулоновских) и сторонних сил при перемещении единичного положительного заряда на данном участке цепи. Таким образом, согласно (97.4),

Понятие напряжения является обобщением понятия разности потенциалов: напряжение на концах участка цепи равно разности потенциалов в том случае, если на этом участке не действует Э.д.с., т. е. сторонние силы отсутствуют.

Магнитное поле в вакууме. Циркуляция вектора магнитной индукции. Закон полного тока. Ротор магнитного поля. Вычисление магнитного поля соленоида и тороида Действие магнитного поля на движущийся заряд. Сила Лоренца. Действие магнитного поля на проводник с током. Сила Ампера. Взаимодействие параллельных токов. Ампер - единица СИ. Действие магнитного поля на проводящий контур с постоянным током. Работа получаемая при перемещении проводника с током в магнитном поле. Эффект Холла. 

Обобщённый закон Ома в интегральной форме. Разность потенциалов, ЭДС, напряжение.

http://physics-lectures.ru/postoyannyj-elektricheskij-tok/17-4-zakon-oma-v-integralnoj-forme/

закон Ома в интегральной форме.

Потенциал электростатического поля — скалярная величина, равная отношению потен­циальной энергии заряда в поле к этому заряду:   

Разность потенциалов

Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних (непотенциальных) сил в источникахпостоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительногозаряда вдоль контура.

Электри́ческое напряже́ние между точками A и B электрической цепи или электрического поля — физическая величина, значение которой равно отношению работы электрического поля, совершаемой при переносе пробного электрического заряда из точки A в точку B, к величине пробного заряда.

Основные положения классической электронной теории электропроводимости металлов. Вывод закона Ома и Джоуля-Ленца в дифференциальной форме из электронных представлений.

Основные положения этой теории сводятся к следующим:

1). Носителями тока в металлах являются электроны, движение которых подчиняется законом классической механики.

2). Поведение электронов подобно поведению молекул идеального газа (электронный газ).

3). При движении электронов в кристаллической решетке можно не учитывать столкновения электронов друг с другом.

4). При упругом столкновении электронов с ионами электроны полностью передают им накопленную в электрическом поле энергию.

Средняя тепловая скорость хаотического движения электронов при Т≈300Ксоставляет  .

При включении электрического поля на хаотическое движение электронов накладывается упорядоченное движение (называемое иногда «дрейфовым»),происходящее с некоторой средней скоростью  ; возникает направленное движение электронов – электрический ток. Плотность тока определяется по формуле .

Оценки показывают, что при максимально допустимой плотности тока в металлах j = 10⁷ А/м² и концентрации носителей 10²⁸ – 10²⁹м^-3 ,  . Таким образом, даже при очень больших плотностях тока средняя скорость упорядоченного движения электронов  .

К концу свободного пробега электрон приобретает скорость   , и, следовательно, дополнительную кинетическую энергию, средняя величина которой

Столкнувшись с ионом, электрон по предположению полностью теряет приобретенную им за время пробега скорость, и передает энергию кристаллической решетке. Эта энергия идет на увеличение внутренней энергии металла, проявляющееся в его нагревании. Каждый электрон претерпевает за секунду в среднем 1/t соударений, сообщая всякий раз решетке энергию   . Следовательно, в единице объема за единицу времени должно выделяться тепло

где n - число электронов проводимости в единице объема. Величина   есть не что иное, как удельная мощность тока. Множитель при   совпадает со значением   (18.3) для закона Ома. Таким образом. Мы пришли к выражению закона Джоуля-Ленца в дифференциальной форме.

Друде считал, что сразу после очередного соударения электрона с ионом кристаллической решетки скорость упорядоченного движения электрона равна нулю. Предположим, что напряженность поля не изменяется. Тогда под действием поля электрон получит постоянное ускорение равное

и к концу пробега скорость упорядоченного движения достигнет значения

(18.2)

где t - среднее время между двумя последовательными соударениями электрона с ионами решетки. Друде не учитывал распределение электронов по скоростям и приписывал всем электронам одинаковое значение средней скорости   . В этом приближении   , где   - среднее значение длины свободного пробега,   - скорость теплового движения электронов. Подставим это значение t в формулу (18.2)

Скорость изменяется за время пробега линейно. Поэтому ее среднее (за пробег) значение равно половине максимального

Подставив это выражение в

получим

Плотность тока оказалась пропорциональной напряженности поля. Следовательно, мы получили закон Ома. Согласно   коэффициент пропорциональности между j и Е представляет собой проводимость

(18.3)

Если бы электроны не сталкивались с ионами решетки, длина свободного пробега, а, следовательно, и проводимость были бы бесконечно велики. Таким образом, электрическое сопротивление металлов обусловлено соударениями свободных электронов с ионами.

Работа выхода, контактная разность потенциалов, явление Зеебека и Пельтье

Свободные электроны металла движутся по кристаллической решетке хаотически с огромными скоростями  . В целом металл электрически нейтрален. Если бы его потенциал был равен потенциалу окружающей среды (вакуума), то ничто не препятствовало бы вылету свободных электронов за пределы металла. В действительности на границе проводника создается эффективное электрическое поле, препятствующее такому вылету. Металл окружен очень тонким отрицательно заряженным слоем электронов, а ионы на границе металла образуют слой положительного заряда той же величины. Такое распределение заряда на границе металла создает двойной электрический слой, толщина которого не превышает нескольких межатомных расстояний.

Электрическое поле   двойного слоя препятствует вылету свободных электронов в вакуум. Энергия электрона   за пределами металла, в вакууме, больше, чем внутри металла, а для потенциалов электрического поля на границе выполняется условие  . Чтобы электрон вылетел из металла, ему надо совершить работу против сил этого граничного электрического поля и приобрести энергию     Величина   называется потенциалом выхода электрона из металла.

Работой выхода электрона из металла называется минимальная энергия, которую надо сообщить электрону в металле, чтобы он преодолел поле двойного электрического слоя и вылетел за пределы металла: . Контактная разность потенциалов

Металлы различаются значениями концентрации свободных электронов n, работой выхода и величиной энергии Ферми  . Чем больше концентрация свободных электронов, тем большую величину имеет энергия Ферми, и тем меньше работа выхода электрона из металла.

Если металлы соединить, то начнется диффузия свободных электронов из металла, в котором их концентрация больше, в металл, где она меньше. Эта диффузия продолжаться до тех пор, пока концентрации свободных электронов в металлах не сравняются. Наступает динамическое равновесие: сколько электронов переносится через границу за счет диффузии, столько же и возвращается обратно электрическим  полем в месте контакта. При контакте, в состоянии  динамического равновесия, энергии Ферми (средние энергии свободных электронов) в обоих металлах выравниваются, Хотя потенциалы металлов постоянны (j1=const, j2=const), но они не равны между собой. Их разность   называется контактной разностью потенциалов.

Контактная  разность потенциалов имеет не электростатическую природу (возникает за счет диффузии) и является электродвижущей силой, способной создать ток. Но если спаять в кольцо проводники из разных металлов, то возникающие в контакте э.д.с. направлены навстречу друг другу и компенсируются: ток по такой замкнутой цепи не потечет.

Эффект Зеебека — явление возникновения ЭДС в замкнутой электрической цепи, состоящей из последовательно соединённых разнородных проводников, контакты между которыми находятся при различных температурах.

Эффект Зеебека состоит в том, что в замкнутой цепи, состоящей из разнородных проводников, возникает термо-ЭДС, если места контактов поддерживают при разных температурах. Цепь, которая состоит только из двух различных проводников, называется термоэлементом или термопарой.

Величина возникающей термоэдс в первом приближении зависит только от материала проводников и температур горячего ( ) и холодного ( ) контактов.

В небольшом интервале температур термоэдс   можно считать пропорциональной разности температур:

 где   — термоэлектрическая способность пары (или коэффициент термоэдс).

В простейшем случае коэффициент термоэдс определяется только материалами проводников, однако, строго говоря, он зависит и от температуры, и в некоторых случаях с изменением температуры   меняет знак.

Более корректное выражение для термоэдс:

Величина термоэдс составляет милливольты при разности температур в 100 К и температуре холодного спая в 0 °С (например, пара медь-константан даёт 4,25 мВ, платина-платинородий — 0,643 мВ, нихром-никель — 4,1 мВ)^[2].

Эффект Пельтье — термоэлектрическое явление, при котором происходит выделение или поглощение тепла при прохождении электрического тока в месте контакта (спая) двух разнородных проводников. Величина выделяемого тепла и его знак зависят от вида контактирующих веществ, направления и силы протекающего электрического тока:

Q = П_АBIt = (П_B-П_A)It, где

Q — количество выделенного или поглощённого тепла;

I — сила тока;

t — время протекания тока;

П — коэффициент Пельтье, который связан с коэффициентом термо-ЭДС α вторым соотношением Томсона ^[1] П = αT, где Т — абсолютная температура в K.

Магнитное поле и его характеристики: индукция, напряжённость, закон Ампера.

Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения^[1], магнитная составляющая электромагнитного поля^[2]

Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах 

Магни́тная инду́кция   — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой   магнитное поле действует на заряд  , движущийся со скоростью  .

Более конкретно,   — это такой вектор, что сила Лоренца  , действующая со стороны магнитного поля^[1] на заряд  , движущийся со скоростью  , равна

Напряжённость магни́тного по́ля (стандартное обозначение Н) — векторная физическая величина, равная разности вектора магнитной индукции B ивектора намагниченности M.

В СИ:   где   — магнитная постоянная.

Закон Ампера устанавливает, что на проводник с током, помещенный в однородное магнитное поле, индукция которого В, действует сила, пропорциональная силе тока и индукции магнитного поля:

F = BIlsina (a - угол между направлением тока и индукцией магнитного поля ). Эта формула закона Ампера оказывается справедливой для прямолинейного проводника и однородного поля.

Если проводник имеет произвольную формулу и поле неоднородно, тоЗакон Ампера принимает вид:

dF = I*B*dlsina

Закон Ампера в векторной форме:

dF = I [dl B]

Сила Ампера направлена перпендикулярно плоскости, в которой лежат векторы dl и B.

Для определения направления силы, действующей на проводник с током, помещенный в магнитное поле, применяется правило левой руки.

Контур с током в магнитном поле.

Рис. 4.13

Пусть в однородное магнитное поле помещена рамка с током (рис. 4.13). Тогда силы Ампера, действующие на боковые стороны рамки, будут создавать вращающий момент, величина которого пропорциональна магнитной индукции, силе тока в рамке, ее площади S и зависит от угла a между вектором   и нормалью к площади  :

.

Направление нормали выбирают так, чтобы в направлении нормали перемещался правый винт при вращении по направлению тока в рамке.

Максимальное значение вращательный момент имеет тогда, когда рамка устанавливается перпендикулярно магнитным силовым линиям:

.

Это выражение также можно использовать для определения индукции магнитного поля:

.

Величину, равную произведению  , называют магнитным моментом контура Р_т. Магнитный момент есть вектор, направление которого совпадает с направлением нормали к контуру. Тогда вращательный момент можно записать

.

При угле a = 0 вращательный момент равен нулю. Значение вращательного момента зависит от площади контура, но не зависит от его формы. Поэтому на любой замкнутый контур, по которому течет постоянный ток, действует вращательный момент М, который поворачивает его так, чтобы вектор магнитного момента установился параллельно вектору индукции магнитного поля.

Закон Био-Савара-Лапласа и его применение к вычислению магнитных полей прямолинейного проводника с током и кругового момента.

 Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к вам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол  (угол между векторами dl и r), выразив через него все остальные величины. Из рис. 165 следует, что

(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна

                                                       (110.4)

Так как угол   для всех элементов прямого тока изменяется в пределах от 0 до , то, согласно (110.3) и (110.4),

Следовательно, магнитная индукция поля прямого тока

Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sin =1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),

Тогда

Следовательно, магнитная индукция поля в центре кругового проводника с током

Теорема о циркуляции вектора магнитной индукции(закон полного тока). Вихревой характер магнитного поля. Применение теоремы о циркуляции к расчёту магнитных полей.

Закон полного тока это закон, связывающий циркуляцию вектора напряженности магнитного поля и ток.

Циркуляция вектора напряженности магнитного поля по контуру равна алгебраической сумме токов, охватываемых этим контуром.

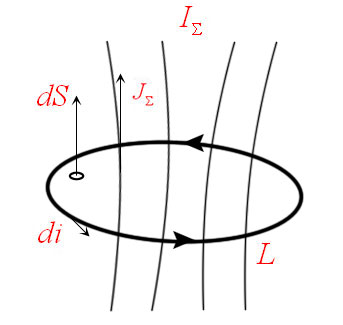
Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток протоивоположного направления считается отрицательным.

Линии магнитной индукции непрерывны: они не имеют ни начала, ни конца. Это имеет место для любого магнитного поля, вызванного какими угодно контурами с током. Векторные поля, обладающие непрерывными линиями, получили название вихревых полей. Мы видим, что магнитное поле есть вихревое поле. В этом заключается существенное отличие магнитного поля от электростатического.

Примеры применения теоремы о циркуляции для расчета магнитных полей

1. Расчет магнитного поля соленоида

Соленоид – проводник, навитый по винтовой линии на поверхность цилиндра (рис.45).

П усть по проводнику течет ток  . Направление вектора   образует с направлением тока правовинтовую систему внутри соленоида. Обозначим   – число витков на единицу длины.

Cчитая шаг малым, можно заменить витки круговыми, замкнутыми. Пусть сечение проводника мало, т.е. ток считаем текущим по поверхности.

Из опыта и из расчета   при увеличении длины соленоида вектор   снаружи уменьшается, значит, снаружи бесконечно длинного соленоида поля нет.

И з симметрии   вектор   направлен вдоль оси (линии вектора   параллельны, и поле внутри однородно).

Контур выбираем таким образом, чтобы вдоль него вектор   был одинаков (рис.46).

По теореме о циркуляции

,

где   - циркуляция,

 - ток, охватываемый данным контуром,

 – число ампервитков.

Тогда

- внутри соленоида поле однородно (без учета краевых эффектов).

2. Расчет магнитного поля тороида

Тороид – проводник, навитый на поверхность в виде тора.

Обозначим (рис.47)

 – радиус тора,

 – радиус контура;

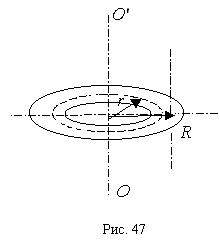 – число витков.

Из симметрии 

линии вектора  - окружности, центры, которых лежат на оси   

в качестве контура берем такую окружность.

Если контур - внутри тороида: он охватывает ток  , и по теореме о циркуляции

,

 .

При   и     формула для бесконечно длинного соленоида.

Вне тороида: контур токов не охватывает:  , магнитного поля нет.

У реального тороида линии тока (витки) не находятся в плоскости, проходящей через ось   (как принималось в расчете)   имеется дополнительная составляющая тока вдоль оси, создающая поле, аналогичное полю кругового тока.

Теорема о циркуляции вектора   используется в редких случаях (например, для такой симметричной конфигурации как круговой виток, теорему использовать нецелесообразно, т. к. нельзя выбрать простой контур).

Выбор контура (такого, где  =const) – основной этап решения задач в этом направлении.

Понятие о магнитном потоке. Работа перемещения проводника и контура с током в магнитном поле.

В однородном магнитном поле, модуль вектора индукции которого равен В, помещен плоский замкнутый контур площадью S. Нормаль n к плоскости контура составляет угол a с направлением вектора магнитной индукции В.

Магнитным потоком через поверхность называется величина Ф, определяемая соотношением:

Φ = B · S · cos α

Единица измерения магнитного потока в систем СИ - 1 Вебер (1 Вб).

1 Вб = 1 Тл · 1 м²

На проводник с током в магнитном поле действуют силы, которые определяются с помощью закона Ампера. Если проводник не закреплен (например, одна из сторон контура сделана в виде подвижной перемычки, рис. 1), то под действием силы Ампера он в магнитном поле будет перемещаться. Значит, магнитное поле совершает работу по перемещению проводника с током.  Для вычисления этой работы рассмотрим проводник длиной l с током I (он может свободно двигаться), который помещен в однородное внешнее магнитное поле, которое перпендикулярно плоскости контура. Сила, направление которой определяется по правилу левой руки, а значение — по закону Ампера, рассчитывается по формуле    Под действием данной силы проводник передвинется параллельно самому себе на отрезок dx из положения 1 в положение 2. Работа, которая совершается магнитным полем, равна    так как ldx=dS — площадь, которую пересекает проводник при его перемещении в магнитном поле, BdS=dФ — поток вектора магнитной индукции, который пронизывает эту площадь. Значит,   (1)  т. е. работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником. Данная формула справедлива и для произвольного направления вектора В.  Рассчитаем работу по перемещению замкнутого контура с постоянным током I в магнитном поле. Будем считать, что контур М перемещается в плоскости чертежа и в результате бесконечно малого перемещения перейдет в положение М', изображенное на рис. 2 штриховой линией. Направление тока в контуре (по часовой стрелке) и магнитного поля (перпендикулярно плоскости чертежа — за чертеж или от нас) дано на рисунке. Контур М условно разобьем на два соединенных своими концами проводника: AВС и CDА.  Работа dA, которая совершается силами Ампера при иссследуемом перемещении контура в магнитном поле, равна алгебраической сумме работ по перемещению проводников AВС (dA₁) и CDA (dA₂), т. е.   (2)  Силы, которые приложенны к участку CDA контура, образуют острые углы с направлением перемещения, поэтому совершаемая ими работа dA₂>0. .Используя (1), находим, эта работа равна произведению силы тока I в нашем контуре на пересеченный проводником CDA магнитный поток. Проводник CDA пересекает при своем движении поток dФ₀ сквозь поверхность, выполненную в цвете, и поток dФ₂, который пронизывает контур в его конечном положении. Значит,   (3)  Силы, которые действуют на участок AВС контура, образуют тупые углы с направлением перемещения, значит совершаемая ими работа dA₁<0. Проводник AВС пересекает при своем движении поток dФ₀ сквозь поверхность, выполненную в цвете, и поток dФ1, который пронизывает контур в начальном положении. Значит,   (4)  Подставляя (3) и (4) в (2), найдем выражение для элементарной работы:    где dФ₂—dФ₁=dФ' — изменение магнитного потока сквозь площадь, которая ограничена контуром с током. Таким образом,   (5)  Проинтегрировав выражение (5), найдем работу, которая совершается силами Ампера, при конечном произвольном перемещении контура в магнитном поле:   (6)  значит, работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром. Выражение (6) верно для контура любой формы в произвольном магнитном поле. 

Эффект Холла и его применение. МГД-генератора.

Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле.

В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле  течёт электрический ток под действием напряжённости  . Магнитное поле будет отклонять носители заряда (для определённостиэлектроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости^[1] будет служить условие, что при этом электрон не начнёт двигаться по циклоиде.

Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов   не скомпенсирует магнитную составляющую силы Лоренца:

Скорость электронов   можно выразить через плотность тока:

где   — концентрация носителей заряда. Тогда

Коэффициент   пропорциональности между   и   называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как свинец, цинк, железо, кобальт, вольфрам), в сильных полях наблюдается положительный знак  , что объясняется в полуклассической и квантовой теориях твёрдого тела.

Эффект Холла, в некоторых случаях, позволяет определить тип носителей заряда (электронный или дырочный) в металле или полупроводнике, что делает его достаточно хорошим методом исследования свойств полупроводников.

На основе эффекта Холла работают датчики Холла: приборы, измеряющие напряжённость магнитного поля. Датчики Холла получили очень большое распространение в бесколлекторных, или вентильных, электродвигателях (сервомоторах). Датчики закрепляются непосредственно на статоре двигателя и выступают в роли ДПР (датчика положения ротора). ДПР реализует обратную связь по положению ротора, выполняет ту же функцию, что и коллектор в коллекторном ДПТ.

Также на основе эффекта Холла работают некоторые виды ионных реактивных двигателей.

Явление электромагнитной индукции. Закон Фарадея и его выводы из электронных представлений.

Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.

Согласно закону электромагнитной индукции Фарадея (в СИ):

где

 — электродвижущая сила, действующая вдоль произвольно выбранного контура,

   — магнитный поток через поверхность, натянутую на этот контур.

Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца:

Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:

где

 — электродвижущая сила,

 — число витков,

 — магнитный поток через один виток,

 — потокосцепление катушки.

Индуктивность соленоида. Явление самоиндукции. Токи при замыкании и размыкании цепи. Энергия магнитного поля.

Индуктивность соленоида выражается следующим образом:

 (СИ),

 (СГС),

где   — объём соленоида,   — длина проводника, намотаннного на соленоид,   — длина соленоида,   — диаметр витка.

Без использования магнитного материала плотность магнитного потока   в пределах катушки является фактически постоянной и равна

где   − магнитная проницаемость вакуума,   − число витков,   — сила тока и   — длина катушки. Пренебрегая краевыми эффектами на концах соленоида, получим, чтопотокосцепление через катушку равно плотности потока  , умноженному на площадь поперечного сечения   и число витков  :

Отсюда следует формула для индуктивности соленоида

 эквивалентная предыдущим двум формулам.

Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре ^[1]при изменении протекающего через контур тока.

При изменении тока в контуре пропорционально меняется^[2] и магнитный поток через поверхность, ограниченную этим контуром^[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.

Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока  :

.

 По правилу Ленца дополнительные токи, возникающие в проводниках вследствие самоиндукции, всегда направлены так, чтобы воспрепятствовать изменениям тока, текущего в цепи. Это приводит к тому, что установление тока при замыкании цепи и убывание тока при размыкании цепи происходит не мгновенно, а постепенно.

Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии.

Энергия W_м магнитного поля катушки с индуктивностью L, создаваемого током I, равна

                                      W_м = LI²/ 2

Описание магнитного поля в веществе. Классификация материалов по магнитным свойствам.

Классификация магнитных материалов по магнитным свойствам

В зависимости от магнитных свойств материалы разделяют на диамагнетики, парамагнетики, ферромагнетики. Количественно магнитные свойства материалов принято оценивать по их магнитной восприимчивости λ = М/Н, где М — намагниченность вещества; Н — напряженность магнитного поля.

Диамагнетики

Это вещества, атомы, ионы или молекулы которых не имеют результирующего магнитного момента при отсутствии внешнего поля. Диамагнитный эффект является результатом воздействия внешнего магнитного поля на молекулярные токи и проявляется в том, что возникает магнитный момент, направленный в сторону, обратную внешнему полю. Таким образом, во внешнем магнитном поле диамагнетики намагничиваются противоположно приложенному полю, т. е. имеют отрицательную магнитную восприимчивость (λ < 0). Диамагнитные вещества выталкиваются из неравномерного магнитного поля, а в равномерном магнитном поле вектор намагниченности диамагнетика стремится расположиться перпендикулярно к направлению поля. Диамагнетизм присущ всем без исключения веществам в твердом, жидком и газообразном состояниях, но проявляется слабо и часто подавляется другими эффектами.

Парамагнетики

Это вещества, атомы, ионы или молекулы которых имеют результирующий магнитный момент при отсутствии внешнего магнитного поля. Во внешнем магнитном поле парамагнетики намагничиваются согласно с внешним полем, т. е. имеют положительную магнитную восприимчивость (λ > 0). Парамагнитный эффект присущ веществам с нескомпенсированным магнитным моментом атомов при отсутствии у них порядка в ориентации этих моментов. Поэтому, когда нет внешнего магнитного поля, атомные магнитные моменты располагаются хаотически и намагниченность парамагнитного вещества равна нулю. При воздействии внешнего магнитного поля атомные магнитные моменты получают преимущественную ориентацию в направлении этого поля, и у парамагнитного вещества проявляется намагниченность.

Ферромагнетики

Это вещества, в которых магнитные моменты атомов или ионов находятся в состоянии самопроизвольного магнитного упорядочения, причем результирующие магнитные моменты каждого из доменов отличны от нуля. При воздействии внешнего магнитного поля магнитные моменты доменов приобретают преимущественное ориентирование в направлении этого поля и ферромагнитное вещество намагничивается. Ферромагнитные вещества характеризуются большим значением магнитной восприимчивости (>> 1), а также ее нелинейной зависимостью от напряженности магнитного поля и температуры, способностью намагничиваться до насыщения при обычных температурах даже в слабых магнитных полях, гистерезисом — зависимостью магнитных свойств от предшествующего магнитного состояния, точкой Кюри, т. е. температурой, выше которой материал теряет ферромагнитные свойства. К ферромагнитным веществам относятся железо, никель, кобальт, их соединения и сплавы, а также некоторые сплавы марганца, серебра, алюминия. Ферромагнитные свойства у вещества могут возникать лишь при достаточно большом значении обменного взаимодействия, что характерно для кристаллов железа, кобальта, никеля и др. Необходимое значение обменного взаимодействия ферромагнетики имеют лишь в твердом состоянии. Этим объясняется отсутствие в природе жидких и газообразных ферромагнетиков. Ферромагнетизм сплавов, целиком состоящих из «парамагнитных» компонентов, объясняется тем, что в этих сплавах, основой которых обычно является марганец или хром, введение в решетку основы атомов висмута, сурьмы, серы и теллура изменяет электронную структуру кристаллов, в результате чего создаются условия для возникновения ферромагнетизма.

Диамагнетики. Электронная теория диамагнетизма.

Диамагнетизм - один из видов магнетизма; проявляется в намагничивании вещества навстречу направлению действующего на него внешнего магнитного поля.

Д. свойствен всем веществам. При внесении какого-либо тела в магнитное поле в электронной оболочке каждого его атома, в силу закона электромагнитной индукции, возникают индуцированные круговые токи, т. е. добавочное круговое движение электронов вокруг направления магнитного поля. Эти токи создают в каждом атоме индуцированный магнитный момент, направленный, согласно правилу Ленца, навстречу внешнему магнитному полю (независимо от того, имелся ли первоначально у атома собственный магнитный момент или нет и как он был ориентирован). В веществе Д. может перекрываться в большей или меньшей степени электронным или ядерным парамагнетизмом, ферромагнетизмом или антиферромагнетизмом. У чисто диамагнитных веществ электронные оболочки атомов (молекул) не обладают постоянным магнитным моментом. Магнитные моменты, создаваемые отдельными электронами в таких атомах, в отсутствие внешнего магнитного поля взаимно скомпенсированы. В частности, это имеет место в атомах, ионах и молекулах с целиком заполненными электронными оболочками, например в атомах инертных газов, в молекулах водорода, азота.

Парамагнетики. Классическая теория Ланжевена.

Парамагнетики - это вещества, намагничивающиеся во внешнем магнитном поле по направлению поля (например редкоземельные металлы, Pt, Al).

У парамагнетиков при отсутствии внешнего магнитного поля магнитные моменты электронов не компенсируют друг друга, и молекулыпарамагнетиков всегда обладают магнитным моментом (такие молекулы называются полярными).

Вследствие теплового движения молекул их магнитные моменты ориентированы беспорядочно, поэтому в отсутствие магнитного поля,парамагнетики магнитными свойствами не обладают.

При внесении парамагнетика во внешнее магнитное поле устанавливается преимущественная ориентация магнитных моментов атомов (молекул) по полю (полной ориентации препятствует тепловое движение атомов).

Таким образом, парамагнетики намагничиваются, создавая собственное магнитное поле, совпадающее по направлению с внешним полем и усиливающим его. Этот эффект называется парамагнитным. Если магнитный момент атомов (молекул) велик, то парамагнитные свойства преобладают над диамагнитными и вещество является парамагнетиком.

Теория парамагнетизма строится так же, как теория ориента-ционной электрической поляризации: под действием внешнего магнитного поля магнитные дипольные моменты ориентируются по направлению поля, а тепловое движение оказывает на них дезориентирующее действие; в результате устанавливается некоторая равновесная магнитная поляризация вещества.

Ферромагнетики, их основные свойства. Доменная природа феромагнетизма.

Ферромагнетики — вещества (как правило, в твёрдом кристаллическом или аморфном состоянии), в которых ниже определённой критическойтемпературы (точки Кюри) устанавливается дальний ферромагнитный порядок магнитных моментов атомов или ионов (в неметаллических кристаллах) или моментов коллективизированных электронов (в металлических кристаллах). Иными словами, ферромагнетик — такое вещество, которое, при температуре ниже точки Кюри, способно обладать намагниченностью в отсутствие внешнего магнитного поля.