Геометрия зацепления колес.

Роль начальных и делительных цилиндров цилиндрических зубча­тых передач в конических передачах играют начальные и делитель­ные конусы. При вращении колес начальные конусы катятся друг по другу без скольжения (рис. 3.21). В конических передачах угловая коррекция не применяется, поэтому начальные и делительные конусы

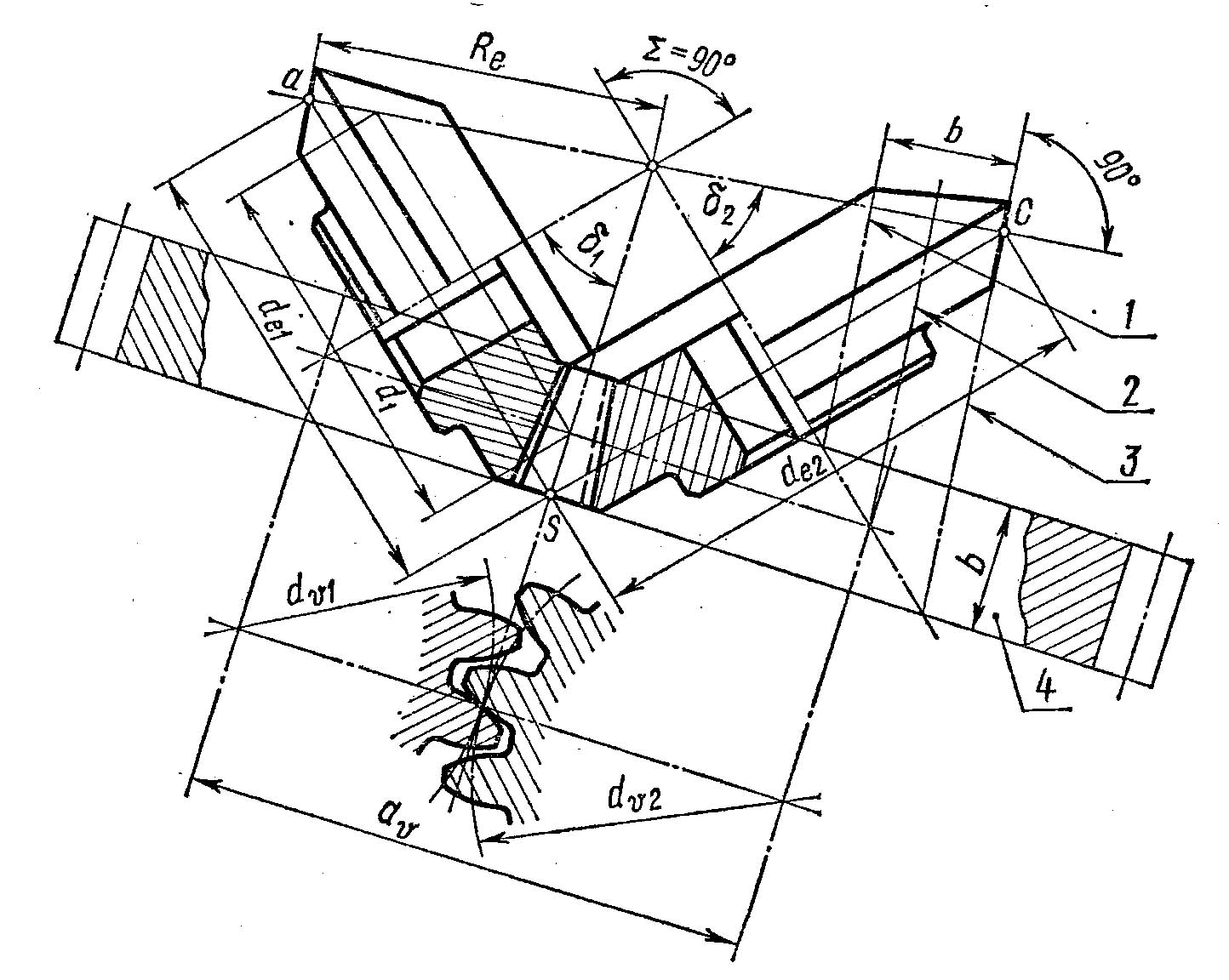
Рис. 3.21. Схема к геометрии зацепления конических колес:

1, 2, 3 - образующие внутреннего, среднего и внешнего дополнительных конусов;

4 - эквивалентное колесо.

всегда совпадают. Углы делительных конусов обозначают соответст­венно δ₁ и δ₂. Угол между осями ∑=δ₁+δ₂. Эвольвентные зубья конического колеса профилируют на развертке дополнительного конуса, образующая которого перпендикулярна образующей дели­тельного конуса. Дополнительные конусы можно построить для внеш­него, среднего и внутреннего сечений конического колеса. Ширина венца зубчатого колеса b ограничена двумя дополнительными кону­сами — внешним и внутренним.

Передаточное отношение.

Аналогично конической фрикционной передаче при ∑=90° передаточное отношение:

i=ω1/ω2=de2/de1=tg δ2=1/tg δ1

где d_e1 и d_e2 - внешние делительные диаметры колес. Передаточное число: u=z₂/z₁

Для конической прямозубой передачи рекомендуется u=2—3; при колесах с непрямыми зубьями возможны более высокие значе­ния u; наибольшее значение u= 6,3 (ГОСТ 12289-76).

Основные геометрические соотношения.

Как известно, модуль зубьев представляет собой отношение диа­метра делительной окружности к числу зубьев колеса, но для делитель­ного конуса конического зубчатого колеса этих диаметров, а следова­тельно, и модулей бесчисленное множество. При разных по длине зуба модулях высота зуба также величина переменная. Для удобства измерения размеры конических колес принято опреде­лять по внешнему торцу зуба, образованному внешним дополнительным конусом. Максимальный модуль зубьев m_e - внешний

Р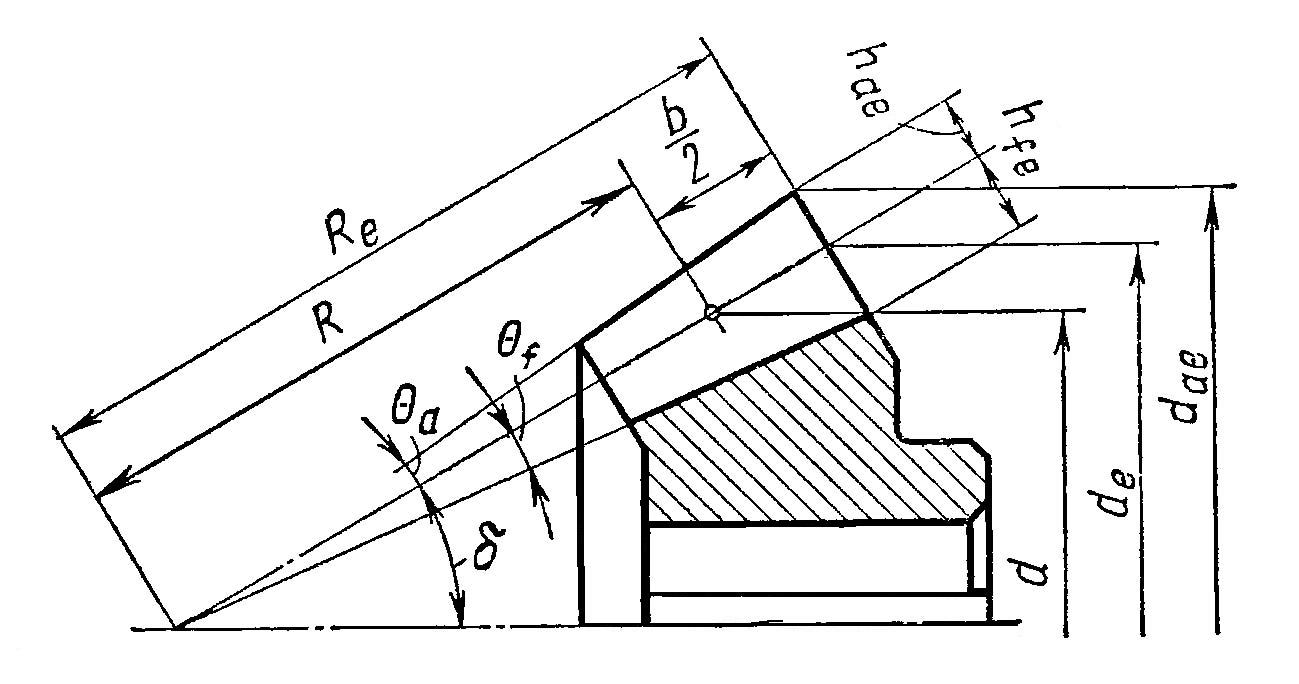 ис. 3.22. К геометрическому расчету конического колеса.

окружной модуль, полученный по внешнему торцу, иногда называют производственным модулем. Его обычно ок­ругляют по ГОСТ 9563-60. Внешний делительный диаметр: d_e=m_ez.

Для нормального (некорригированного) зацепления высоты го­ловки зуба h_ae и ножки h_fe соответственно равны:

hae=me; hfe=1,2me

Внешний диаметр вершин зубьев:

dae=de+2me cosδ

Внешнее конусное расстояние:

или

Среднее конусное расстояние:

R=Re-0,5b

Угол ножки зуба:

tgΘf=hfe/Re

По ГОСТ 19624-74 Θ_a1=Θ_f2; Θ_a2=Θ_f1, здесь Θ_a - угол го­ловки зуба.

Средний делительный диаметр шестерни:

где b - ширина венца колес.

Разделив на z₁ левую и правую части формулы, получим средний модуль зубьев

m=me-(bsinδ1)/z1

Силы в конической прямозубой передаче определяют по размерам средних сечений зубьев, в которых лежит точка приложения силы F_n, действующей перпендикулярно к поверхности зуба (рис.). Раз­ложив Fn на составляющие, получим:

окружную силу на шестерне:

Ft1=2T1/d1

радиальную силу на шестерне:

Fr1=Ft1tgwcosδ1

осевую силу на шес­терне:

Fa1=Ft1tgwsinδ1

Силы на колесе по вели­чине соответственно равны:

Ft2=Ft1; Fr2=Fa1; Fa2=Fr1

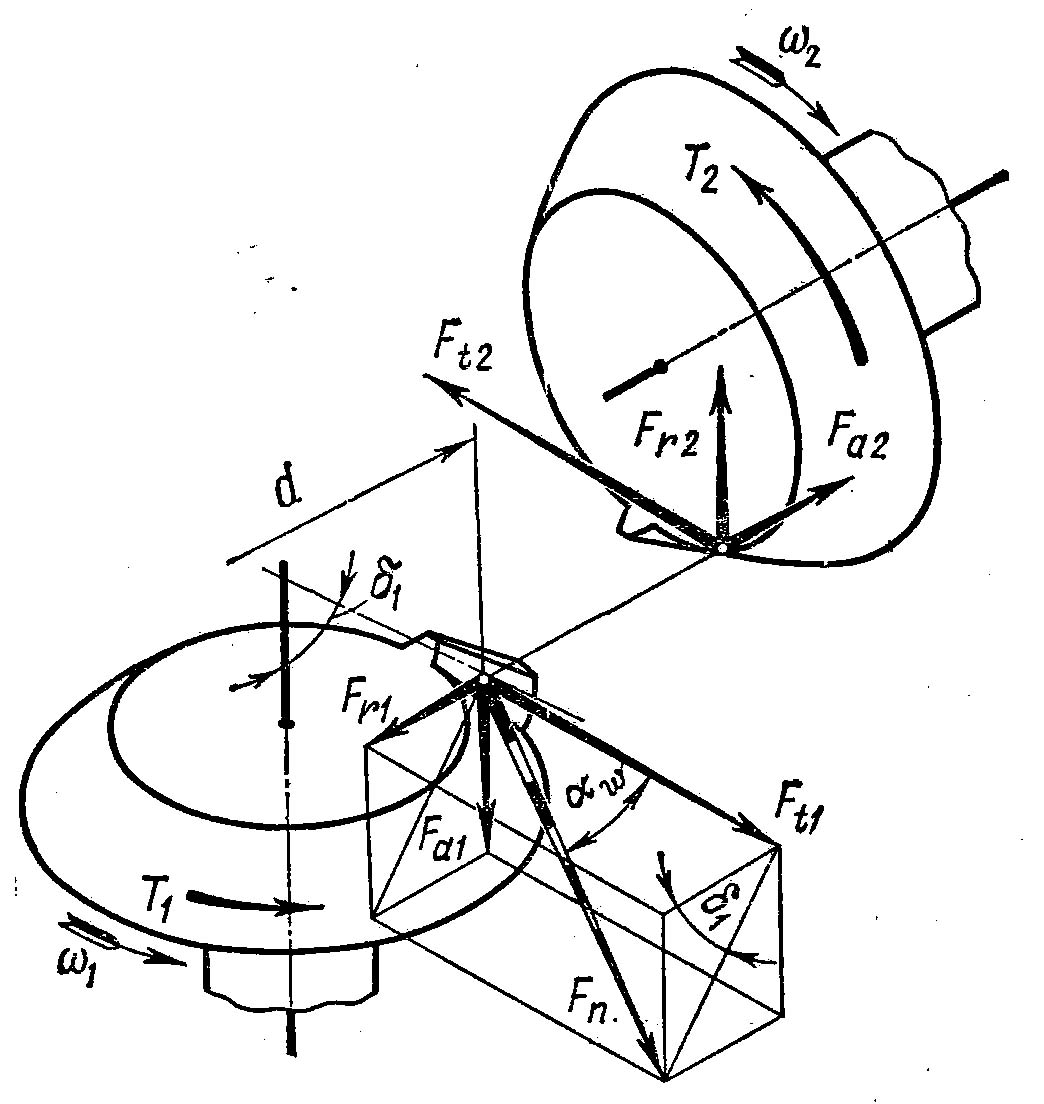
Рис. 3.24. Схема сил в конической прямозубой передаче.