
- •Подбор подшипников качения по статической грузоподъемности
- •Силовые соотношения в винтовой паре. Вывод формулы для определения момента трения в резьбе.
- •Виды повреждений зубчатых колес и меры их предупреждения
- •Общие требования, предъявляемые при проектировании деталей машин.
- •Вывод формулы проверочного расчета прямозубых цилиндрических передач на изгиб.
- •Подбор радиального шарикового подшипника по динамической грузоподъемности при наличии радиальной и осевой силы
- •Материалы, применяемые в машиностроении.
- •Расчет цилиндрических прямозубых передач на контактную прочность.
- •Геометрия и кинематика конических передач.
- •Геометрия зацепления колес.
- •Конструкция подшипников скольжения, требования к материалам и материалы вкладышей.
- •Подшипники качения, достоинства и недостатки. Разновидности и классификация.
- •Расчет косозубых цилиндрических передач на изгиб.
- •Определение допускаемых напряжений изгиба зубчатых колес.
- •Расчет валов на усталостную прочность
- •Резьбовые соединения. Виды резьб.
- •Материалы зубчатых колес и методы их термической и химико-термической обработки.
- •Основные сведения о зубчатых передачах. Геометрия и кинематика.
- •Эвольвента и эвольвентное зацепление. Геометрические соотношения в эвольвентном зубчатом зацеплении
Вывод формулы проверочного расчета прямозубых цилиндрических передач на изгиб.
Поломка зубьев связана с напряжениями изгиба, вследствие усталости материала от длительно действующих нагрузок. Расчет на изгиб сводится к проверке условия:
![]() (2.3.19)
(2.3.19)
При
выводе расчётной формулы для определения
напряжений изгиба принимают следующие
допущения:
1) вся нагрузка
![]() зацепления
передаются одной парой зубьев, которая
приложена к вершине зуба и направлена
по нормали к его профилю (сила трения
не учитываются); 2) зуб рассматривают
как консольную балку прямоугольного
сечения, что позволяет рассчитывать
его методами сопротивления материалов.
Фактически зуб представляет собой балку
с изменяющейся формой. Это учитывается
введением в расчётные формулы
теоретического коэффициента концентрации
напряжений Кт.
Распределённую по
ширине венца зуба нагрузку заменяют
сосредоточенной силой
,
которую переносят по линии действия на
ось зуба и раскладывают на две составляющие:
изгибающую зуб
зацепления
передаются одной парой зубьев, которая
приложена к вершине зуба и направлена
по нормали к его профилю (сила трения
не учитываются); 2) зуб рассматривают
как консольную балку прямоугольного
сечения, что позволяет рассчитывать
его методами сопротивления материалов.
Фактически зуб представляет собой балку
с изменяющейся формой. Это учитывается
введением в расчётные формулы
теоретического коэффициента концентрации
напряжений Кт.
Распределённую по
ширине венца зуба нагрузку заменяют
сосредоточенной силой
,
которую переносят по линии действия на
ось зуба и раскладывают на две составляющие:
изгибающую зуб
![]() и
сжимающую
и
сжимающую
![]() ,
где
,
где
![]() -
угол направления нормальной силы Fn. Он
несколько больше угла зацепления
-
угол направления нормальной силы Fn. Он
несколько больше угла зацепления
![]() .Напряжение
изгиба в опасном сечении (вблизи хорды
основной окружности), т.е. напряжение
на растянутой стороне зуба, где возникают
усталостные трещины рис.2.3.13.
.Напряжение
изгиба в опасном сечении (вблизи хорды
основной окружности), т.е. напряжение
на растянутой стороне зуба, где возникают
усталостные трещины рис.2.3.13.
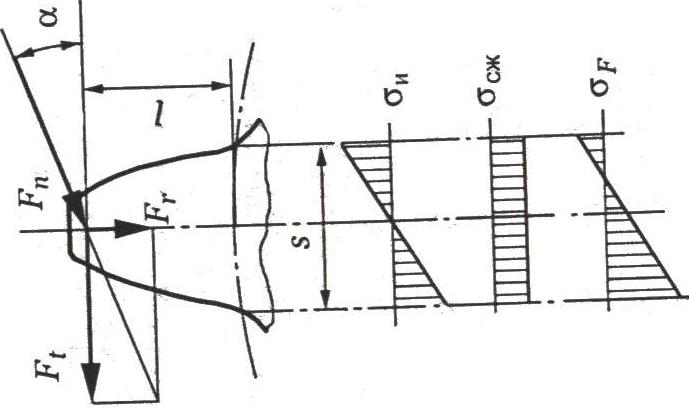
Рисунок 2.3.13 Эпюры распределения напряжений по ширине зуба
Напряжения определяются отношением внешней силы к моменту сопротивления сечения. Тогда после подстановки в исходную формулу, формула проверочного расчёта прямозубых передач:
![]() (2.3.20)
(2.3.20)
где
![]() и
и
![]() -
расчётное и допускаемое напряжения
изгиба, Н/мм2.
Ft – окружная сила,
H,
b и m – ширина и модуль зубчатого
колеса или шестерни, мм,
YF – коэффициент
формы зуба – величина безразмерная,
зависящая от числа зубьев z или zv и
коэффициента смещения х. Значения YF для
зубчатых колёс без смещения приводятся
в справочнике,
-
расчётное и допускаемое напряжения
изгиба, Н/мм2.
Ft – окружная сила,
H,
b и m – ширина и модуль зубчатого
колеса или шестерни, мм,
YF – коэффициент
формы зуба – величина безразмерная,
зависящая от числа зубьев z или zv и
коэффициента смещения х. Значения YF для
зубчатых колёс без смещения приводятся
в справочнике,
![]() -коэффициент
нагрузки при расчете на изгиб,
-коэффициент
нагрузки при расчете на изгиб,
![]() -
коэффициент нагрузки, учитывающий
распределение нагрузки между зубьями
(для прямозубых передач
-
коэффициент нагрузки, учитывающий
распределение нагрузки между зубьями
(для прямозубых передач
![]() ),
),
![]() -
коэффициент нагрузки, учитывающий
неравномерность распределения нагрузки
по ширине зубчатого венца (по длине
контактных линий),
-
коэффициент нагрузки, учитывающий
неравномерность распределения нагрузки
по ширине зубчатого венца (по длине
контактных линий),
![]() -
коэффициент нагрузки, учитывающий
дополнительные динамические нагрузки,
-
коэффициент нагрузки, учитывающий
дополнительные динамические нагрузки,
![]() -
допускаемое напряжение изгиба,
-
допускаемое напряжение изгиба,
![]() -
предел выносливости зубьев при изгибе,
-
предел выносливости зубьев при изгибе,
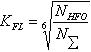 -
коэффициент долговечности при изгибе,
-
коэффициент долговечности при изгибе,
![]() -
базовое число циклов при изгибе,
-
базовое число циклов при изгибе,
![]() =
1,55- 1,75 - допускаемый коэффициент запаса
прочности,
Зубья шестерни и колеса
будут иметь примерно равную прочность
на изгиб при условии
=
1,55- 1,75 - допускаемый коэффициент запаса
прочности,
Зубья шестерни и колеса
будут иметь примерно равную прочность
на изгиб при условии
![]() (2.3.21)
(2.3.21)
Модуль
зубьев m определяют расчётом на изгиб,
исходя из межосевого расстояния
![]() ,
полученного из условия контактной
прочности. В этом случае для получения
расчётной формулы надо в выражении
(2.3.20):
,
полученного из условия контактной
прочности. В этом случае для получения
расчётной формулы надо в выражении
(2.3.20):
![]() заменить
ft на 2Т/d, где
заменить
ft на 2Т/d, где
![]() .
Тогда, решив уравнение
.
Тогда, решив уравнение
![]() относительно
модуля m, при некоторых средних значениях
коэффициентов
относительно
модуля m, при некоторых средних значениях
коэффициентов
![]() ,
и
получим
формулу для приближенного определения
модуля:
,
и
получим
формулу для приближенного определения
модуля:
(2.3.22)
В
эту формулу вместо
подставляют
меньшее из
![]() и
и
![]() .
Полученное значение модуля округляют
в большую сторону до стандартного.
Модуль колес рекомендуется принимать
минимальным. Уменьшение модуля и
соответствующее увеличение числа зубьев
способствует уменьшению удельного
скольжения, что увеличивает надежность
против заедания. При малом модуле
увеличивается коэффициент торцевого
перекрытия
.
Полученное значение модуля округляют
в большую сторону до стандартного.
Модуль колес рекомендуется принимать
минимальным. Уменьшение модуля и
соответствующее увеличение числа зубьев
способствует уменьшению удельного
скольжения, что увеличивает надежность
против заедания. При малом модуле
увеличивается коэффициент торцевого
перекрытия
![]() .
То есть увеличивается плавность работы
зацепления и к.п.д., уменьшается шум.
.
То есть увеличивается плавность работы
зацепления и к.п.д., уменьшается шум.
