Учреждение образования «Международный государственный экологический университет имени А.Д.Сахарова»

Факультет мониторинга окружающей среды

Тимощенко А.И., Хаджинов Е.М.

Физика. Квантовая физика. Математический аппарат квантовой механики

Учебно-вспомогательное пособие

для специальности 1-100 01 01 «Ядерная и радиационная безопасность»

Минск – 2011

Предисловие

Данное пособие предназначено для закрепления материала, изученного на лекциях и практических занятиях по теме 1 «Математический аппарат квантовой механики» дисциплины «Физика», раздел: «Квантовая физика». Материал данной темы представляет обычно значительную трудность для понимания, не в последнюю очередь потому, что необходимость применения изучаемого в разделе математического аппарата непосредственно не вытекает из опыта. Более того, экспериментальное описание явлений, к которым он применяется, во многом опирается на теоретические понятия и определения, возникающие в математическом аппарате. Эта ситуация необычна для начинающего изучать квантовую физику после классических разделов механики, молекулярной физики и термодинамики, электромагнетизма, оптики, где, как правило, применение математического аппарата обуславливается моделями, непосредственно связанными с наблюдениями и экспериментами.

Изложение материала в данном пособии построено в виде отдельных логически связанных между собой пунктов с целью акцентировать внимание читателя на отдельных определениях и свойствах, необходимых для запоминания и последующего усвоения. Данное пособие не является пособием по функциональному анализу и теории линейных операторов на линейных пространствах функций, в нем не преследуется цель дать математически безупречное определение абсолютно всех вводимых понятий, как, например, понятие гильбертова пространства, полноты системы собственных функций (векторов состояния) эрмитового оператора и т.п. Задача пособия – дать эвристическое введение в математический аппарат квантовой механики, обращая внимание там, где это необходимо, на некоторые детали, которые следует учитывать при его практическом применении. Для закрепления материала в тексте разделов и в конце их предлагается выполнить соответствующие упражнения, а также ответить на учебные вопросы.

Оглавление

1. Пространство волновых функций 4

2. Линейные операторы 6

3. Задача на собственные значения и собственные функции линейных операторов 15

4. Основы теории представлений. Дискретный спектр 20

5. Основы теории представлений. Непрерывный спектр 25

6. Среднее значение оператора. Соотношения между среднеквадратичными значениями некоммутирующих операторов 33

7. Оператор как функция от параметра 42

8. Функции от операторов 42

1. Пространство волновых функций

1. Объектом изучения в квантовой механике являются механические системы, положение которых в пространстве характеризуется обобщенными координатами qⁱ, i = 1,…,s, где s – число степеней свободы.

2. Будем рассматривать случаи, когда состояние квантовомеханической системы можно описать с помощью комплекснозначных функций обобщенных координат qⁱ: (q) = (q¹,…, q^s), являющихся элементами линейного пространства A над полем комплексных чисел . На эти функции накладываются требования дифференцируемости необходимое число раз и квадратичной интегрируемости. В квантовой механике эти функции называются волновыми функциями.

3. На пространстве волновых функций определяется скалярное произведение функций

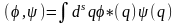,                                                   (1)

где d^sq = dq¹…dq^s – элемент координатного объема в конфигурационном пространстве механической системы. В частности скалярный квадрат функции

,

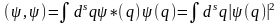что объясняет необходимость наложения на волновые функции условия квадратичной интегрируемости.

Из (1) вытекает следующее свойство скалярного произведения

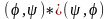.                                                           (1)

4. С помощью скалярного произведения (1) вводится понятие нормы вектора (q), или его длины:

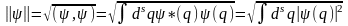,                              (2)

так как интеграл 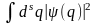положителен везде в области определения функции (q) и обращается в ноль только при (q) = 0.

Легко видеть, что (2) действительно обладает всеми свойствами нормы:

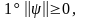 причем 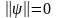тогда и только тогда, когда  = 0;

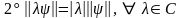;                                                                                             (3)

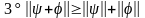(неравенство треугольника).

5. Пространство A может быть конечномерным или бесконечномерным. В последнем случае число измерений может быть как счетно, так и несчетно. Такое пространство со скалярным произведением (1) называется гильбертовым пространством.

6. Наряду с пространством A волновых функций (q), заданных в некоторой области конфигурационного пространства механической системы можно рассматривать пространство A_cket абстрактных векторов 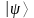над полем комплексных чисел , такое, что свертка его с вектором 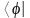из сопряженного абстрактного пространства A_bra будет давать скалярное произведение (1)

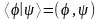.                                                           (4)

Векторы называются кэт-векторами, а векторы – бра-векторами соответствующего состояния, описываемого волновой функцией, стоящей в скобках. Названия происходят от разбиения на слоги слова «bra-cket» – «скобка» (Дирак). С абстрактными векторами и можно работать также как с самими волновыми функциями, рассматриваемыми как векторы: умножать на числа и складывать. При этом будут получаться другие векторы из пространств A_cket и A_bra соответственно. Только теперь векторы и нельзя рассматривать как некоторые комплекснозначные функции обобщенных координат. Но они так же, как и сами функции (q) и (q) будут рассматриваться как метки некоторого состояния квантовой системы.

Число 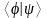можно представлять себе как результат скалярного произведения бра-вектора на кэт-вектор : .

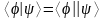7. Волновая функция (q) может представлять собой набор волновых функций col(¹(q),…, ^N(q)) – координат некоторого вектора в N-мерном линейном пространстве, каждая из которых является, в свою очередь, элементом линейного пространства A. В этом случае скалярное произведение (1) определяется как

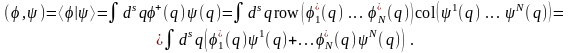  (5)

Знак ⁺ используется для обозначения т.н. эрмитовского сопряжения, которое в случае конечномерных пространств представляет собой сочетание двух действий: комплексного сопряжения и транспонирования (превращение столбцов в строки и наоборот). Смысл абстрактных векторов и при этом, в принципе, не меняется. Можно рассматривать многокомпонентные вектор-строки

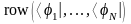
и вектор-столбцы

,

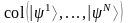перемножая их слева направо по правилу «строка на столбец». Однако, все это уже, в принципе, заложено в символах и . В дальнейшем будем говорить, что операция эрмитовского сопряжения ⁺ переводит кэт-векторы в бра-векторы и наоборот, понимая ее в этом случае абстрактно в такой же мере, в какой мере абстрактными являются сами векторы :

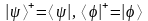.                                                     (6)

Тогда, например, свойство (1) может быть получено путем естественного применения операции эрмитового сопряжения ⁺, понимаемой как сочетание операции комплексного сопряжения и транспонирования в смысле, определенном в (6).

Учебные вопросы

1. Сформулируйте определение скалярного произведения волновых функций.

2. Дайте определение нормы волновой функции.

3. Как вводятся в рассмотрение абстрактные векторы состояния Дирака (кэт- и бра-векторы)?

4. Как обобщается понятие скалярного произведения на случай многокомпонентных собственных функций?