15. Вязкотекучее состояние вмс

Вязкотекучее состояние полимеров: это состояние полимеров относится к их расплавам, для него характерны преимущественно необратимые деформации, т.е течение. Перемещение, т.е рептация макромолекул при течении, осуществляется путём направленной диффузии сегментов. При этом необходимо выполнение двух условий- наличие «тепловой» энергии, достаточной для преодоления межмолекулярного взаимодействия, и микропустот – «дырок», куда осуществляется перемещение сегмента. Последнее условие является определяющим в области температур, близких к температуре стеклования: Т_с Т ( Т_с+120⁰С). В этой области существует непосредственная связь между сдвиговой вязкостью и свободным объёмом. Она выражается эмпирическим уравнением, Дулиттом: = lnA+ , где А и В – эмпирические константы, последняя из которых близка к единице; V Vcb- удельный и свободный объёмы на 1 г соответственно. При T (Tc+120⁰C) скорость перемещения сегментов в основном определяется энергетическим фактором. В этих условиях зависимость вязкости полимера от температуры описывается формулой Френкеля – Эйринга, выведенной на основе активациооной теории ~ exp

Одним из проявлений вязкоупругих свойств расплавов являются так называемые нормальные напряжения, возникающие при приложении к расплаву сдвигового напряжения и направленные перпендикулярно к нему. Это явление получило название эффекта Вайссенберга, такой эффект наблюдается при расплаве полимера, заключённого между цилиндрами – вращающимся и неподвижным. При вращении вала( внутреннего цилиндра) возникает сдвиговое усилие, направленное по касательной к жидкости. Макромолекулярные клубки вследствие этого деформируются, однако, тепловое движение сегментов стремится вернуть их к первоначальной конформации гауссова клубка. В результате возникает напряжение, направленное перпендикулярно к сдвиговому, заставляющее « ползти» жидкость вверх по валу.

16. Радикальная сополимеризация. Уравнение состава сополимера. Схема Алфея-Прайса (q-e).

Радикальная сополимеризация

Полимеры, получаемые при совместной полимеризации (сополимеризации) двух или большего количества мономеров, называются совместными полимерами или сополимерами. Макромолекулы сополимеров содержат остатки всех присутствующих в исходной реакционной смеси мономеров.. Рассмотрим бинарную сополимеризацию . При реакции мономеров М₁ и М₂ со свободными радикалами R, возникшими при распаде инициатора, образуются новые радикалы, один из которых имеет концевое звено М_1, а второй — концевое звено М₂:

К аждый из образовавшихся таким образом радикалов может реагировать как с мономером М₁, так и с мономером М₂, причем вероятность той или иной из этих элементарных реакций опреде­ляется ее константой скорости. Допуская, что реакционная способность растущих радикалов зависит только от активности концевого звена, но не от числа и строения ранее присоединившихся мономеров, можно различить четыре типа элементарных реакций и соответст­вующие им константы скорости —k1.1, k1.2, k1.3, k1.4: Элементарная реакция Скорость

1)М1^. + М1 М1^. K1.1 [М1^. ][M₁] гоморост

2)М1^. + М2 М2^. K1.2 [М1^. ][M₂] перекрестный рост

3)М2^. + М2 М2^. K1.3 [М2^. ][M₂] гоморост

4)М2^. + М1 М1^. K1.4 [М2^. ][M₁] перекрестный рост

На основании этой схемы можно вывести ур-ние, связывающее составы сополимера и мономерной смеси:

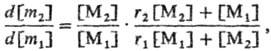
где [M1] и [М2]- текущие концентрации мономеров, [m1] и [m2]-текущие концентрации мономерных звеньев в сополимере. Параметры r1 и r2 наз. константами сополимеризации или относит. активностями мономеров. От этих величин зависит вид кривой «мономерный состав — полимерный состав». Когда активность мономера М₂ выше активности мономера М_1; образующийся сополимер богаче мономером М₂, чем мономерная смесь при любом исходном соотно­шении мономеров. Если, наоборот, М₁ активнее, тогда сополимер всегда содержит больше M₁ по сравнению с мономерной смесью.

Строение сополимера характеризуется количеством отрезков моле­кулярной цепи, состоящих из одних остатков М₁ или М₂, и числом этих остатков в каждом отрезке.

О характере чередования мономерных остатков можно также су­дить по блоковому числу, представляющему собой среднее число бло­ков, приходящееся на 100 звеньев. Например, для сополимера

M₁—М₂—М₁— M₁—М₂—М₂—М₂—М₁—М₂—М₂,

содержащего 10 звеньев и 6 блоков, оно равно 60. Блоковое число вычисляется по составу сополимера и значениям г_х и г₂, найденным из эксперимента. Существует влияние температуры и давления на радикальную сополимеризацию, это может быть установлено из уравнения Аррениуса.

Состав статистического сополимера не зависит от общей скорости процесса сополимеризации и от природы инициатора.

Уравнение состава сополимера

Для оценки среднего состава сополимера при различных степенях превращения при известных значениях r1 и r2 или же для вычисления r1 и r2 по известному составу исходной смеси мономеров и состава сополимера пользуются интегральным уравнением Майо-Льюиса.

где [А₀], [В₀] и [А], [В] - соответственно начальные и конечные концентрации мономеров. На практике при малых степенях превращения удобно пользоваться упрощенными уравнениями:

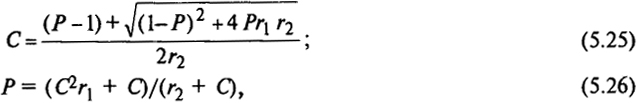
где С и Р - мольное соотношение мономеров в исходной смеси и в сополимере соответственно. Зная r1 и r2, можно рассчитать примерный состав исходной смеси мономеров для получения сополимера определенного состава.

Схема Алфея-Прайса (Q-e)

каждая константа роста цепи выражается четырьмя параметрами:

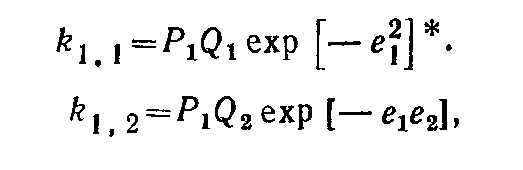
где Р — величина, отражающая реакционную способность растущего радикала; Q — параметр, пропорциональный степени сопряженности двойной связи с заместителями **. Избыточные заряды радикала М₁^. и мономера М₂, обусловленные поляризу­ющим влиянием тех же заместителей, обозначаются соответственно е₁ и е₂, они могут иметь знак + или - . При этом делается маловероятное допущение о равенстве показателя е у мономерной молекулы и радикала, имеющего на конце такую же мономерную группу. Подстав­ляя значения k _1.1, k _1.2 в выражение для r1, получаем

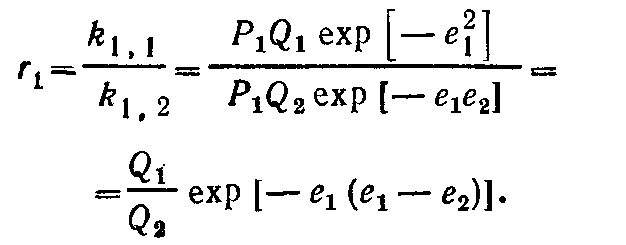
Аналогично

Попытки обосновать схему Q — е теоретически не увенчались успехом, поэтому лучше считать ее эмпирической. Тем не менее справедливость конечных выводов этой схемы подтверждается экспериментально. схема Q — е в случае сополимеризаций трех различных мономеров - термополимеризации.