6) Структура полимерной цепи. Регулярные и нерегулярные полимеры. Уровни конфигурации макромолекулы.

Структура – закономерная пространственная, устойчивая организация взаимодействующих частиц вещества. Структура полимера характеризуется строением макромолекул и способом их взаимной упаковки. Структура макромолекулы определяется конфигурацией, конформацией и гибкостью цепи.

На уровне дальнего конфигурационного порядка различают регулярные и нерегулярные макромолекулы.

Регулярная макромолекула – макромолекула, структура которой в основном включает повторение идентичных составных звеньев, соединенных друг с другом вдоль цепи одинаковым образом.

Нерегулярная макромолекула – макромолекула, структура которой в основном включает составные звенья, соединенные друг с другом вдоль цепи неодинаковым образом.

Конфигурационные уровни макромолекулы :

1. конфигурация мономерного звена (R, S)

2. ближний конфигурационный порядок (изотактическая или синдиотактическая диада)

3. дальний конфигурационный порядок (изотактическая или синдиотактическая , или атактическая макромолекула)

4. конфигурация цепи в целом (линейная или нелинейная)

7. Уровни иерархии конформации макромолекулы.

Конформация макромолекулы – взаимное расположение атомов в макромолекуле, изменяющееся в процессе теплового движения или под действием внешних сил.

Конформация цепи определяется длинами связей, углами между связями (валентными углами) и углами внутреннего вращения.

Конформационные уровни макромолекулы:

1. Конформация мономерного звена;

2. Ближний конфармационный порядок – конформация диады;

3. Дальний конфармационный порядок – конформация последовательности из n звеньев;

Конформационное повторяющееся звено в кристаллическом ВМС – наименьшее звено в данной конформации, которое повторяется с помощью операций симметрии, включающих в себя трансляцию.

4. Конформация цепи в целом.

Конформация мономерного звена

Синперипланарная конформация, обозначается буквой латинского алфавита С, называется также цис-конформацией или заслоненной коформацией. Угол внутреннего вращения φ=0.

Антиперипланарная конформация, обозначается буквой Т, называется также транс-конформацией или заторможенной конформацией. Углы внутреннего вращения = 180.

Синклинальная конформация, обозначается буквой G, называется также гош-конформацией или скошенной конформацией. Углы внутреннего вращения = 60.

При вращении атомных групп вокруг связей основной цепи по часовой стрелке конформации обозначают знаком «+», например (G+), против часовой стрелки – знаком «-», например (G-).

На примере молекулы 1,2-дихлорэтана. В синперипланарной конформации расстояние между атомами хлора минимальное, а в антиперипланарной – максимальное. В синклинальных конформациях между атомами хлора реализуются промежуточные расстояния. Расстояние между атомами определяет энергию их взаимодействия. Следовательно, синперипланарная конформация соответствует максимуму потенциальной энергии молекулы из за отталкивания атомов хлора и, значит, неустойчива. Энергетическому минимуму отвечает устойчивая антиперипланарная конформация, при которой один атом хлора повернут вокруг С-С связи на угол = 180 относительно другого. Синклинальные конформации менее устойчивы, чем антиперипланарная, но более устойчивы по сравнению с синперипланарной.

Конформация диады

Конформация виниловой диады, подобно конформации молекулы 1,2-дихлорэтана, определяется равновесием антиперипланарного (Т) и двух синклинальных (G ) изомеров.

Дальний конформационный порядок

Дальний конформационный порядок виниловых макромолекул определяется чередованием антиперипланарного и двух синклинальных изомеров. Чередование может быть беспорядочным и закономерным. Беспорядочное чередование характерно для цепей аморфных виниловых ВМС, закономерное – для кристаллических.

Конформация цепи в целом

Конформация цепи в целом – усредненная по времени и пространству форма, которую макромолекула принимает в результате внутреннего теплового движения и внешних воздействий.

Линейные цепи существуют в следующих конформациях: клубок; глобула; складчатая; стержень.

Клубок. Является конформацией гибких макромолекул, обладающих выраженной способностью к конформационным переходам.

Статистический клубок – совокупность мгновенных свернутых конформаций.

Характерныйе особенности статистического клубка: низкая плотность звеньев; флуктуация плотности звеньев в объеме клубка.

Глобула. Образуется в результате предельного скручивания макромолекулы в компактную сферическую частицу. Среднеквадратичное расстояние между концами цепи в конформации глобула близко к нулю.

Статистическая глобула – совокупность мгновенных предельно свернутых конформаций.

Характерные особенности статистической глобулы: высокая плотность звеньев; отсутствие больших флуктуаций плотности звеньев в объеме глобулы.

Условия реализации глобулярной конформации: преобладание внутримолекулярного взаимодействия над межмолекулярным; низкое т/д сродство высокомолекулярного соединения и р-ля.

Складчатая конформация. Это конформация гибких макромолекул. Возникает в результате поворота фрагментов цепи на 180 и складывания цепи «на себя», например спирали изотактического полипропилена.

Условие реализации: самопроизвольная кристаллизация гибкоцепных ВМС.

Стержень. Среднеквадратичное расстояние между концами цепи в конформации стержень равно контурной длине цепи. Стержень представляет собой предельно упорядоченную конформацию.

Условия реализации: жесткость цепи – самопроизвольно конформацию стержень принимают жесткие цепи в ра-ре, расплаве, в кристалле; принудительное внешнее воздействие – обуславливает конформацию стержень для гибких цепей.

Кристаллическое фазовое состояние ВМС может быть организовано макромолекулами в складчатой, вытянутой или глобулярной конформации; жидкокристаллическое – цепями в вытянутой конформации; аморфное – цепями в конформациях клубок, глобула, стержень.

Конформационные уровни макромолекулы изотактического полипропилена:

1. Конформация мономерного звена – равновесие изомеров Т и G±;

2. Ближний конформационный порядок – равновесие изомеров Т и G±;

3. Дальний порядок – спираль класса 3₁ (n=3), в которой реализуется последовательность …….ТGТGТGТG…….;

4. Конформация цепи в целом – складчатая.

8.Термодинамическая и кинетическая гибкость макромолекулы. Количественные характеристики гибкости макромолекулы: среднеквадратичное расстояние между концами цепи, радиус инерции макромолекулы, длина сегмента макромолекулы.

Т/д гибкость макромолекулы – способность макромолекулы к конформационным переходам под влиянием внутреннего теплового движения. Она реализуется в очень разбавленных растворах, в которых цепи находятся в изолированном состоянии, при отсутствии каких-либо внешних воздействий. Т/д гибкость связана с размерами макромолекулы рассчитываемыми для цепи со свободным вращением. Количественной мерой т/д гибкости цепи является параметр σ

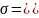
Чем больше σ, тем меньше т/д гибкость цепи

Наиболее универсальной мерой оценки гибкости цепи является величина сегмента Куна А.. Сегмент является некоторым фиктивным образованием, принятым в модели.

Среднеквадратичное расстояние между концами цепи:

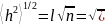
l – длина мономерного звена; L- контурная длина цепи; n – степень полимеризации.

Среднеквадратичный радиус инерции цепи – среднеквадратичное расстояние от центра массы макромолекулярного клубка до каждого из звеньев цепи.

Кинетическая гибкость – скорость конформационных переходов макромолекулы под действием внешнего поля. Она зависит от величины потенциального барьера, молекулярной массы и степени сетчатости полимера и температуры.

Кинетическая гибкость цепи оценивается величиной кинетического сегмента, т.е. наименьшего отрезка цепи, который уже проявляет кинетическую гибкость. С кинетической гибкостью связаны температуры стеклования полимеров. Полимеры, цепи которых имеют высокую кинетическую гибкость, характеризуются низкими температурами стеклования.

9. Модель свободно-сочлененной цепи: вывод и анализ уравнения, связывающего среднеквадратичное расстояние между концами цепи с контурной длиной цепи. Модель с фиксированными валентными углами. Модель заторможенного вращения.

Модель свободносочлененной цепи

Основные допущения: цепь состоит из множества мономерных звеньев; валентные углы в цепи не фиксированы; мономерные звенья не взаимодействуют; звенья соединены шарнирно, и вращение звеньев друг относительно друга абсолютно свободно.

Свободносочлененная цепь непрерывно изменяет конформацию, и поэтому конформацию описывают посредством статистических характеристик. Основная статистическая геометрическая характеристики гибкости – среднее расстояние между концами цепи.

Среднеквадратичное расстояние между концами свободносочлененной цепи:

l – длина мономерного звена; L – контурная длина цепи; n – степень поимеризации.

Модель с фиксированными валентными углами

Основные положения: Цепь состоит из множества мономерных звеньев; Валентные углы в цепи фиксированы; Вращение звеньев друг относительно друга ограничено фиксацией валентных углов.

Среднеквадратичное расстояние между концами цепи с фиксированными валентными углами:

- угол, дополнительный к валентному.

Модель заторможенного вращения

Основные положения: Цепь состоит из множества мономерных звеньев; Валентные углы в цепи фиксированы; Вращение звеньев друг относительно друга ограничено фиксацией валентных углов и энергетическим взаимодействием мономерных звеньев.

В этой модели в соответствии с ее положениями вводится новое ограничение: из доступного для вращения звеньев пространственного объема исключается неустойчивая синперипланарная конформация.

Расчеты на основе модели заторможенного вращения дают следующее выражение для среднеквадратичного расстояния между концами цепи, известное как формула Тейлора:

- средний косинус угла заторможенного внутреннего вращения.