40) Вязкость растворов полимеров. Определение молекулярной массы и среднеквадратичного расстояния между концами цепи методом вискозиметрии.

Вязкость (внутреннее трение жидкости) обусловлена взаимодействием молекул жидкости и проявляется при ее течении. Течение жидкости в капилляре диаметром x характеризуется градиентом скорости dυ/dx вследствие того, что молекулярный слой, непосредственно примыкающий к стенке капилляра, остается неподвижным, а слой, находящийся в центре капилляра, движется с максимальной скоростью. Ламинарное течение жидкости описывается законом Ньютона, согласно которому напряжение сдвига τ, вызывающее течение жидкости, пропорционально градиенту скорости течения:

τ=η*( dυ/dx) Коэффициент пропорциональности η называется коэффициентом вязкости или просто вязкостью.

Вязкость можно рассматривать как меру энергии, рассеиваемой в форме теплоты в процессе течения жидкости. Растворы полимеров обладают более высокой вязкостью по сравнению с низкомолекулярными жидкостями.

Измерение вязкости жидкостей проводят чаще всего в капиллярных вискозиметрах. Оно основано на использовании уравнения Пуазейля Q= (III.15)

где Q – количество жидкости, протекающей через капилляр за время t; r, l – радиус и длина капилляра соответственно; ∆Р – разность давлений на концах капилляра.

Если жидкость течет под действием собственного веса, то ∆Р=∆h*ρ*g (здесь ∆h – высота столба жидкости в приборе; ρ – плотность жидкости; g – ускорение свободного падения): η=К*ρ*t, где К=(πr⁴∆hg)/8Ql называется постоянной вискозиметра

При исследовании разбавленных растворов полимеров определяют обычно вязкость относительную при условии, что плотности разбавленного раствора и чистого растворителя практически совпадают, равно η_отн=η/η₀=t/t₀, где t и t₀ – времена истечения соответственно раствора и чистого растворителя. Отношение (η – η₀)/η₀ показывает относительный прирост вязкости вследствие введения в растворитель полимера и называется удельной вязкостью η_уд, отношение η_уд/С – приведенной вязкостью η_пр и limη_уд/С при С→0 называется характеристической вязкостью [η].

Вязкость разбавленного раствора непроницаемых сплошных невзаимодействующих сферических частиц описывается формулой Эйнштейна: η/η₀=1+ 2,5φ

где φ – объемная доля растворенного вещества; 2,5 – коэффициент, учитывающий гидродинамическое взаимодействие жесткой сферической частицы со средой.

Уравнение Энштейна означает, что характеристическая вязкость раствора сплошных невзаимодействующих частиц (не обязательно сферических, тогда коэффициент 2,5 будет другим) определяется только плотностью вещества и не зависит от молекулярной массы и размеров частиц. Это происходит вследствие того, что масса таких частиц строго пропорциональна их объему.

Допустим для простоты, что макромолекулярный клубок в θ-растворителе имеет форму шара радиуса R_е (радиус эквивалентной сферы), который примем равным R¯_g (среднему радиусу инерции). Считая эти частицы непроницаемыми для растворителя в потоке, можно применить к ним уравнение Энштейна, причем объемная доля вещества в этом случае учитывает не собственный объем макромолекул, а их эффективный объем в растворе вместе с включенным в них растворителем. Тогда, учитывая, что в θ-условиях R¯_g²=ћ²_θ/6, преобразуем уравнение (III.16) к виду

[η]=2,5 π(ћ²_θ/6)^3/2 =Ф*((ћ²_θ)^3/2 /М) (III.17)

Это формула Флори-Фокса для вязкости полимера в θ-растворителе. Здесь Ф – постоянная Флори, в первом приближении не зависящая от свойств полимера.

В условиях, отличных от θ-условий, например в хороших растворителях, молекулярный клубок дополнительно набухает. Принимая, что формула Флори-Фокса справедлива также для раствора «полимер в хорошем растворителе» и подставляя значение (h²)^1/2 из выражения (III.11) в уравнение (III.17), получим:

[η]=Ф Сопоставляя это уравнение с уравнением (III.17) и пренебрегая зависимостью Ф от качества растворителя (что, вообще говоря, не вполне справедливо), можно оценить коэффициент набухания макромолекулы:

α= (III.18)

Большинство полимеров в растворах ведут себя отлично от эйнштейновских частиц, и для них наблюдается зависимость характеристической вязкости от молекулярной массы полимера. Эта зависимость обусловлена тем, что либо эффективный объем макромолекулярного клубка в растворе растет быстрее, чем его молекулярная масса, либо тем, что клубок имеет несферическую форму и частично проницаем для потока растворителя.

Выражая (ћ²)_θ^1/2 через молекулярную массу полимера: (ћ²)_θ=zb²=Mb²/M_c (где М_с – молекулярная масса сегмента) и подставляя это значение в уравнение (III.17), получим:

[η]_θ=Ф =K_θM^1/2

Это уравнение связывает характеристическую вязкость с молекулярной массой полимера в θ-условиях.

Для раствора полимера в любом растворителе имеем:

[η]=Ф (III.19)- уравнения Марка-Куна-Хаувинка.

Постоянная К=10^-2÷10^-5 зависит от температуры и природы полимера и растворителя. а изменяется в пределах: 0≤а≤2,0.

Зависимость приведенной вязкости от концентрации раствора полимера (рис. III.9) описывается уравнением Хаггинса:

η_уд/С=[η]+К'[η]²С (III.21)

где К' – константа Хаггинса, характеризующая взаимодействие макромолекул в данном растворителе.

В хороших растворителях К'=0,2-0,3, в плохих - К'≥0,5.

Характеристическая вязкость определяет поведение изолированных макромолекул. Она представляет собой меру потерь энергии на трение изолированных макромолекул о растворитель при их вращении в результате поступательного движения в потоке с градиентом скорости, отличным от нуля. Характеристическая вязкость зависит от размеров макромолекул в растворе, от природы растворителя и температуры раствора. В хорошем растворителе макромолекулярный клубок набухает и вязкость увеличивается.

Раствор можно считать разбавленным, если для него С<<1/[η]. Последнее неравенство означает, что объем раствора, занятый макромолекулами, значительно меньше общего объема раствора. Раствор считают умеренно концентрированным при условии С≈1/[η] и концентрированным – при С>>1/[η].

Константы К и а не зависят от молекулярной массы, для вязкости раствора полидисперсного полимера можно написать:

η_уд= =КМ¯_η^а откуда М¯_η=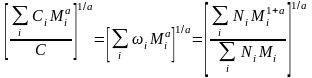

Сопоставляя это уравнение с уравнением (III.13), можно заключить, что М¯_η= М¯_ω только в частном случае при а=1.

Характеристические вязкости и молекулярные массы для одного и того же полимера, измеренные в двух разных растворителях, для которых константы а уравнения Марка-Куна-Хаувинка различны (например, в хорошем и плохом растворителях), различаются:

М¯_η1= ; М¯_η2=

Это обусловлено тем, что в хорошем растворителе макромолекулярные клубки находятся в относительно набухшем состоянии и средняя молекулярная масса более чувствительна к присутствию высокомолекулярной фракции, тогда как в плохом растворителе макромолекулы имеют более компактные конформации и вклады макромолекул разной длины различаются в меньшей степени. Отношение М¯_η1/ М¯_η2 может служить мерой полидисперсности, как и отношение М¯_ω/ М¯_n. Чем больше разность между а₁ и а₂, тем чувствительнее эта характеристика.