38. Термодинамические понятия, используемые в теории растворов полимеров.

Растворы нужно делать ТД устойчивыми. Важна природа растворителя.

Функция Гиббса (равновесность системы). Р,Т = const. ΔG=ΔH-TΔS, если система однокомпонентная. ΔG<0, то процесс самопроизвольный. Раствор не расслоится и будет существовать долго. ΔG>0,то раствор прекратит существование. Он расслоится. ΔH и ΔS влияют на концентрацию раствора.

Изменения энтропии смешенного идеального р-ра: ΔSсмеш.ид= -К(N₁lnx₁+N₂lnx₂), где х1,х2- мольные доли компонента, N_1,N₂-число молекул компонента, К- постоянная Больцмана.

Х	о	О	о
О	О	Х	Х
х	О	х	О

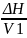Полимерная модель(звенья связаны ковалентными связями). Гильдебранд ввёл параметр растворимости- экспериментально измеренная величина для любого полимера, которая определяется энергией взаимодействия между молекулами в данном веществе. , где 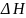- плотность энергии когезии (взаимодействия между веществами внутри системы), 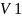- удельный объём данного компонента.

δ=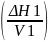 ^1/2-параметр растворимости Гельдебранда. Условие ΔЕ=Vφ₁φ₂*[( )^1/2-(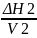 )^1/2]² или ΔЕ=Vφ₁φ₂ (δ₁-δ₂)². Параметр растворимости: бери растворитель, значение которого ближе к значению Гильдебрана полимера.

Основные уравнения ТД:

ΔGсмеси= Gр-ра – Gкомпонентов

ΔGсмеси= G р-ра – (Gрас-ль – Gраств. в-во).

ΔGсмеси= ΔН – ТΔSсмеси

1). ΔНсмеш<0, ΔSсмеш>0, то растворение экзотермическое, ΔS увеличивается. Энергия взаимодействия разнородных молекул больше, чем между однородными.

2). ΔНсмеш<0, ΔSсмеш<0, ΔНсмеш>ТΔS, то растворение экзотермическое. Сопровождается уменьшением энтропии. Она уменьшается за счёт захватывания растворителя. Такие системы расслаиваются при высоких Т. Они обладают низшей критической Тсмеш.

3). ΔНсмеш>0, ΔSсмеш>0, ΔНсмеш<ТΔS, то растворение эндотермическое. Расслаивание происходит при пониженных Т.

4). ΔНсмеш=0, ΔS<0, то атермическое растворение. Наблюдается при растворении полимера в гидрированном или собственном раст-ле.

В ТД рас-ов обычно пользуются парциальными величинами (хар-ют изменение экспериментальных (зависящих от массы) при добавлении бесконечно малого количества одного из компонентов).

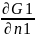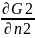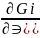Ğ₁=( )_P,T- химический потенциал (μ_i); Ğ₂=( )_P,T; Ğ_i=( )_P,T= μ_i

Для двухкомпонентной системы G=ΣG_in_i; G=G₁n₁+ G₂n₂; n_1>>n₂-разб.рас-р.

d μ_i=RT(dlnx_i)-изменение химического потенциала.xi- мольная доля i-ого ком-та в рас-ре. μ_i= μ_i⁰+ RTlnx_i; при введении другого компонента Δμ_i=μ_i- μ⁰= RTlnx_i.

39. Особенности термодинамики полимерных растворов. Энергетика растворения полимеров. Набухание полимеров. Фазовые диаграммы систем полимер-растворитель.

Фракционирование полимеров.

Уравнение связывающее ТД функцию молекулярными характеристиками раствора в равновесном состоянии π=f(М1, М2….). Модель Флори и Хагинса-решёточная модель регулярного р-ра (квазикристаллическая модель). Модель представляет объём р-ра как совокупность ячеек одинакового размера (двумерная решётка). Все макромолекулы считаются гибкими. Каждую ячейку решётки может занимать либо молекула растворителя, либо сегмент цепи. Они могут обмениваться местами между собой. n₁-число молекул растворителя,n₂-число цепей,S-число сегментов в цепи. Общее число ячеек n₁+ S* n₂.

Объёмная доля р-ля:φ1= 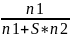;φ2= . Координационное числоυ – число контактов одной структурной единицы с окружающими. Необходимо рассчитать ΔG,ΔH,ΔS. КомбинаториальнаяS смешения ΔSк.

S=KlnW;ΔSк= -R(n₁lnφ₁+n₂lnφ₂)- комб. S растворения ВМС

Для НМС ΔSк= -K(n₁lnN₁+n₂lnN₂). При одинаковых мольных долях ВМС и НМС ΔSк ВМС намного больше ( ввиду большего объёма макромолекулы).

При переходе макромолекулы в раствор реализуется броуновское движение сегментов, которое неосущ. в ТВ агрегатном состоянии- физ. смысл большой ΔSк для ВМС. Аномально высокие значения ΔS смешения обуславливают отклонения р-ров ВМС от законов Рауля и Вант- Гоффа.

Определение величины ТД сегмента. Определяют Р(давление) пара рас-ля над рас-ом и Р пара чистого растворителя. Закон Рауля =N₁^*- эффективная мольная доля для полимеров рас-ля. Мольная доля рас-ля в рас-ре N₁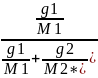^*= - кажущаяся Mr полимера- величина, эквивалентная Mr полимер гомолога, который образовался бы с данным растворителем.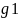 - масса навески.

Идеальный раствор. Расчёт энтальпии смешения ΔН= КTχn1φ2, где χ-число молекул растворителя, φ2-объёмная доля полимера.

Параметр Флори-Хагинса(константа Хагинса, коэффициент взаимодействия ) χ=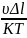 , где 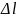- алгебраическая сумма энергий различных контактов. Константа характеризует энергию взаимодействия одной молекулы рас-ля, отнесенную к тепловой энергии.

Δе= , где е11,е22,е12- энергии одного контакта между одинаковыми и разными частицами соответственно.

Изменение свободной энергии смешения

ΔG=ΔH-TΔS

ΔG=KTχn₁φ₂+ KT(n₁lnφ₁+n₂lnφ₂)=KT(χn₁lnφ₂+ n₁lnφ₁+ n₂lnφ₂), где χn₁lnφ₂- энергетический терм, n₁lnφ₁+ n₂lnφ₂- комбинаториальный терм.

ΔG→π (осмотическое Р) . Показатель ТД сродства между полимером и растворителем отнесённый к еденице объёма π=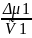 , где Ṽ=парциальный мольный объём рас-ля. Чем меньше π, тем меньше 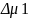=> тем выше ТД сродство растворителя к полимеру.

Уравнение состояния полимера в р-ре (разбавл. р-р)

Приведенное осмотическое давлени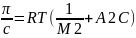е , где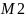 -Mr ВМС. Второй вириальный коэфициент А2= .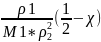

Зависимость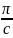 от С. =RT(A1+A2C+A3C²+……), A1=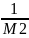 . При масых С зависимость считают линейной (берут первые 2 члена). Определяется средняя Mr. Mrембранная осмометрия позволяет определить Mr в диапазоне 3*10⁴-1*10⁶. Другой метод концевых групп.

В ТД хорошем растворителе α большое, в плохом α невелико.

В определённых растворителях при определённой Т межсегментальные, когезионные силы уравновешиваются дисперсионными силами взаимодействия между сегментами и частицами растворителя. В результате размеры клубка остаются невозмущёнными. α=1→(ĥ²)^1/2=(ĥ₀²)^1/2. θ- растворитель занимает промежуточное положение между плохим рас-ем и осадителем. Т при которой α=1назыв. θ-температурой (или Т Флори). Идеальный растворитель бывает только при θ- температуре (это Т, при которой разбавленные р-ры ВМС подчиняются идеальным законам Рауля и Вант- Гоффа). При θ-температуре определяется Mr сегмента по закону Вант- Гоффа. В θ-усл. А2=0, Т_θ=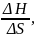 ΔG=0.

Набухание внутри кристалла.

Набухание – это процесс поглощения или сорбции низкомолекулярных жидкостей (или их паров) полимером. Набухание сопровождается увеличением массы, объёма и изменением структуры полимера. Скорость проникновения растворителя от поверхности в глубь полимера зависит от степени термодинамического сродства растворителя и полимера, уровня межмолекулярного взаимодействия в полимере, температуры и других условий процесса. На начальной стадии набухания распределение растворителя в объеме полимера неоднородно.

Различаются ограниченное и неограниченное набухание. Неограниченное набухание – это набухание, самопроизвольно переходящее в растворение. Если набухание не заканчивается растворением, оно называется ограниченным. Оно обусловленного ограниченным смешением линейного и разветвлённого строения с растворителем («плохой» растворитель), а так же наличием поперечных химических связей в полимере, что исключает разделение макромолекул и их переход в раствор.

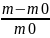Процесс ограниченного набухания характеризуется степенью набухания α= ; α=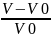 ; где-масса набухшего ВМС, -масса сухого ВМС,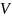 - количество поглощённой ВМС жидкости, отнесённое к еденице массы или объёма ВМС.α зависит от продолжительности процесса.

Скорость набухания может также характеризоваться углом наклона кривой зависимости степени набухания от времени к оси абсцисс: чем большеα, тем выше скорость. Уравнение для ограниченного набухания ВМС, скорость набухания 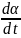= K(α_∞-α) K=constυ; ln(α_∞-α) =lnα_∞-Kt. Уравнение справедливо, если исходный полимер находится в высокоэластическом состоянии.

Степень набухания, которой соответствует появление горизонтального участка на кривой, называется максимальной или равновесной степенью набухания.

Форма кинетических кривых набухания зависит от структуры полимера, степени термодинамического сродства его к растворителю. При изменении внешних условий ограниченное набухание может перейти в неограниченное, и наоборот.

Образование соединения стехиометрического состава- «соединение набухания». Единицы растворителя образуют некоторые соединения с макромолекулами (целлюлоза-68% р-р HNO₃.Образуется соединение оксониевого типа 2С₆Н₁₀О₅* НNO₃). В растворе щелочи образуются алкоголяты целлюлозы CHClO₄ – 2C₆H₁₀O₅*HClO_4. Соединения набухания способны к кристаллизации.

Наряду с полиморфными превращениями происходит частичная декристаллизация ВМС. Возможно разрушение кристаллической структуры и неформирование новой( образуется аморфн. соед.) при внутри крист. набухании при нестехиометрическом набухании ВМС.

Микрокристаллическое набухание. Используют для пластификации ВМС и перевода аморфных зон из стеклообразного состояния в высокоэластичное.

Ацетилирование целлюлозы –медленно. Перед этим целлюлоза набухает в АсОН (межкристаллитное набухание). АсОНнаруш. ВС в молекуле целлюлозы и переводят ее в высокоэл. состояние.

Фракционирование. Разделение полимера на сравнительно узкие фракции и изучение их позволяет построить функцию распределения полимера в целом. Успех этого метода определяется правильным выбором условий фракционирования, позволяющих провести разделение полимолекулярного образца на возможно более узкие не перекрывающиеся фракции. Физический принцип фракционирования полимеров основан на зависимости их растворимости в критической области от величины молекулярной массы.

Два типа взаимодействия:

– взаимодействие «полимер - растворитель»;

– взаимодействие «полимер - полимер».

Разница в энергии взаимодействий «полимер - полимер» и «полимер - растворитель», зависящая от величины макромолекул, и позволяет проводить фракционирование.

В соответствии с теорией растворов полимеров Флори-Хаггинса

, (2.5.50)где φ2, φ1 = (1- φ2) - объёмные доли полимера и растворителя ,и , где z – число звеньев в макромолекуле (для гибких полимеров z соответствует степени полимеризации, z = Р); n1,n2- число молей растворителя и полимера; k– параметр Флори-Хаггинса, характеризующий разность энергий взаимодействия «полимер-полимер» и «полимер-растворитель».

Нарастание параметра k вплоть до некоторого критического значения kкр приводит к ограниченной растворимости полимера. При этом значении параметра взаимодействия начинается формирование второй фазы и при k >kкр раствор разделяется на две сосуществующие фазы. Такая критическая точка (экстремум) должна характеризоваться условиями

(2.5.51)(как любая экстремальная точка).

Учитывая условия (2.5.51) после двойного дифференцирования уравнения (2.5.50) можем получить для параметра

т.е. условия, необходимые для выпадения полимера из раствора с ухудшением качества растворителя определяются молекулярной массой полимера.

По мере уменьшения молекулярной массы kкр снижается, поэтому прежде всего из раствора будут выделяться фракции с большей молекулярной массой, а при экстракции будут растворяться фракции с меньшей молекулярной массой.

При добавлении осадителя по мере ухудшения качества растворителя раствор разделяется на две фазы. Распределение полимерных молекул между двумя растворами можно описать уравнением экспоненциального распределения Бренстеда-Шульце: , (2.5.53) где φ,φ¢- объемные доли полимера в разбавленном и концентрированном растворах; P – степень полимеризации распределенного полимера; s -сложная функция постоянной Флори-Хаггинса k, температуры, концентрации и т.д.

Эффективности фракционирования:

, (2.5.54)где φ P – доля молекул полимера со степенью полимеризации Р, остающихся в разбавленном растворе; Vφ, V'φ' – соответственно объемы разбавленного и концентрированного растворов; φ ,φ' – объемная доля полимера в разбавленном и концентрированном растворе; R = V'φ'/ Vφ.

. (2.5.55) позволяет оценить эффективность фракционирования и выявить ее зависимость от степени полимеризации (молекулярной массы).

Общие рекомендации по фракционированию.

-Доля полимера в разбавленном растворе тем больше, чем меньше отношение объемов осадка и раствора. Для качественного разделения необходимо снижать R.

-В осадке преимущественно будут накапливаться фракции с наибольшей молекулярной массой, так как чем больше R, тем меньше fP.

Однако это не означает, что другие фракции не будут переходить в осадок. Поэтому качественное разделение может быть достигнуто при повторном фракционировании первичных фракций.

-Для лучшего фракционирования следует применять минимальную концентрацию растворов (как правило, не более 1%).

-При выборе системы «растворитель-осадитель» необходимо подбирать такие компоненты, чтобы они смешивались и во всех соотношениях, во всем диапазоне рабочих температур. Необходимо следить, чтобы малые добавки осадителя не изменяли сильно качества растворителя и не выделяли больших количеств полимера.