Бубенщиков Сергей «Сравнение алгоритмов умножения матриц»

Оглавление

Постановка задачи 3

Теоретические сведения 4

Вводная часть 4

Классический алгоритм 4

Алгоритм Штрассена 4

Реализованные модели 8

Модель квадратной матрицы 8

Экспериментальная часть 10

План эксперимента 10

Условия проведения экспериментов 10

Характеристики компьютера: 10

Описание входных параметров 10

Результаты экспериментов 11

Выводы 14

Резюме 15

Список использованной литературы 16

Приложения 17

Приложение 1. Замеры времени, размерности 100 – 1200 17

Приложение 2. Замеры времени, размерности 500 – 4500 19

Приложение 3. Листинг 19

Класс Matrix 19

Оболочка для тестирования 24

Постановка задачи

Существует множество разнообразных алгоритмов умножения матриц. Одни алгоритмы более универсальны, другие обладают большей скоростью работы. В этой работе сравним скорость умножения квадратных матриц классическим алгоритмом и алгоритмом Штрассена.

Теоретические сведения

Вводная часть

Умножение матриц – одна из основных операций над матрицами. Умножать друг на друга можно только те матрицы, для которых число столбцов первого сомножителя равно числу строк второго сомножителя. Результатом умножения является матрица, у которой число строк равно числу строк первого сомножителя, а число столбцов совпадает с числом столбцов второго сомножителя [1].

В этой работе рассматривается умножение только квадратных матриц, т.е. матриц, у которых число строк и столбцов одинаково.

Классический алгоритм

Классический алгоритм умножения матриц отличается идейной простотой, и, как следствие, простотой программирования. Суть его заключается в следующем: для вычисления произведения двух матриц каждая строка первой почленно умножается на каждый столбец второй. Затем подсчитанная сумма таких произведений записывается в соответствующую клетку результата, т.е. , где n – размерность матриц.

Теоретическая оценка скорости работы классического алгоритма .

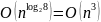Алгоритм Штрассена

Алгоритм Штрассена предназначен для быстрого умножения матриц [2]. Он был разработан в 1969 году. Штрассен был первым, кто показал возможность умножения матриц более эффективным способом, чем классическим.

Утверждение Штрассена: две матрицы размером 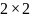можно умножить, используя 7 умножений и 18 сложений\вычитаний.

Пусть есть матрицы 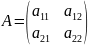, 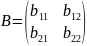. Тогда результат их произведения матрица , где:

• ;

• ;

• ;

• .

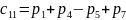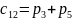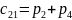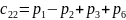Где, в свою очередь:

• ;

• ;

• ;

• ;

• ;

• ;

• .

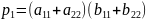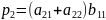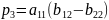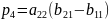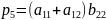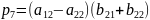Заметим: как сами формулы, так и их использование не требует, чтобы умножение элементов матриц было коммутативным. Это означает, что сами элементы могут быть матрицами, следовательно, алгоритм Штрассена можно применять рекурсивно. Для этого нужно представить матрицы-сомножители в виде матриц, состоящих из четырёх одинаковых матриц-блоков. Как следствие такого представления: алгоритм применим только к квадратным матрицам, размерность которых кратна степени двойки.

Для того чтобы воспользоваться алгоритмом Штрассена для умножения матриц, размер которых не соответствует степени двойки, необходимо расширить сомножители до размерности кратной следующей степени двойки, добавлением нулевых строк снизу и нулевых столбцов справа. Например: матрицу размерности пять следует расширить до размерности восемь.

Следствием такой зависимости алгоритма от конкретных размеров (кратных степени двойки) матриц является то, что для вычисления произведения матриц, размеры которых принадлежат отрезку 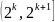, где , потребуется такое же время, как для матриц размера 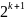. В результате, при построении графика зависимости времени работы алгоритма от размеров матриц, получим ступенчатую ломаную линию.

Предложение 1: при программной реализации учитывать количество ненулевых строк и столбцов матриц. Такой подход позволит обозначить нулевую матрицу. При умножении на такую матрицу возвращать такую же нулевую матрицу, а не выполнять излишнюю операцию умножения. Это актуально для больших, сильно расширенных матриц. Например: при умножении матриц размерности 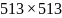придется расширить их до размерности 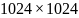, а далее умножать полученные сильно разреженные матрицы.

Даже после расширения матриц-сомножителей до размерности кратной степени двойки, алгоритм Штрассена асимптотически превосходит в скорости классический алгоритм.

Теоретическая оценка скорости работы алгоритма Штрассена .

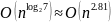Примечание: при программной реализации применение алгоритма Штрассена «в чистом виде»¹ может не дать превосходства в скорости над классическим алгоритмом из-за того, что алгоритм Штрассена основан на рекурсии. Рекурсия, в свою очередь, основана на многократном вызове процедуры, а вызов процедуры является весьма затратной, в плане времени, операцией.

Предложение 2: рекурсивные вызовы алгоритма производить до тех пор, пока матрицы-операнды не поместятся в кэш-память ЭВМ, а далее умножение осуществить классическим алгоритмом. Размер матриц, помещающихся в кэш-память, зависит от конкретной ЭВМ, но, как правило, это матрицы размерности порядка 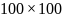элементов.

Такой подход позволяет сэкономить время за счёт сокращения числа рекурсивных вызовов и оптимального использования, более быстрой (по сравнению с оперативной памятью), кэш-памяти.

Замечание: в этой работе алгоритмом Штрассена называется его модификация, описанная в предложении 2.