Глава III

ДВИЖЕНИЕ В КОМБИНИРОВАННЫХ ПОЛЯХ

§ 13. Движение заряженных частиц

под действием однородного электрического

поля и однородного магнитного поля

Допустим, что направления электрического и магнитного полей совпадают. Ориентируем ось г вдоль направления полей и примем, что в начальный момент частица находится в точке О и обладает скоростью, составляющей угол а с осью г (рис. 13.1). Так же, как и в рассмотренном раньше случае, когда частица подвергалась воздействию одного магнитного поля, целесо­образно по отдельности рас­сматривать движение в пло­скости, перпендикулярной к оси 2, и движение вдоль оси 2. В перпендикулярной плоско­сти частица будет двигаться по окружности, радиус кото­рой определяется выраже­нием

(13.1)

Вдоль оси 2 движение будет равномерно ускоренным (или равномерно замедленным) с ускорением

Рис. 13.1. Составляющие начальной ско­рости частицы, движущейся в электри­ческом и магнитном полях, направления которых совпадают.

В результате траектория частицы будет представлять собой винтовую линию с переменным шагом (рис. 13.2 и 13.3).

Несколько более сложная картина возникает, если электри­ческое поле ориентировано под прямым углом к магнитному.

Направим ось у вдоль электрического поля, ось 2 — вдоль магнитного и предположим для простоты, что начальная ско­рость частицы лежи г в плоскости л;у. В таком случае вся

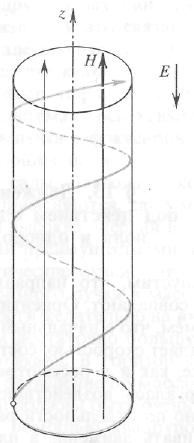
Рис. 13.2. Движение под действием

однородных полей. Векторы Е и Н

параллельны.

Рис. 13.3. Движение под действием

однородных полей. Векторы Е и Н

антипараллельны.

траектория частицы также "будет лежать в этой плоскости. Уравнения движения имеют вид

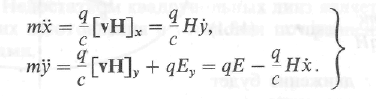
(13.3)

Наиболее быстрый и наглядный путь решения этих уравнений основан на замене переменных. Введем вместо х новую пере­менную х^ согласно формуле

(13.4)

где и — некоторая постоянная, Физический смысл такого преоб­разования состоит в переходе к новой системе координат, ко­торая движется относительно исходной со скоростью и в

направлении оси х. Уравнения (13.3) теперь перепишутся в сле­дующей форме:

(П.5)

Рели выбрать постоянную и равной

(13.6)

то второе из уравнений (13.5) упрощается, и система принимает следующий вид:

(13.7)

Электрическое поле бесследно исчезло из последних ра­венств, и они представляют собой, по существу, уравнения движения для частицы, находящейся под действием однород­ного магнитного поля. Таким образом, частица в новой системе

координат (хь у) должна двигаться по окружности. Так как эта новая система координат сама перемещается относительно ис­ходной со скоростью и = сЕ/Н, то результирующее движение частицы будет складываться из равномерного движения вдоль оси х и вращения по окружности в плоскости ху. Как известно, траектория, возникающая при сложении таких двух движений, в общем случае представляет собой трохоиду. На рисунке 13.4 приведены различные типы трохоид, соответствующие различ­ным по величине и направлению начальным скоростям частицы. В частности, если начальная скорость равна нулю, реализуется простейший случай движения такого рода — по циклоиде.

Другой интересный частный случай получается, если на­чальная скорость частицы направлена вдоль оси х и равна сЕ/Н. При этом трохоидальная траектория вырождается в прямую линию, так как в системе координат (хь у) частица

покоится. Заметим, что движение частицы под действием скре­щенных электрических и магнитных полей имеет общие черты с движением в неоднородном магнитном поле. В обоих случаях

результирующее движение скла­дывается из обращения по ок­ружности и поступательного пе­ремещения центра окружно­сти — так называемого дрейфа. Следует, однако, иметь в виду, что в отличие от дрейфа в неоднородном магнитном поле, где скорость дрейфа имеет про­тивоположное направление для различно заряженных частиц, в скрещенных полях направление дрейфа не зависит от знака заряда.

Нетрудно определить харак­тер движения частицы и в са­мом общем случае, когда элек­трическое и магнитное поля про­извольным образом ориентиро­ваны друг относительно друга. Выберем систему координат так, что ось 2 совпадает с направле­нием магнитного поля, а ось у

направлена вдоль составляющей электрического поля, перпен­дикулярной к магнитному (рис. 13.5). И в общем случае удобно рассматривать результирующее перемещение частицы как сло­жение двух более простых движений: в плоскости ху и вдоль оси 2, Проекция траектории на плоскость ху будет представ­лять собой трохоиду. Вдоль оси 2 частица будет двигаться рав­номерно ускоренно или равномерно замедленно. Результирую­щее движение изобразится довольно сложной пространственной кривой, которая для одного из частных случаев представлена на рис. 13,5.