
- •1. Что является объектом и предметом статистики? Каковы ее задачи?
- •2. Какие методы применяются в статистике?
- •3. Каковы этапы статистического исследования?
- •4. Каковы задачи и этапы проведения статистического наблюдения?
- •5. Какие существуют организационные формы, виды и способы статистического наблюдения?
- •6. Назовите виды статистических сводок и группировок и их место в системе статистических методов.
- •7. Какие существуют классификации статистических группировок?
- •8. Назовите существующие виды статистических таблиц и правила их построения.
- •9. Какие существуют виды статистических графиков и диаграмм.
- •10. Какие существуют виды статистических показателей, в каких формах они выражаются?
- •11. Каковы сущность и значение относительных показатели структуры, координации, динамики?
- •12. Каковы сущность и значение относительных показателей напряженности и выполнения плана, сравнения, интенсивности?
- •13. Как производятся расчеты средних: арифметической и гармонической, простых и взвешенных?
- •14. Как рассчитываются простые и взвешенные средние: геометрическая и квадратическая?
- •15. Как определяются размах вариации, среднее линейное отклонение?
- •16. Какие существуют методы расчета дисперсия, среднего квадратического отклонения, коэффициент вариации?
- •17. Назовите структурные показатели вариационного ряда, показатели дифференциации.
- •18. Какими методами определяются абсолютные относительные, базисные и цепные уровни изменения ряда динамики?
- •19. Как исчисляются коэффициенты (индексы) роста, темпы роста, темпы прироста, абсолютное значение одного процента прироста?
- •20. Порядок расчетов среднего абсолютного прироста, среднего коэффициента роста и среднего темпа прироста?
- •21. Дайте определение, что такое индекс и приведите классификацию индексов.
- •22. Как определяется индексы: цен, физического объема, товарооборота?
- •23. Как рассчитываются индексы: средней цены переменного состава, средней цены постоянного состава, структурных сдвигов.
- •24. Назовите важнейшие экономические индексы и их взаимосвязи.
- •25. Причинность, регрессия, корреляция. Основные задачи и предпосылки применения корреляционно-регрессионного анализа.
- •2 Типа взаимосвязей между х и у:
- •26. Корреляционные параметрические методы изучения связи.
- •27. Коэффициент парной корреляции. Оценка его значимости.
- •28. Парная регрессия на основе метода наименьших квадратов и метода группировки.
- •29. Оценка существенности связи. Прогнозирование на основе регрессионных моделей.
- •30. Коэффициенты ассоциации и контингенции.
- •31. Коэффициенты взаимной сопряженности.
- •32. Ранговые коэффициенты корреляции.
- •33. Общие принципы исчисления показателей продукции. Классификация производства.
- •34. Какие основные элементы составляют продукцию промышленности?
- •35. Назовите основные показатели промышленной продукции.
- •36. В каких случаях применяются натуральные показатели?
- •37. Как определяются численность и состав работников?
- •38. Движение рабочей силы и его показатели.
- •39. Какой существует порядок определения рабочего времени и показатели его использования.
- •40. Назовите формы и системы оплаты труда.
- •41. Каков состав фонда заработной платы?
- •42. Какие существуют показатели уровня и динамики заработной платы? Порядок их расчета.
- •43. Какие существуют виды и показатели прибыли?
- •44. Что означает показатель рентабельности и какие показатели рентабельности Вы знаете?
- •45. Какая взаимосвязь имеется между показателями рентабельности и оборачиваемости средств?
14. Как рассчитываются простые и взвешенные средние: геометрическая и квадратическая?
Лекция 3
Средние диаметры колес, труб, средние стороны квадратов определяются при помощи средней квадратической.
Среднеквадратические величины используются для расчета некоторых показателей, например коэффициент вариации, характеризующего ритмичность выпуска продукции. Здесь определяют среднеквадратическое отклонение от планового выпуска продукции за определенный период по следующей формуле:
![]()
Эти величины точно характеризуют изменение экономических показателей по сравнению с их базисной величиной, взятое в его усредненной величине.
Средняя квадратическая применяется в тех случая, когда исходные значения X могут быть как положительными, так и отрицательными, например при расчете средних отклонений.
![]()
Квадратическая простая
Средняя квадратическая простая вычисляется по формуле:
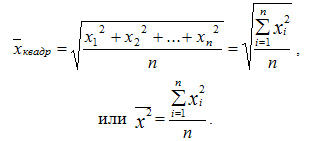
Квадратическая взвешенная
Средняя квадратическая взвешенная равна:
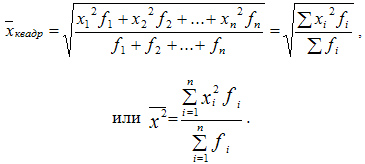
Средняя геометрическая применяется при определении средних относительных изменений, о чем сказано в теме Ряды динамики. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения X, который был бы равноудален как от максимального, так и от минимального значения X.
![]()
Среднегеометрическая величина дает возможность сохранять в неизменном виде не сумму, а произведение индивидуальных значений данной величины. Ее можно определить по следующей формуле:
![]()
Среднегеометрические величины наиболее часто используются при анализе темпов роста экономических показателей.
Геометрическая простая
Для расчетов средней геометрической простой используется формула:
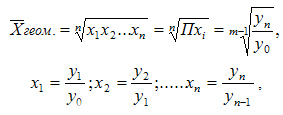
где:
— цепной коэффициент роста
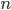 —
число
этих коэффициентов роста
—
число
этих коэффициентов ростаП — знак произведения
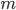 —
количество
уровней ряда
—
количество
уровней ряда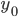 —
значение
начального уровня ряда
—
значение
начального уровня ряда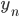 —
значение
конечного уровня ряда
—
значение
конечного уровня ряда
Геометрическая взвешенная
Для определения средней геометрической взвешенной применяется формула:
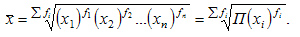
15. Как определяются размах вариации, среднее линейное отклонение?
Стр. 23-25 в методичке
Размах
вариации. Все признаки, отмеченные в
статистике, подвержены колебанию. Самым
простым показателем такой колеблимости
любого признака является размах вариации.
В общем случае он представляет собой
разность между наибольшим и наименьшим
значением признака. Размах вариации
зависит от двух значений признака, что
в экономике означает неточность
определения. Среднее
линейное отклонение. Измерителем
среднего линейного отклонения считается
величина отклонений от средней, взятых
без учета алгебраического знака.
Исчисленная таким образом величина
среднего отклонения называется средним
линейным отклонением. В практике следует
иметь в виду, что величины линейного
отклонения различных вариационных
рядов можно сравнить лишь в том случае,
если эти ряды характеризуются примерно
одинаковыми средними. А т.к. это бывает
в практике не всегда, то для сопоставления
колеблимости исчисляются относительные
показатели колеблимости, т.е. относят
линейные отклонения к арифметической
средней. Используя ранее принятые
обозначения варьирующего признака,
веса и средней, можно порядок расчета
среднего линейного отклонения записать
в виде формулы![]() .
Но в случае, если варианты в распределении
признака не повторяются, то среднее
линейное отклонение рассчитывается по
следующей формуле:
.
Но в случае, если варианты в распределении
признака не повторяются, то среднее
линейное отклонение рассчитывается по
следующей формуле:![]()
