26. Корреляционные параметрические методы изучения связи.

Корреляционные параметрические методы - методы оценки тесноты свози, основанные на использовании, как правило, оценок нормального распределения, применяются в тех случаях, когда изучаемая совокупность состоит из величин, которые подчиняются закону нормального распределения.

Параметризация уравнения регрессии: установление формы зависимости; определение функции регрессии; оценка значений параметров выбранной формулы статистической связи Методы изучения связи - форму зависимости можно установить с помощью поля корреляции. Если исходные данные (значения переменных х и у) нанести на график в виде точек в прямоугольной системе координат, то получим поле корреляции При этом значения независимой переменной x (признак-фактор) откладываются по оси абсцисс, а значения результирующего фактора у откладываются по оси ординат. Если зависимость у от x функциональная, то все точки расположены на какой-то линии. При корреляционной связи вследствие влияния прочих факторов точки не лежат на одной линии.

Расчет показателей силы и тесноты связей Линейный коэффициент корреляции - количественная оценка и мера тесноты связи двух переменных. Коэффициент корреляции принимает значения в интервале от -1 до +1. Считают, что если этот коэффициент не больше 0,30, то связь слабая: от 0,3 до 0,7 - средняя; больше 0,7 - сильная, или тесная. Когда коэффициент равен 1, то связь функциональная, если он равен 0, то говорят об отсутствии линейной связи между признаками.

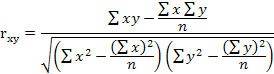
Коэффициент детерминации - квадрат линейного коэффициента корреляции, рассчитываемый для оценки качества подбора линейной функции.

Формула нелинейного коэффициента корреляции:

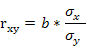
Корреляция для нелинейной регрессии Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем корреляции, а именно - индексом корреляции (R):

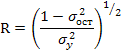
где  - общая дисперсия результативного признака у,   - остаточная дисперсия, определяемая исходя из уравнения регрессии : ух = f(х). Корреляция для множественной регрессии. Значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата - коэффициента детерминации. Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или оце­нивает тесноту совместного влияния факторов на результат. Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:

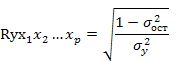
где   - общая дисперсия результативного признака;

 - остаточная дисперсия для уравнения

у = f (x₁,x₂,…,x_p)

27. Коэффициент парной корреляции. Оценка его значимости.

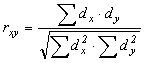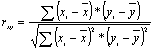Коэффициент парной корреляции вычисляется по формуле:   или  Алгоритм расчета коэффициента парной корреляции:  1)     записывают исходные данные в два вариационных ряда – x и y;  2)     вычисляют среднюю арифметическую ряда x и y;  3)     определяют разность между членом ряда и средними величинами;  4)     перемножают разности ряда x и y между собой;  5)     находят сумму перемножаемых разностей (с учетом арифметического знака);  6)     возводят в квадрат каждую разность (отклонение) ряда х и у;  7)     определяют сумму квадратов отклонений (разностей) для ряда х и у отдельно;  8)     подставляют полученные данные в исходную формулу и вычисляют коэффициент парной корреляции. 

коэффициент парной корреляции, г (product moment correlation г), который характеризует степень тесноты связи между двумя метрическими (измеряемыми с помощью интервальной или относительной шкал) переменными, скажем, X и Y. Этот коэффициент используют, чтобы определить, существует ли между переменными линейная зависимость. Он показывает степень, в которой вариация одной переменной Х связана с вариацией другой переменной Y, т.е. меру зависимости между переменными Xvl Y