Раздел «Начертательная геометрия»

1. В чем заключается метод ортогонального проецирования?

Метод проецирования заключается в том, что любая точка пространства может быть спроецирована с помощью проецирующих лучей на любую поверхность. Ортогональное проецирование это такой метод когда проецирующие лучи параллельны между собой и перпендикулярны к плоскости проекций.

2. Какие прямые называются проецирующими? Какие их основные особенности?

Прямые перпендикулярные к какой-либо координатной плоскости называются проецирующими прямыми.

Они делятся на горизонтально-проецирующие, фронтально-конкурирующие, профильно-проецирующие. Проецирующие прямые имеют два важных свойства: во первых они параллельны двум координатным плоскостям и значит на эти плоскости они проецируются в натуральную величину; и второе - на плоскость к которой они перпендикулярны они проецируются в точку (вырождаются в точку, собирают все точки в одну точку), что упрощает решение многих задач встречающихся в начертательной геометрии и, соответственно, в практике задач.

3. Каким способом можно определить длину (нв – натуральную величину) отрезка прямой?

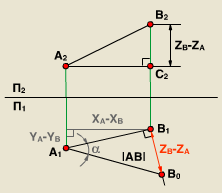
Графически на чертеже эту задачу решают по схеме:

1 Обозначить вторую проекцию С2 точки С;

2 Определить длину отрезка В2С2, как разность глубин точек А и В относительно П1.

3 На плоскости П1 из точки В1 провести прямую отрезку А1В1 и на этой прямой отложить отрезок В1B0, равный В2С2. Получится прямоугольный треугольник А1В1B0.

4 Гипотенуза А1B0 прямоугольного треугольника А1В1B0 равна натуральной величине отрезка АВ, а угол a - угол наклона отрезка АВ к фронтальной плоскости проекций.

4. Как определить углы наклона отрезка прямой к плоскостям проекций?

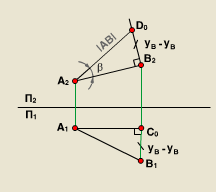
Графически на чертеже эту задачу решают по схеме:

1 Обозначить вторую проекцию с2 точки с;

2 Определить длину отрезка В2С2, как разность глубин точек А и В относительно П1.

3 На плоскости П1 из точки В1 провести прямую отрезку А1В1 и на этой прямой отложить отрезок В1B0, равный В2С2. Получится прямоугольный треугольник А1В1B0.

4 Гипотенуза А1B0 прямоугольного треугольника А1В1B0 равна натуральной величине отрезка АВ, а угол a - угол наклона отрезка АВ к фронтальной плоскости проекций.

Аналогично, тот же алгоритм можно проделать, проведя отрезок АС || А2В2, т. е. || П2, и построив на ортогональном чертеже натуральную величину отрезка АВ на плоскости П1, в этом случае возможно определить угол b - угол наклона отрезка АВ к горизонтальной плоскости проекций.

5. Как определить пересекающиеся или скрещивающиеся прямые? Какие точки называются конкурирующими?

Пересекающимися называются две прямые лежащие в одной плоскости и имеющие одну общую точку.

Если прямые пересекаются, то точки пересечения их одноименных проекций находится на одной линии связи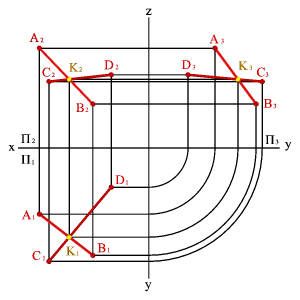

Скрещивающимися называются две прямые не лежащие в одной плоскости.

Если прямые не пересекаются и не параллельны между собой, то точка пересечения их одноименных проекций не лежит на одной линии связи.

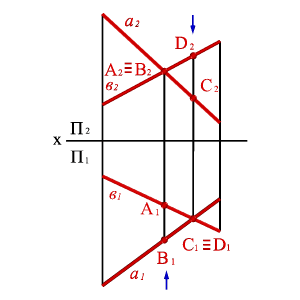
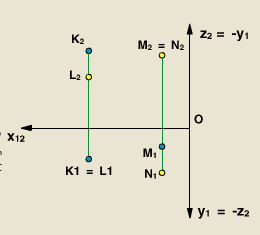
Точки, у которых проекции на П1 совпадают, называют конкурирующими по отношению к плоскости П1, а точки, у которых проекции на П2 совпадают, называют конкурирующими по отношению к плоскости П2.

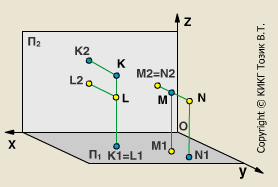
Точки К и L конкурирующие по отношению к плоскости П1, так как на плоскости П1 точки К и L проецируются в одну точку: К1 = L1. Точка К выше точки L, т.к. К2 выше точки L2, потому К1 на П1 видима.

Точки N и М конкурирующие по отношению к плоскости П2, так как на плоскости П2 точки M и N проецируются в одну точку: М2 = N2. Точка N ближе к наблюдателю, чем точка М, т.к. координата у точки N больше, чем у точки М, а потому точка N закрывает точку М, а потому N1 на П2 является видимой.