2.3 Раскрытие неопределенностей при вычислении пределов алгебраических функций

1. Чтобы раскрыть неопределенность 0/0 в случае отношения многочленов при x a, следует в числителе и знаменателе выделить общий множитель вида (x-a) и на него сократить, т.к. (x-a) не равно 0, под знаком предела x a, но никогда не достигает.

2. Чтобы раскрыть неопределенность 0/0 в случае отношения иррациональных функций, следует выделить общий множитель вида (x-a) не равный нулю путем переноса иррациональности из числителя в знаменатель или из знаменателя в числитель, умножением на сопряженное выражение как числителя так и знаменателя.

Выражение называется сопряженным данному иррациональному выражению, если их произведение равно рациональному выражению.

Иррациональное выражение	Сопряженное выражение	Результат

3. Чтобы раскрыть неопределенность при , следует числитель и знаменатель поделить почленно на бесконечно большую более высокого порядка (если входят степенные функции, то на высшую степень переменной).

4. Чтобы раскрыть неопределенность , следует привести ее к виду или путем приведения к общему знаменателю или умножением на сопряженные выражения.

2.4 Первый замечательный предел

Первым замечательным пределом называют предел

□ Построим единичную окружность и отметим точки ОАВС как на рисунке 2.3.

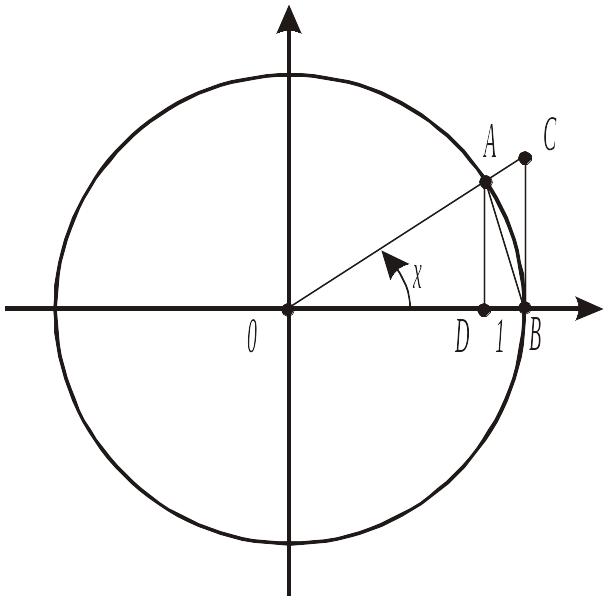
Рисунок 2.3 - К доказательству первого замечательного предела

Пусть сначала . Площадь сектора ОАВ больше, чем площадь треугольника ОАВ, но меньше площади треугольника ОСВ .

Найдем эти площади , , . Подставим эти площади в неравенство. .

Разделим все части неравенства на . Так как знак неравенств не изменится . Отсюда следует: . , , тогда по теореме о сжатой переменной и .

Пусть теперь , , , поэтому выполняется то же равенство.

■



○

2.5 Определение левого и правого пределов функции. Связь предела функции с односторонними пределами

Собственная точка называется левой (правой) предельной точкой множества , если в любой окрестности точки слева (справа) от точки найдутся точки множества отличные от .

Пусть - левая (правая) предельная точка множества . Число - собственное или несобственное называется левым (правым) пределом функции в точке , если

- левый предел

- правый предел



,

○

Теорема (о связи предела функции с односторонними пределами)

Пусть точка являющаяся предельной точкой множества является одновременно и левой и правой предельной точкой множества . Тогда для существования предела функции в точке , равного , необходимо и достаточно существование односторонних пределов функции в точке , и равенство их числу .

(2.7)

; (2.8)

; (2.9)

□ Необходимость

Пусть существует , это значит (по определению), что выполняется условие (2.7). Требуется доказать, что , т.е. выполняется (2.9).

Возьмем - произвольное и найдём такое, что .

Для этого (по взятому ) найдём число из выполнения (2.7) ( ). Положим , такое - искомое: если для точки выполняется , то , а в этом случае , ч.т.д. существует правый предел и он равен .

Аналогично можно доказать, что если , то левый предел, т.е. выполняется условие (2.8).

Достаточность

Пусть существует , т.е. выполняется (2.8) (2.9). Требуется доказать что , т.е. выполняется (2.7).

Возьмем - произвольное. По этому числу найдём из выполнения условия (2.8) , . Для этого же найдётся по условию (2.9) . Положим , это - искомое т.к. выполняется либо , .

■