1.4 Тригонометрическая и показательная форма записи комплексных чисел

Модулем комплексного числа называется действительное положительное число . (1.2)

Аргументом комплексного числа называется угол , между действительной осью комплексной плоскости и вектором .

Для вычисления аргумента комплексного числа можно использовать формулу:

(1.3)

С использованием понятий модуля и аргумента комплексное число записывается в тригонометрической форме:

(1.4)



,

, ,

,

,

.

○

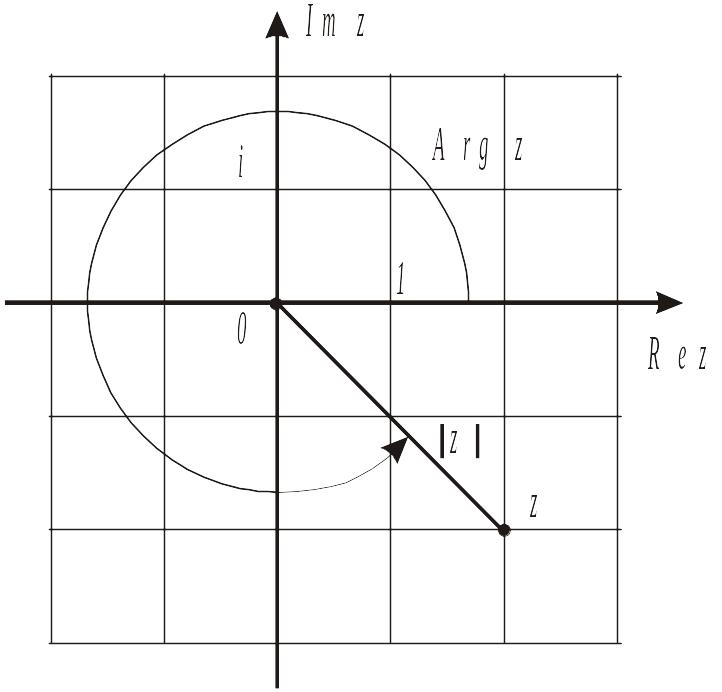
Рисунок 1.6 - Тригонометрическая форма записи комплексного числа

Если комплексные числа заданы в тригонометрической форме, то особенно удобно выполнять операции умножения, деления и возведения в степень:

Если , , то

, (1.5)

, (1.6)

. (1.7)

Еще одной формой записи комплексного числа является показательная форма, которая была получена Эйлером и носит название формулы Эйлера:

(1.8)

Из формулы Эйлера можно получить комплексные формулы для синуса и косинуса числа:

, . (1.9)

1.5 Корень из комплексного числа

Определение корня для комплексных чисел такое же, как и для действительных чисел.

Число называется корнем степени n из комплексного числа , если .

Выведем формулу для вычисления корня.

Пусть число в тригонометрической форме имеет вид , тогда

.

Сравним с . Эти числа должны быть равны. Для этого должно совпадать

,

, , , , .

.

. (1.10)



Вычислить , .

,

,

.

.

,

,

,

,

,

.

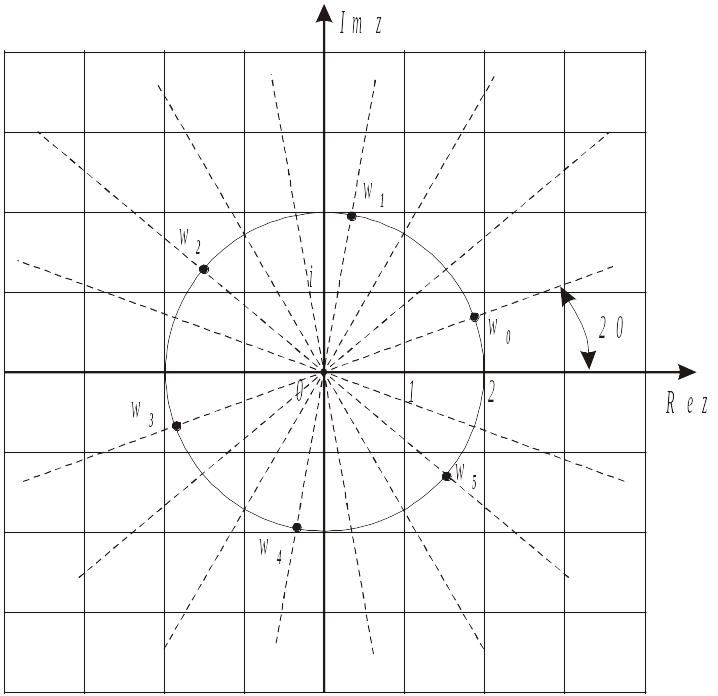
Рисунок 1.7 - Корень из комплексного числа

○

Имеется ровно корней из комплексного числа степени . На комплексной плоскости все корни лежат на окружности радиуса , делят окружность на равных частей. Первый корень отстоит на угол от положительного направления действительной оси.



Решить уравнение неполное уравнение третьей степени.

+3i=0

○



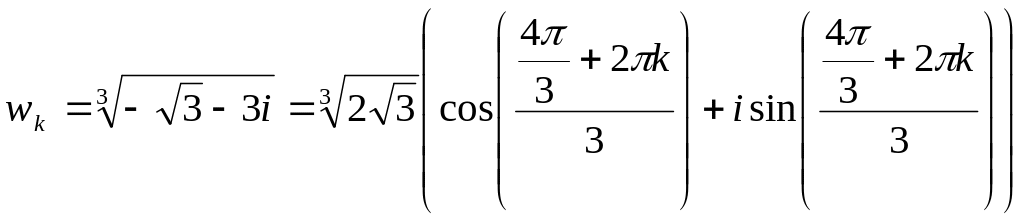
Для комплексных чисел справедливы формулы решения квадратных уравнений через вычисление дискриминанта

Корни квадратного уравнения с отрицательным дискриминантом - комплексно сопряженные числа, расположены симметрично относительно действительной оси (рисунок 1.8).

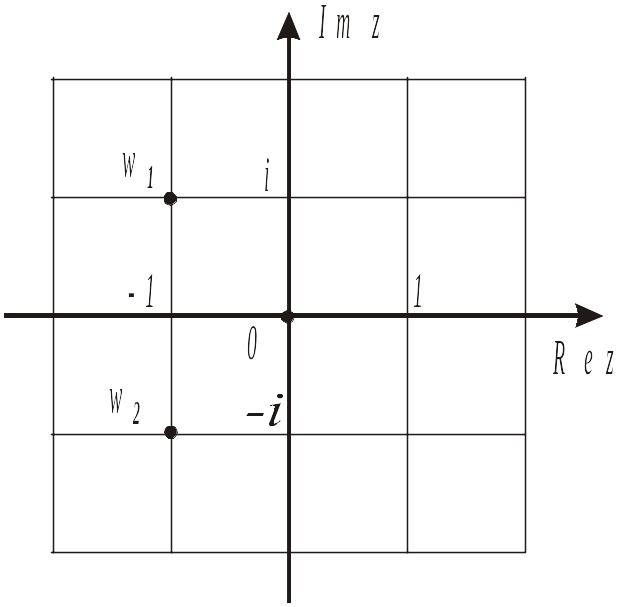
Рисунок 1.8 - Корни квадратного уравнения с отрицательным дискриминантом

○

1.6 Функции. Основные определения.

Пусть имеются множества и .

Если каждому элементу ставится в соответствие единственный элемент (его обозначают ), то говорят, что на множестве задана функция со значениями на множестве .

- называют образом элемента , а элемент - прообразом элемента .

Множество называют областью определения функции. Область определения функции обозначается .

Все значения, которые может принимать функция называются множеством значений функции. Множество значений функции обозначается .



Пусть дана числовая функция (график приведен на рисунке 1.9).

Для , число является образом.

В свою очередь для , число - прообраз.

Множество определения данной функции:

, , .

Множество значений данной функции:

, .

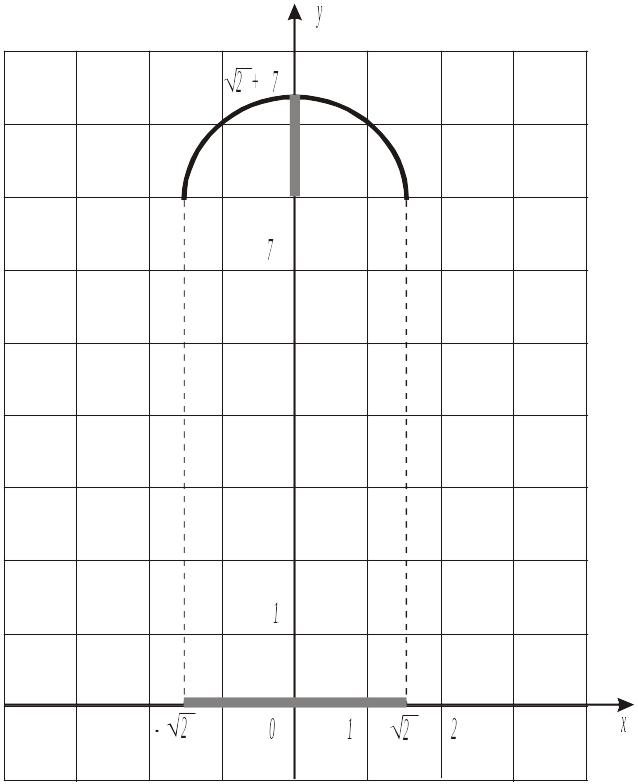
Рисунок 1.9 - График функции

○

Множество может быть шире, чем область значений функции.

Если множества и - числовые, то функция называется числовой.

Функция действующая из множества натуральных чисел на множество действительных чисел называется последовательностью.

Значения этой функции при значении аргумента называется -ым членом последовательности и обозначается .

Таким образом, последовательность – частный случай функции.



,

○

Функция называется взаимно однозначной или биекцией, если для каждого значения существует только один образ , и для каждого только один прообраз .

Пусть имеется биекция, , тогда функция, ставящая каждому элементу , его прообраз называется обратной функцией и обозначается .



, .

Пусть имеются функции, и , тогда функция ставящая каждому элементу , элемент называется суперпозицией функций и или сложной функцией.

○



, , .

○