Содержание

1 Элементы теории множеств 2

1.1 Понятие множества. Способы задания множеств. Операции над множествами 2

1.2 Основные числовые множества 3

1.3 Комплексные числа. Алгебраическая форма записи комплексных чисел 4

1.4 Тригонометрическая и показательная форма записи комплексных чисел 7

1.5 Корень из комплексного числа 8

1.6 Функции. Основные определения. 10

1.7 Способы задания функций. Элементарные функции и их свойства. 12

1.8 Ограниченность функций 15

2 Предел числовой функции 16

2.1 Окрестности собственных и несобственных точек. Предельные точки множества. Предел функции. 16

2.2 Свойства и вычисление пределов 17

2.3 Раскрытие неопределенностей при вычислении пределов алгебраических функций 19

2.4 Первый замечательный предел 20

2.5 Определение левого и правого пределов функции. Связь предела функции с односторонними пределами 21

2.6 Теорема о пределе монотонной функции 22

2.7 Предел последовательности. Второй замечательный предел 22

2.8 Сравнение функций. 24

3. Непрерывность числовой функции одной переменной 27

3.1 Непрерывность функции в точке и на промежутке 27

3.2 Точки разрыва функции 28

3.3 Свойства функций, непрерывных в точке и на отрезке 29

1 Элементы теории множеств

Математический анализ – часть фундаментальной математики, изучающая числовые функции.

1.1 Понятие множества. Способы задания множеств. Операции над множествами

Множество – первичное неопределяемое понятие, обозначающее набор некоторых элементов.

Для обозначения множеств используются прописные буква латинского алфавита, элементы множества обозначают строчными буквами латинского алфавита.

Если множество содержит элемент , то говорят, что элемент принадлежит множеству , и пишут .

При описании множеств используются следующие логические знаки:

- квантор общности,

- квантор существования,

- импликация (следование),

- эквиваленция (равносильность).



- для любого элемента , принадлежащего множеству , выполняется свойство .



- существует такой элемент , принадлежащий множеству , для которого выполняется свойство .



- если выполняется свойство , то выполняется свойство . - необходимое условие для . - достаточное условие для .



- если выполняется свойство , то выполняется свойство и наоборот, если выполняется свойство , то выполняется свойство .

Условие является необходимым и достаточным для условия . И наоборот: условие является необходимым и достаточным для условия .

Другими словами - условие является критерием для выполнения условия . И наоборот: условие является критерием для выполнения условия .

Для задания множества используют следующие способы:

1. словесное (вербальное) описание множества,

2. перечисление элементов,

3. характеристическое свойство элементов множества.



Одно и тоже множество может быть описано разными способами

1. «Множество натуральных делителей числа 12»,

2. ,

3. , такие натуральные числа , для которых выполняется свойство: частное 12 и - натуральное число.

○

Универсальным множеством или универсумом называют множество, содержащие любые элементы.

Пустым множеством называют множество, не содержащее элементов.

Равенство двух множеств обозначает, что любой элемент из первого множества принадлежит второму и наоборот: означает, что .

Множество является подмножеством множества , , если каждый элемент множества принадлежит множеству : .

Числовым множеством называют множество, элементами которого являются числа.

Над множествами выполняют следующие основные операции: объединение, пересечение, разность, дополнение, декартово произведение.

Объединением множеств и называется множество , каждый элемент которого принадлежит хотя бы одному из множеств или .

Пересечением множеств и называется множество , каждый элемент которого принадлежит и и .

Разностью множеств и называется множество , каждый элемент которого принадлежит , но не принадлежит .

Если множество является подмножеством множества , то дополнением множества до множества называется множество , каждый элемент которого принадлежит , но не принадлежит . Если в роли множества выступает универсальное множество, то дополнение обозначается .

Леонард Эйлер предложил изображать множества - пересекающимися кругами, а универсум - квадратом (или прямоугольником). Полученные диаграммы называют диаграммами Эйлера, они позволяют наглядно изображать результаты действий над множествами (рисунок 1.1).

Декартовым произведением множеств и называется множество , каждый элемент является парой, первый элемент которой принадлежит , а второй принадлежит :

.

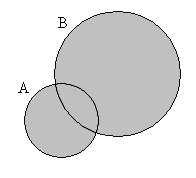
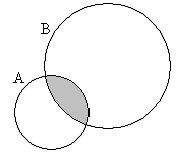
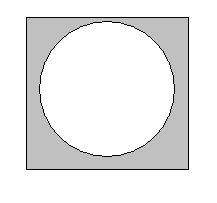
Рисунок 1.1 - Диаграммы Эйлера для операций над множествами



Пусть - множество делителей числа 12, а - множество делителей числа 15: , . Тогда

, , , .

○