Вопрос 20

Зависимости между логическими операциями

Операции не являются независимыми; одни из них могут быть выражены через другие. Можно доказать с помощью таблиц истинности следующие равносильности:

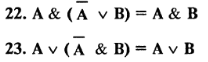
Одну и ту же зависимость между логическими переменными можно выразить различными формулами. Поэтому важно иметь возможность приводить формулы с помощью эквивалентных преобразований к некоторому стандартному виду. Существует несколько стандартных форм, к которым приводятся логические выражения с помощью эквивалентных преобразований (формул 1—23).

Первая из них — дизъюнктивная нормальная форма (ДНФ), имеет вид: где каждое из составляющих высказываний есть конъюнкция простых высказываний и их отрицаний, например:

Вторая — конъюнктивная нормальная форма (КНФ), имеет вид: где каждое из составляющих есть дизъюнкция простых высказываний и их отрицаний, например: