1. Равновесныеинеравновесныеносителизаряда

1. Равновесныеносителизарядавполупроводниках

Вучебникахпофизикеполупроводников[6.1–6.4]показано,чтовкристалледляэлектронасуществуютразрешенныезоны,вкоторыхэнергияэлектронаизменяетсянепрерывновзависимостиотквазиим-пульса.Приэтомчастьзон(валентнаязона)приТ=0полностьюза-

полненаэлектронами,ачастьзон,отделеннаяотвалентнойзоныза-прещеннымпромежутком(зонапроводимости),пустая.Еслитемпера-тураотличнаотнуля,точастьэлектроновизвалентнойзоныперехо-дитвзонупроводимостиикаким-тообразомраспределяетсяпоэнергии.Такиежепереходымогутосуществлятьсяиприпоглощениисвета.Вэтомпараграфебудетрассмотрено,какименнораспределяют-сяразрешенныеквантовыесостояниявпространствеквазиимпульсовикакимобразомраспределяютсяэлектроныпоэтимсостояниям.

Привычисленииразрешенныхсостоянийиспользуетсяпредстав-

лениеофазовомпространстве,т.е.пространстве,заданномзначениями

энергииэлектронаиегоквазиимпульса.Можнопоказать,чторазре-шенныезначениякомпонентовквазиимпульсаобразуютдискретнуюсовокупностьсоченьмалымиразностямимеждусоседнимизначения-

ми.Этаразностьравна^{2},гдеL–размеркристалла,иэтопозволя-

L

етнайтиплотностьразрешенныхсостоянийвпространствеквазиим-пульсов.В[6.1–6.4]плотностьсостояний,(g(P)),приходящаясяна

единицуквазиимпульса(P)инаединицуобъемавещества,опреде-ляетсякак

^gP^dP

4P²dP

.

_h3

Впростейшемслучаедлясферическойзоныкинетическаяэнергияэлектронавсоответствиис[6.1]можетбытьзаписанакак

2_{k2 P}2

E(k)  .

2m^

2m^

Тогдазависимостьплотностиэлектронныхсостоянийотэнергииможетбытьвыраженаввиде:



32



g_E_dE4_^2m

^EE

^{12dE. (6.1.1)}

_h^{2 c}

 

Уравнение(6.1.1)определяет

g(E)

какдляэлектроноввзонепро-

водимости,такидлядырокввалентнойзонеприсоответствующем

выбореэнергии.Дляслучая,когдазонынесферические,т.е.эффек-

тивнаямассаявляетсятензором,зависимость

g(E)имеетвид





^13²³² 12

^{gEdE4}_^m_x^m_y^m_z

_2

h

^EE_c

dE,

где

x y z

m^,m^,m^–главныемассывдольнаправленияортогональных

осей.

Энергияэлектрона(какизоннаяструктуракристаллавцелом)мо-жетотображатьсякаквEk-координатах,такивEх-координатах,когдаизображаютсяпространственныезависимостидназоныпрово-димостиивалентнойзоны,азазормеждунимиотображаетзапрещен-нуюзону.

РаспределениеэлектроновпоразрешеннымквантовымсостояниямосновываетсянапринципеПаулиистатистикеФерми–Дирака.Прин-ципПаулизаключаетсявутвержденииотом,чтодваэлектронавато-менемогутнаходитьсяводномквантовомсостоянии.ФермииДиракраспространилиэтотпринципнаэлектроны,находящиесявлюбойсистеме:вансамблеэлектроновнеможетбытьдвухэлектроновсоди-наковымнаборомквантовыхчисел.ФункцияраспределенияФерми–Дирака,полученнаянаосновеэтогопринципа,записываетсякак

^fE,T^

1e

1

EE_F

kT

, (6.1.2)

гдеk–постояннаяБольцмана;T–температура;E_F

–уровеньФерми.

Функцияраспределенияотражаетвероятностьтого,чтопритепло-вомравновесиивсистеменеразличимыхчастиц(вданномслучаеэлектронов)состояниесэнергиейEзанято.Соответственно,вероят-ностьтого,чтосостояниесэнергиейEнезаполнено,равна1f(E,T).УровеньФермиможноопределитькакизменениесвобод-

нойэнергиисистемы,находящейсяприпостояннойтемпературеиимеющейпостоянныйобъем,придобавленииодногоэлектрона.ВполупроводникахуровеньФермипредставляетсобойхарактернуюэнергию,зависящуюоттемпературы,объема,концентрацииэлектро-новвзонепроводимости,наличиялокальныхцентровипр.Кромето-го,каквидноиз(6.1.2),уровеньФермиможноопределитькакэнергию

такогоквантовогосостояния,вероятностьзаполнениякоторогоравнаоднойвторой.

ЕсливполупроводникеуровеньФермирасполагаетсянижедназо-

ныпроводимости(иливышепотолкавалентнойзоны)неменеечемна^{несколькоk}T^{,тотакойполупроводник(иэлектронныйгаз)называет-ся}невырожденным,араспределениеФерми–Диракапереходитврас-

E_FE

пределениеМаксвелла–Больцмана

^fE,T^ekT

.Впротивополож-

номслучаеполупроводникназываетсявырожденным.Такимобразом,еслиуровеньФермивполупроводникезафиксирован,товероятностьнахожденияэлектронанауровнесопределеннойэнергиейэкспонен-циальнопадаетсувеличениемэнергииэтогоуровняили,другимисло-вами,электронызаполняютнижниеуровни.

Концентрацияэлектроноввзонепроводимостивыражаетсячерезплотностьсостоянийифункциюраспределенияследующимобразом:



n_

E_C

^gE^{fE,TdEN}_C^_1/2^{(), (6.1.2а)}

_ 2^

x¹²dx

EE_C

_ 

где

^1/2^

_ _

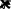^01e

;

_x^_

x ;

kT

E_F_C;_kT;

32

 ^ 

_{N2}2m_nkT_

–эффективнаяплотностьсостоянийвзонепро-

C ^^2^2

 

водимости.

Длярасчетовполезнознатьприведеннуюформулудляплотностисостояний:

_m

32 ₃₂



_19n,p

^T ₃

N_C,v2,510^_m ^

^300^

,см

, (6.1.3)

 _{0  }

 

гдеm_0массасвободногоэлектрона.

ПоложениеуровняФермиводнородномполупроводникеопреде-ляетсяизусловийнейтральности:вобъемеполупроводникаконцен-трациявсехотрицательныхзарядовдолжнаравнятьсяконцентрациивсехположительныхзарядов.Длясобственногополупроводника,где

нетнидоноров,ниакцепторов,условиенейтральностисводитсякра-венствуконцентрацийэлектроновидырок:

n_0p_0n_i

^NN0,5

_eE_g

2kT

, (6.1.4)

гдеE_g

Cv

–шириназапрещеннойзоныполупроводника.

Вполупроводнике,вкотороместьдонорыи(или)акцепторы,ус-ловиенейтральностизаписываетсядлявсехзарядов:свободныхэлек-троновидырок,ионизованныхакцепторовидоноров(n_a,p_d),концен-трациякоторыхсоответственноравна:

N

n_a ^a

N

; p_d ^d ,

exp^{EaEF}1 exp^{EFEd}1

^ kT

  _kT 

где

N_a,N_d

   

–концентрацияакцепторовидоноров,а(E_aE_F)и

(E_FE_d)–расстояниемеждуакцепторнымуровнемиуровнемФермииуровнемФермиидонорнымуровнем.

_Е,эВ Е,эВ

^ЕС

Е,эВ

0,02 Е_F

1,1

1,0

Е_С–0,01 Е_d

Е_С–0,02 ^Е_F

^{0,01 Е}а

₀ Е_v

0,9

0,8

0,7

0,6

0,5

0,4

0,3

0,2

0,1

0

Е_С

Е_d

^ЕFi

010203040Т,К

Е_F

^ЕС 010203040Т,К

^ЕFi

Е_F

Е_а

–0,1

–0,2

Е_v

0 100200300400500

Т,К

Е_v

0 100200300400500

Т,К

а б

Рис.6.1.ЗависимостьположенияуровняФермиоттемпературыдляGen-типа(а)иp-типапроводимости(б):

а–N_d=10^16см–3;E_d=0,0096эВ;б–N_a=10^16см–3;E_a=0,0104эВ;

учтеназависимостьширинызапрещеннойзоныоттемпературы;навставках

крисункупоказаноповедениеуровняФермивувеличенном масштабе

РассчитатьположениеуровняФермиизуравнениянейтральностииопределитьисходяизположенияуровняФермиконцентрациирав-новесныхэлектроновидырокобычноудаетсятолькочисленнымиме-тодами,заисключениемнесколькихпростыхслучаев.Напрактикевпервуюочередьнеобходимознатьтемпературнуюзависимостькон-центрации.Нарис.6.1вкачествепримераприведеноположениеуров-няФермиизависимостьконцентрацииэлектроновидырокдляGen-иp-типапроводимостиоттемпературы.

Изрисункавидно,чтоуровеньФермипритемпературе,близкойк

0Кдляслучаяоднойдонорнойилиоднойакцепторнойпримеси,ле-

житпосерединемеждууровнемпримесиисоответствующейразре-шеннойзоной.ПомереростатемпературыуровеньФермистремитсякуровнюФерми,всобственномполупроводникеравному



EE^kTlnmn. (6.1.5)

m

2

F i _

p

КогдауровеньФермиE_F

совпадаетсуровнемE_Fi

,концентрации

электроновидырокравныиравнысобственнойконцентрации.Этопроисходиттогда,когдасобственнаяконцентрацияносителейстано-витсябольше,чемконцентрациядонорныхилиакцепторныхприме-

сей,т.е.придостаточновысоких

log(n,p),см^–3

17

16

15

14

13

12

11 _ni

10

9

8

температурах.Температурнаяза-висимостьконцентрацииэлек-

троновдляситуации,показаннойнарис.6.1,а,приведенанарис.6.2.

Каквидноизрисунка,собст-

веннаяконцентрацияэлектроновⁿ экспоненциально убывает суменьшениемтемпературы.На-

клонпрямойзависимости

0 50 100 150 200 250

1000/T

Рис.6.2.Зависимостьсобственнойконцентрацииносителейзарядавгерманиииконцентрацииэлектро-новвзонепроводимостиприN_d=

log_n_if_1000T_равенE_g(0)/2.Назависимостиконцентрацииэлектроноввзонепроводимостиотобратнойтемпературынаблю-

даетсятрихарактерныхучастка:

=10¹⁶

_см–3

оттемпературы

1. привысокихтемпературах

nn_i;

2. принизкихтемпературахnрастетсповышениемтемпературыснаклономE_d/2,чтосоответствуетвсебольшемууходуэлектроновсдонорногоуровня;

3. припромежуточныхтемпературахнаблюдаетсяучасток,гдеnоттемпературыпрактическинезависит.Этосоответствуеттакназы-ваемомуистощениюпримесногоуровня.