6. Цветовоезрение

ИЦВЕТОВОЙТРЕУГОЛЬНИК

Вышеобсуждалисьэнергетическиехарактеристикиизлученияиихвоздействиенаглазчеловекакакприемникизлучения.Приэтомсуще-ственно,чторазныедлиныволнвоздействуютнаглазпо-разному.Вопределенномспектральноминтервалеглазспособенразличатьдлиныволнпоощущениюцвета,которыйформируетсявмозгуподвоздейст-виемтойилиинойдлиныволныизлучения.Другимисловами,человекобладаетцветовымзрением.Нарис.5.14даныназванияцветов,кото-рыесвязанысдлинойволныпадающегоизлучения.Цветовоезрение

можнообъяснитьнаосноветакназываемойтрехцветнойтеориизре-ния,согласнокоторойвглазуимеютсячувствительныеэлементы(кол-бочки)трехвидов,каждыйвидреагируетпреимущественнонаодинизосновныхцветов.Всесуществующиевприродецветаможнополу-чить,смешиваявсоответствующихпропорцияхосновныецвета:крас-

ный(_R700

нм),зеленый(_G546,1нм)исиний(_B435,8нм).

Приэтомникакойосновнойцветнеможетбытьполученврезультате

комбинациидвухдругихцветов.

Длятогочтобыпроводитьцветовыеизмерения,используетсяко-

личественноеописаниецветов[5.5,5.6].ВсистемеRGB(попервойбуквеанглийскихназваний)основныецветаполучилиобозначенияR,GиB.Хотясамасистемавнастоящеевремянеприменяется,рассмот-рениеименноэтойсистемыполезнодлясравнительнопростоговос-приятияпринциповметрологиицвета,иликолориметрии.Вколо-риметрииможноиспользоватькакэнергетические,такисветовыеединицы,нообычноприменяютспециальныеколориметрическиееди-ницы.Выборпроводитсятакимобразом,чтосмешениеосновныхцве-тов,взятыхвравномколичествеэтихединиц,давалобыврезультатебелыйцвет.Изэкспериментаизвестно,чтодляполучениябелогоцветанужносмешатьоднупроизвольнуюединицукрасного,4,59единицзеленогои0,06единицсинегоизлучения.Этиколичествавыбраныкакотносительныеколориметрическиеединицыиназываютсяяркостными

коэффициентами

L_R,L_GиL_B.Применяютсятакжеабсолютныеярко-

стныекоэффициенты,которыеизмеряютсявканделахнаквадратныйметр(кд/м²):

B_R680;

B_G3121;

B_B41.

Количестваосновныхцветовможнотакжевыражатьвединицах

световыхпотоков

F_R,F_G,F_B,которыеизмеряютсявлюменахичис-

ленноравныяркостнымкоэффициентам.

ПереходкэнергетическимхарактеристикамR,G,Bосуществля-

етсяпоправилам,описаннымвыше,такчто

R0,357B_R243,9Вт;G0,00148B_G4,66Вт;B0,0826B_B3,38Вт.

ЦВЕТОВОЕПРОСТРАНСТВО

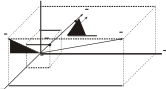
Идеясозданияцветовогопространстваосновананатом,чтоцветможнопредставитькаквектор.Рассмотримпрямоугольнуюсистемукоординатсосями,накоторыхотложеныяркостиосновныхцветов(рис.5.15).

G

g

Б

N

1

Яркость

_Г Ц

М

r _R

Ч ¹

1

b

В

Рис.5.15.СхематическоеизображениевекторацветавRGB-координатах

НачалокоординатобозначаетсябуквойЧ,чтоозначает–черныйцвет.Действительнонулевойвекторимеетнулевыесоставляющиеос-новныхцветови,следовательно,нулевуюяркость.Проведемтеперь

черезточкуМскоординатами(1,1,1)вектор,накоторомрасполагает-сяточкаБ,определяющаяположениебелогоцветавцветовомпро-странстве.КаждаяточкаэтоговектораимеетодинаковыекоординатыповсемосямилинияЧБназываетсяахроматическойосью.Очевид-

но,чточембольшиезначенияимеюткоординатыточки,находящейся

наэтойоси,тембольшеяркостьцветов.Померепродвиженияотточ-

киЧнулевойяркости,выражающейчерныйцвет,яркостьувеличива-ется,иесли,например,точкеМсоответствуеттемно-серыйцвет,тоточке^N–светло-серый,аточкеБ–белый.Изменениеяркостипомерепродвиженияпоахроматическойосиотначалакоординатпока-занострелкойнарисунке.Насыщенностьцветавозрастаетпомереудаленияотахроматическойоси.

Вцветовомпространствевекторкаждогоцветаимеетопределен-

ноенаправление.Рассмотримвкачествепримера,какизображается

^{векторголубогоцвета(векторГнарисунке).Голубойцветполучаетсяаддитивным}сложениемсинегоизеленогоцветабезпримесикрасного,

поэтомунасыщенныйвекторголубогоцветалежитвплоскостиGB.ЕслиэтотвекторотклонитьотплоскостиGBнакакой-тоугол,тоонстанетненасыщенным.ОставаясьвплоскостиGB,ноизменяяугол^{наклонавсторонуосиGилиосиB,вектор,оставаясьголубым,при-}

обрететзеленоватыйилисиневатыйоттенок.

Произвольныйвекторскоординатами(r,g,b),показанныйнари-

сунке,можетбытьописанкак

ЦrRgGbB.

Цветовыеуравнения,какиобычныеалгебраическиеуравнения,аддитивны:еслиимеютсядвавектора,описывающиедвацвета,тосуммарныйвекторимеетцветовыекоординаты,равныеалгебраиче-скойсуммекоординатисходныхвекторов.Втожевремянужнопом-нить,чтоцветовоепространствонеимеетотношениякпространствурасстояний.

ОСОБЫЕПЛОСКОСТИИ ЛИНИИЦВЕТОВОГОПРОСТРАНСТВА

Накоординатныхосяхотложимединичныеотрезки,какэтосдела-нонарис.5.15,новяркостныхколориметрическихединицах,ипроведемчерезточкиB_R1,B_G1,B_B1плоскость(рис.5.16).

G

В_G=1

Т

0

KВ_B=1

В_R=1

^S R

В

U

Рис.5.16.Цветовойтреугольник

Какизвестно,уравнениеплоскости,проходящейчерезтриточкинаконцахотрезковосейкоординат,записываетсяввиде:

r_g

B_R B_G

^b1,

B_B

гдеr,g,b–текущиекоординатыпоосямR,GиBсоответственно.

Таккакпопостроению

B_R1,B_G1,B_B1,то

rgb1.Это

означает,чтосуммацветовыхкоординатвсехточек,лежащихвплос-кости,которойпринадлежитвыделенныйнарисункетреугольник(са-маплоскостьнарисункенеобозначена),равнаединице,асамаплос-

костьестьплоскостьединичныхцветовилиплоскостьцветностей.Треугольник,образованныйпересечениемплоскостицветностейско-ординатнымиосями,называетсятреугольникомцветности,илицветовымтреугольником.Таккакмодульцветалюбойточкинаплоскостицветностейравенединице(rgb1),тоцветанаэтой

плоскостиимеютодинаковуюяркостьвколориметрическихединицах,норазныеприизмеренияхвканделахнаквадратныйметр.Еслинарис.5.16провестиплоскостьчерезточкиS,TиUнаосяхR,GиB

скоординатами1B_R,0,02B_G

и17B_B

соответственно,тообразован-

наяплоскостьназываетсяплоскостьюравныхяркостей,каждаяточ-какоторойотноситсякцвету,яркость которогосоставляет680кд/м².Вцветовомпространственаходитсямножествоплоскостейравныхярко-стей,втомчислеиплоскостьснулевойяркостью,проходящаячерезначалокоординат.Всеплоскостиравныхяркостейпараллельныдругдругу.Линияпересеченияплоскостиединичныхцветовиплоскостиравныхяркостей(линияSKнарис.5.16)называетсялиниейравнойяркости.

СВОЙСТВАЦВЕТОВОГОТРЕУГОЛЬНИКА

Плоскостьцветовоготреугольникаприменяютдляописанияцвет-ности,непользуясьтрехмернымисхемами.Дляэтогоотсчеткоорди-натведетсятак,какпоказанонарис.5.17.

Координатыкаждойосиотсчитываютсяпонаправлениюксоответ-ствующейвершинецветовоготреугольника.Длятогочтобыопреде-литькоординаты,например,точкиЦ,единичныйцветкоторойдается

уравнением:

^Цr_Ц^Rg_Ц^Gb_Ц^,

G

^g0,6

g

0,8

0,2

0,4^r

r_Ц

0,2

Ц

0,4

_Ц 0,6Б

0,8

b_Ц

^В 0,8 0,6 0,4 0,2 ^R

b

Рис.5.17.Отсчеткоординатиопределениекоординатцветности

необходимопровестипрямые,параллельныесторонамцветовоготре-угольника,какэтопоказанонарисунке.Аналогичноможнонанеститочкулюбогоединичногоцвета,знаяеекоординаты.Вообщеговоря,положениелюбойточкивтреугольникецветностиопределяетсятоль-кодвумякоординатами–этоследуетизтого,чтосуммакоординатцветностиравнаединице.Ахроматическаяосьпересекаетплоскость

цветовоготреугольникавточкеБ,котораяотображаетбелыйцветиуравнениецветностидлякоторойимеетвид:

Б^1R^1G^1B.

3 3 3

СудалениемточкиотахроматическойосиеенасыщенностьрастетпопрямойотнулявточкеБдомаксимальногозначениявточкенаоднойизсторонтреугольника.Уравнениецветностизаписановпред-

положении,чтоосновныецветавыраженывколориметрическихеди-

ницах.Еслионивыраженывстандартныхсветовыхединицах,токо-

ординатыбелойточкиравны0,177;0,813и0,001ирасполагатьсяонанебудетневцентретреугольника,авблизивершиныG(рис.5.17).Еслижеосновныецветавыраженывэнергетическихединицах,тобелаяточкаоказываетсяблизкорасположеннойкR–вершинецве-товоготреугольника.Впервомслучаеточностьопределениязеленого

иблизкихкнемуцветов,авовтором–красногоиблизкихкнему

y

0,8

0,7

0,6

0,5

0,4

0,3

100

510

500

490

520

90

530

80

70

540

60

50

40

30

20

10

550

560

570

580

590

600

610₆₂₀

630

648

0,2

0,1

480

470

460

450

440430

540΄

530΄

520΄

510΄

500΄

700

0 0,1

^4000,2 0,3 0,4 0,5 0,6 0,7 x

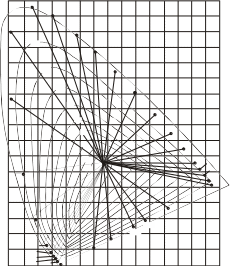
Рис.5.18.ЦветовойграфиквМеждународнойколориметрическойсистемеXYZ:

вцентре–точкабелогоцвета,отнееотходятпрямые,соединяющиебелыйцветсоспектральнымицветами,цифрамипопериметрупоказаныдлиныволн;кривыелиниивокругбелогоцветасоответствуютодинаковойчисто-тецвета10,20,…100%(100%соответствуетчистымспектральнымцве-там).Внижнейчастиграфикавдольлиниичистыхпурпурныхцветовцифрамисоштрихамиотмеченыдлиныволн,дополнительныексоответ-

ствующимпурпурнымцветам

цветовснижается,иименновэтомсостоитпричинатого,чтоисполь-зуетсяколориметрическаясистемаединиц.

Мырассмотрелипринципыиидеи,заложенныевосновупредстав-ленийоцветовомпространствеицветовомтреугольнике.НапрактикетрехкоординатнаясистемацветностиRGBнеиспользуется,аисполь-

зуетсяинаясистемаXYZ,основаннаянатрехосновныхцветах,болеенасыщенных,чемспектральные,т.е.наотсутствующихвприроде.Ос-новныецветасистемыXYZзаписываютсявсистеме^{RGBследую-}

щимобразом:

X0,4185R0,0912RG0,0009B;Y0,1588R0,2524G0,0025B;Z0,0829R0,0157G0,1786B.

ЦветXблизокккрасномуцветуR,нонасыщеннееего(имеетсяоднаотрицательнаякоордината),цветYсущественнонасыщеннеезеленого^{G(имеется}двеотрицательныхкоординаты),цветZголубееBиболеенасыщен.Переходотоднойсистемыкдругойосуществля-

етсяприпомощипростыхформулпреобразованиякоординат,извест-

ныхизаналитическойгеометрии.КакидлясистемыRGB,длясисте-мыXYZнезависимымиявляютсятолькодвекоординатыцветности.ВколориметрическойсистемеXYZпринятцветовойграфик,который

получается,есливпрямоугольнойсистемекоординатиспользуются

осиYпоабсциссеиZ–поординате.

Нарис.5.18приведенцветовойграфик,принятыйвМеждународ-нойколориметрическойсистеме,используемыйдляцветовыхрасче-тов.Вцентральнойчастирисункарасположенбелыйцвет,авдольли-нийспектральныхцветовотложеныдлиныволн,соответствующиеотдельнымспектральнымцветам,измеренныевнанометрах.Напря-мыхлиниях,соединяющихцентррисункаслиниямиспектральныхцветов,располагаютсяцвета,полученныесмешением.

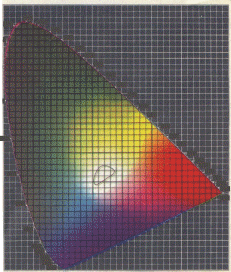
Нарис.5.19цветовойграфикпоказаннепосредственновцвете,такчтовидно,вкакомсоответствиинаходятсяцветаикоординатыграфика.

0,9

y

0,8

510

0,7

505

0,6

500

0,5

515

520₅₂₅

530

535

540

545

550

555

560

565

570

575

580

0,4

0,3

0,2

495

490

485

585

590

595

600

605

610

620

630

650

700

0,1

480

475

470

465

460

450

0 0,1 0,2 0,3 0,4 0,5 0,6 0,7

Рис.5.19.ЦветовойграфиквМеждународнойколориметрическойсистеме