1. Решениенаосновеэлектростатическойаналогии

Аналогиямеждуэлектрическимиитермическимивеличинамипо-зволяетпостроитьэффективныйрасчетныйметодопределениянеста-ционарныхтемператур.Еслидеталираспределениятемпературывнут-риэлементатермическогосенсоранесущественны(например,из-замалостиегоразмеров),тоизменениетемпературыопределяетсяурав-нениемтепловогобалансавупрощеннойформе:

dT

^{C ФGTT}_0^{, (1.9.1)}

dt

где^C–теплоемкостьэлемента;Ф–мощностьвнутреннихисточни-ков(илистоков)тепла;G–термическаяпроводимость,учитывающая

теплообменсокружающейсредой;TиT₀

окружающейсреды.

–температураэлементаи

Есливпроцессетеплообменатемператураокружающейсредынеменяется,тоееможновзятьвкачествеопорной,T_0const.

^{Интегрированиеуравнения(1.9.1)сначальнымусловием:u0}^0

приводитквыражению

^  ^

u^Ф_1exp_^t_, (1.9.2)

^{G }

^

где

uTT_0–перегревсенсораотносительноокружающейсреды;

^C

G

–постояннаявременитепловогосенсора,равнаявремени,зако-

тороеперегревдостигает63%стацио- ^T

нарногозначенияu_t_Ф/G.

Эквивалентнаяэлектрическаясхе- _{Ф С} ^G

ма, соответствующая рассматривае-

мой,тепловойзадачеиуравнению

(1.9.1),приведенанарис.1.27.Техника

0

^{расчетапереходныхпроцессоввэлек-} T

трическихцепяхразвитаоченьхоро-

шо,чтопозволяетизвестныерезульта-тыдляэлектрическихцепейперенестинаэлементытермическихсенсоров.

Рис.1.27.Эквивалентнаяэлект-

рическаясхемасоответствую-щаязадаче(1.9.1)

Вчастности,есливыделяющаясятепловаяэнергияизменяетсяпогар-

моническомузаконуФФ₀e^it,где–частотаизменений,топере-гревопределяетсячерезимпедансэлектрическойцепиz,приведен-ныйнарис.1.27:

где

z ¹ и

GjC

uzФ, (1.9.3)

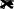j1;GиC–соответственнотермическая

проводимостьитеплоемкость.

Температурныйперегревоказываетсясдвинутпофазеотноситель-ноисточникатепловойэнергииФ:tg^C.

G

Еслиусловиепостоянстватемпературывдольтермосенсораявля-

етсяслишкомгрубым,топрименяютмоделисраспределеннымипа-раметрами.Вкачествепримерарассмотримслучайодномерноготеп-ловогопотокачерезбалочкупостоянногосечения.Впределахпоперечногосечениятемпературапредполагаетсяпостоянной.

РазобьемдлинубалочкинаNодинаковыхэлементовx.Каждый

элементбудемхарактеризоватьтемпературойоднойеготочки(илиузла),связанной,например,ссерединойотрезка.Уравнениетепловогобалансадляi-гоучасткатермосенсоразапишемввиде:

С^x^Ti^{Ti1Ti}^{TiTi1}GxTФx. (1.9.4)

t Rx Rx ⁱ

ЗдесьC^СS^–теплоемкостьединицыдлиныбалочки,Дж/(мК);R(kS)^1–тепловоесопротивлениеединицыдлиныбалочки,К/(Втм);G–тепловаяпроводимостьсповерхностибалочкинаеди-^{ницуеедлины,Вт/(м}К)^{;Ф–мощностьвнутреннихтепловыхисточ-ников}(стоков)наединицудлины,Вт/м.

Двапервыхчленавправойчастиуравнения(1.9.4)описываютиз-

менениетепловойэнергииi-гоэлементаврезультатетеплообменас

соседнимиэлементами,третий–тепловыепотерисповерхностиэле-мента,четвертый–действиевнутреннихисточниковтепла.

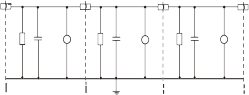
Нарис.1.28приведенаэквивалентнаяэлектрическаясхемачастибалочкиввиделиниисраспределеннымипараметрами.

1

_2RΔX

^ΔXi–1

1

_2RΔX

1

_2RΔX

ΔX_i

1

_2RΔX

1

_2RΔX

^ΔXi+1

1

_2RΔX

GΔX

GΔX

1

ФΔX

GΔX

GΔX

1

ФΔX

GΔX

GΔX

1

ФΔX

Рис.1.28.Эквивалентнаяэлектрическаясхемадлятемпературногополяпря-моугольнойбалочки

Длянахожденияраспределениятемпературыивеличинтепловыхпотоковнеобходимозадатьграничныеусловиянаконцахлинии.ЧащевсегоониформулируютсязаданиемлиботемпературыT_xLT_0,либо

величинытепловогопотока

T

^xxL

RФ,гдесимволомLобозначен

соответствующийкрайлинии.Вэквивалентнойэлектрическойсхемекеекраямприсоединяетсясоответственноисточникнапряженийилитока.

Последовательностьрасчетовприиспользованиимоделидлиннойлиниисводитсякследующему.Термическийсигнал,изменяющийсявовремени,разлагаетсяврядФурье.Далеерассматриваетсявоздействиеналиниютолькогармоническогосигналавыбраннойчастоты.Реше-ниетакойзадачиописановмногочисленныхучебниках,например,в[1.26–1.28],ипозволяетнайтираспределениетемпературитепловыхпотоков.Суммированиемчастныхрешенийпоспектручастотрас-сматриваемоготермическогосигналанаходитсяобщеерешение.