2. Точечныйисточниктепла

Иноераспределениетемпературынаблюдается,еслитепловыделя-етсямалогабаритнымрезистором,встроеннымвдиафрагму.Дляуп-рощениярасчетовбудемсчитать,чторезисторимееткольцевуюфор-

мурадиуса

рис.1.24,б).

r_i,причемr_i

R_i,ирасположенвцентредиафрагмы(см.

Какивпервомслучае(рис.1.24,а),теплораспространяетсяпо

диафрагме,одновременнорассеиваясьвокружающеепространство.

Малостьразмеровобласти,занятойрезистором,позволяетупро-ститьформулировкукраевойзадачи.Во-первых,набольшойчасти

диафрагмытепловыделениянет,чтоприводитдифференциальноеуравнение(1.8.1)квиду

^1dr^duu0. (1.8.9)

rdr^

dr^

 

Во-вторых,можнопренебречьтеплопотерямивобластирезистора.Граничныеусловиясучетомэтогоможносформулироватьввиде

du _ Ф

; (1.8.10)

^drrr_i

h2r_ik

^uR^0.

Первоеграничноеусловиев(1.8.10)означает,чтовседжоулевоте-

пло

ФI^{2R,выделяющеесянарезисторе,уходитвдиафрагмучерез}

поверхностьцилиндрическогосечения

диафрагмы.

S2r_ih,гдеh–толщина

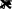
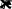Общеерешениеуравнения(1.8.9)имеетследующийвид:

^ur^c₁^I_0^r

_c_2K0r

_,

(1.8.11)

r_1rR.

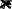
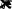Граничныеусловия(1.8.10)приводяткуравнениямнакоэффици-ентыc_1иc_2:

^uR^c₁^I_0^R

_c_2K0R

_0;

^du cI

i

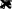
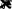 cK

r  ^Ф

(1.8.12)

11

^drrr_i

21 i

.

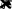
2r_ihk

Впоследнемуравненииучтеныдифференциальныесвойствамо-дифицированныхфункцийБесселя[1.24]:

dI

^0I_1^x^;

^0K_1^x^.

dK

dx dx

Решениесистемыуравнений(1.8.12)позволяетзаписатьраспреде-лениетемпературыподиафрагмевследующемвиде:

K_r

_K_R

I_r_

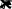
_{}0

0 0

^ur^{ Ф}

I_0R

_

. (1.8.13)

kh2r_i

I_r _

   11

KrK R

0

^{1 0} I_R_

u,К

4,0

3,5

3,0

2,5

2,0

1,5

1,0

0,5

0,0

x

0,0 0,2 0,4 0,6 0,8 1,0^R

Рис.1.26.Радиальноераспределениетемпературыдлякруглоймембраныс«точечным»источникомтепла:

радиуспластиныR=2,5мм,толщинаh=20мкм;коэффициенттеплопроводностикремнияk=96Вт/(м∙К);радиусразогреваемойцентральнойобластиr_i=0,01R;тепловойпотокФ=0,01Вт

МножительпередтепловымпотокомФпредставляеттепловоесо-противлениекруглойдиафрагмыдлярассматриваемойгеометрии.Со-отношением(1.8.13)удобнопользоватьсядлякалибровкитермопаритерморезисторов,входящихвсоставтермическихсенсоров,имеющихплоскуюкруглуюдиафрагму.Радиальноераспределениетемпературывсоответствиис(1.8.13)представленонарис.1.26.Численныеданныедлярасчетауказанывподписикрисунку.

9. Температурнаядинамикаэлементовтермическихсенсоров

Оченьчастотермическиесенсорыработаютвдинамическомре-жиме,когдатепловыепотокиитемпературавразличныхчастяхсен-соразависятнетолькооткоординат,ноиотвремени.Вэтомслучаезадачаобопределениитемпературныхполейсущественноусложняет-сяиеерешение,какправило,проводитсячисленнымиметодами

сприменениемспециализированныхпакетовпрограмм,например,ANSYS[1.25].

Вданномпараграфевпервойчастибудетрассмотренпрактически

важныйметод,использующийаналогиюмеждуэлектрическимиитер-мическимивеличинами,ужеописаннуювпараграфе1.6.

Вовторойчастипараграфатемпературнаядинамикарассматрива-етсяврамкахстандартногоаналитическогометодарешениянаприме-ретермическогосенсорабалочноготипа.