6. Стационарноетемпературноеполевкруглойдиафрагме

Введение

Диафрагмыразличныхформчастоприменяютсявкачествеэле-ментовтемпературныхсенсоров.Приэтомтолщинадиафрагмможетбытьпостояннойлибопеременной,например,сутолщениемвцентре,асоединениескольцомжесткостиможетосуществлятьсяповсейгра-ницелибопоеечасти(рис.1.23).

Поддерживающиеполоски

Кольцо

«Плавающая»диафрагма

Рис.1.23.Диафрагмастепловымконтактомпочастиграницы

Различныеконструкционныерешенияпризваныобеспечитьполу-чениемаксимальныхтемпературныхперепадовмеждуцентромдиа-фрагмыикольцомжесткостиприсохранениивысокойстойкостикмеханическимвоздействиям.

Уплоскойкруглойдиафрагмы(рис.1.24)механическиехарактери-стикизначительнолучше,чемудиафрагмынарис.1.23ссоедини-тельнымиполосками,осуществляющимимеханическийитепловойконтакт.Повеличинежетепловогосопротивлениямеждуцентромдиафрагмыикольцомжесткостисоотношениеплавающейиплоскойдиафрагмоказываетсяобратным.Поэтомуприконструированиитер-мическихсенсоровприходитсянаходитькомпромиссмеждутепловы-мииконструктивнымитребованиями.

Границадиафрагмы

^{r d}r

^rкольца

Нагреваемаядиафрагма

а

r ^dr

^ri ^{rкольца}

Нагреватель

б

Рис.1.24.Диафрагмастепловымконтактомповсейгранице

Рассмотримсначалараспределениетемпературывплоскойкруг-лойдиафрагме,наверхнююповерхностькоторойприходиттепловой

потокпостояннойплотностиq₀

(см.рис.1.24,а).Далеенайдемрас-

пределениетемпературыдляслучаяточечногоисточникатепла,рас-положенноговцентрепластины(резистивныйнагрев)(рис.1.24,б).

1. Однородныйнагрев

Предположим,какэтообычнореализуетсянапрактике,чтотемпе-ратуранаграницесоединениядиафрагмыикольцажесткостиподдер-

живаетсяпостоянной

(TT₀₎

иперегревотсутствует

_uR0_.

Из-засимметриидиафрагмыиграничныхусловийперегревзависиттолькоотрасстояниядоцентраr.ТогдастационарноераспределениетемпературыопределяетсяуравнениемПуассона,котороевполярнойсистемекоординатимеетследующуюформу:

^1dr^duu, (1.8.1)

rdr^

dr^

где

^

hk

 

;–коэффициенттеплообмена

^q0

kh

(остальныеобо-

значения–каквпараграфе1.7).

Праваячастьуравнения(1.8.1)учитываетразогревиз-запоглоще-нияизлучения,второеслагаемоевлевойчасти–теплообмендиафраг-мысокружающейсредойпозаконуНьютона.

Граничныеусловияврассматриваемойзадачеимеютвид

u_rR0;

du

^drr0

0.

(1.8.2)

Последнееусловиеследуетизсимметриизадачи,котораяприводиткмаксимальномуперегревувцентрепластины.

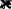Введяновуюпеременнуюx_1r

вуравнение(1.8.1),получаем

d²u

1du 



dx^{2 }

u . (1.8.3)

dx 

₁ 1 1

Однородноеуравнение,соответствующее(1.8.3),

d²u

1du



dx^{2 }

–u0

dx

(1.8.4)

₁ 1 1

являетсячастнымслучаемуравнениянамодифицированныефункцииБесселяпорядкануль[1.24].Егообщеерешениеимеетвид:

^uc₁^I_0^x_1^c₂^K_0^x_1^{, (1.8.5)}

где

I_0x_1–модифицированнаяфункцияБесселянулевогопорядка;

K_0x_1–модифицированнаяфукцияБесселявторогороданулевогопорядка(функцияМакдональдса).

Каждаяизэтихфункцийможетбытьпредставленаввидеразложе-

нияврядпопеременной

x_1[1.24]:

_ 2n



I_0

^1x_1

_2  ^;

 ^x

^n0n!

_ 

^2

^{1}^{x2nn1}

(1.8.6)

^k₀^I_0^x_1^ln

^1C__^

^{1 }

_^,

 ² 

^n0_^n!^22 ^l1l_

гдеC0,577216

–постояннаяЭйлера.

Используя(1.8.6),общеерешениенеоднородногоуравнения(1.8.3)можнозаписатьввиде

u,К0,08

0,07

0,06

0,05

0,04

0,03

0,02

^uc₁^I_0^x_1^c₂^K_0^x_1^





. (1.8.7)

0,01

x

^0,00 R

0,0 0,2 0,4 0,6 0,8 1,0

Рис.1.25.Распределениетемпературыпокруглойплоскойдиафрагме:

q₀₌const

повсейповерхности;радиуспластиныR=2,5мм,

толщинаh=20мкм;коэффициенттеплопроводностикремния

k=96Вт/(м∙К);плотностьтепловогопотока^q=100Вт/м²

0

Постоянные

c_1иc₂

определяютсяисходяизграничныхусловий

(1.7.2).Врассматриваемомслучае:

.



c_20;

c_1

I_R _

₀ 

Этоприводиткрадиальномураспределениютемпературыдиа-фрагмыпозакону:

_^ I_0r

_

 



0^

^ur^{ 1}

^ I R



. (1.8.8)

_



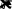
Температурадиафрагмымонотонноуменьшаетсяотцентраккраю(рис.1.25).

Увеличениеразмеровдиафрагмыприводитквозрастаниютемпера-

турывеецентре.Изсоотношения(1.8.8)следует,чтомаксимальныйперегревплоскойдиафрагмывслучаеравномерногонагревасоставляет:

_ 

u(0)

^1

_

1

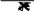I_0R

_.

_

 