1. Тепловоесопротивлениесоставнойтеплопроводящейпла-стины.

Найдемтепловоесопротивлениепластины,состоящейиздвухсло-

ев,имеющихразличнуютеплопроводность(рис.1.18).

Наэтомжерисункеприведенаэквивалентнаясхемасоединениятепловыхсопротивленийотдельныхслоев,справедливаяприусловии,чтонаграницеразделаслоевнетдополнительныхисточниковилисто-

ковтепла.Вэтомслучаеобщеетепловоесопротивлениепластиныбу-детравно

R^1l1

^1l2, (1.6.6)

k_1A k_2A

где

k₁,l_1и

k_2,l_2–коэффициентытеплопроводностиитолщинысоот-

ветствующихслоев;A–площадьпластины.

T₁ T₂

_n–

T₁ T₂

^–_q q

R₁

l l

R_T1 R_{T2 R2}

Рис.1.18.Красчетутепловогосопротивлениядвухслойнойпластины,когдаqn,n–

нормалькповерхностираздела

пластин

Рис.1.19.Красчетутепловогосопротивлениясоставнойпла-

стины

Обобщаяформулу(1.6.6)натотслучай,когдапластинысостоятиз

n-слоев,получаемформулу(1.5.4).

2. Параллельное соединение двух разнородных тепловых

структур.

Нарис.1.19представленасоставнаяпластина,образованнаяпарал-

лельнымсоединениемдвухразнородныхпотеплопроводностимате-риалов.Длинаишириначастейпластиныпредполагаютсяодинаковы-ми.Здесьжеприведенаэквивалентнаяэлектрическаясхема,общеесопротивлениекоторойравно

R^R1R2.

R_1R₂

Учитываяаналогиитабл.1.2,дляобщеготепловогосопротивлениясоставнойпластиныполучаем:

1L1 L

_Rk_1l1wk_2wl2

, (1.6.7)

^T 1L 1L



k_1l1w k_2l2w

гдеl,w,L–толщина,ширинаидлинасоответствующегослоя.Общаятепловаяпроводимостьnпараллельносоединенныхслоевравнасум-метепловыхпроводимостейотдельныхструктур

n

G_

i1

k_il_iwL

. (1.6.8)

6. Температурноеполевинтегральнойконсольнойбалочке

Тонкаяпрямоугольнаякремниеваябалочка,сформированнаясприменениемглубокогоанизотропноготравленияистандартныхме-тодовмикроэлектроннойтехнологии(рис.1.20),входитвсоставрядатепловыхсенсоров,которыеприменяютсядляизмерениядавленияга-за[1.21],потокаинфракрасногоизлучения[1.22]илиэнергииэлектро-магнитногоизлучениярадиочастотногодиапазона[1.23].Пятьсторонтакойбалочкисвободны,авдольшестойсоздаетсятепловойимехани-ческийконтактскольцомжесткости.Наповерхностибалочкиобычно

формируютсятермопарыилитерморезисторы.Тепловойпоток(на-пример,ИК-излучения)поглощаетсяприемнойплощадкойlидалеераспространяетсяккольцужесткости.Изменяягеометрическиеразме-ры,можноуправлятьтепловымсопротивлениембалочкивширокихпределах,такчтомеждуприемнойплощадкойикольцомжесткостивозникаетразностьтемператур,котораярегистрируетсятермоэлемен-тами.Широкоекольцожесткостипредставляетсобойтепловуюзако-ротку,из-зачеготемпературавдольсторонызакреплениябалочкиока-зываетсяпрактическиравнатемпературеоснованиякольцажесткости.

Зонавзаимодействия Термопара

Кольцо

W

D

l L

Рис.1.20.Термическийсенсорсконсольнойбалочкой

Еслибалочканаходитсяввакууме,топереностеплаопределяетсямеханизмомтеплопроводностиеематериала.Перегревприемнойпло-щадкиотносительнокольцажесткостиобычнонепревышаетнесколь-кихградусов,поэтомурадиационныммеханизмомтеплопотерьможнопренебречь.

Вэтихусловияхраспределениетемпературымеждукраемприем-нойплощадкиизащемлениемлинейнопокоординате,атепловоесо-противлениеучасткабалочкидлинойLописываетсяпростейшимсо-отношением(1.2.15).

Обычно,однако,балочканаходитсявгазовойсреде,когда,помимо

теплопроводностикремния,необходимоучитыватьтеплопотери,вы-званныетеплопроводностьюгазаиконвекцией.Вэтомслучаераспре-делениетемпературывдольбалочкиописываетсянелинейнойзависи-мостью.Рассмотримэтотслучайподробнее.Нарис.1.21приведенагеометриярассматриваемойзадачи.

ПотокИК-излученияплотностьюq₀

падаетнаприемнуюплощад-

кудлиной^l,покрытуюсоднойсторонычернымпокрытием,такчтовсеизлучениеполностьюпоглощается.

0

_z q _y

h

_W x

l _L

Рис.1.21.Красчетутемпературногополябалочки

Размерыбалочкивнаправленииzпредполагаютсямалыми,такчтотемпературувпределахсеченияможносчитатьодинаковой.Этоусловиехорошовыполняетсядлякремния,обладающеговысокойтеп-лопроводностью.Поглощаемоеизлучениеэквивалентнодействиюобъемнораспределенныхисточниковтепласплотностью

f^dQ^q0dA^q0, (1.7.1)

dV hdA h

гдеdVhdA–элементобъемабалочкитолщинойhисбоковойпо-

верхностьюdA;научасткеdA.

dQq_0dA–количествоИК-излучения,поглощенное

Количествотепла,теряемоезаединицувременисповерхностиdA,

определяетсязакономНьютона(1.4.4):

dQuPdx, (1.7.2)

где–коэффициенттеплообмена;

uTT_0–температурныйпере-

гревбалочкиотносительноокружающейсреды,имеющейтемпературу

T_0;P2w2h–периметрсечениябалочки.

Сучетомравенства(1.7.1)и(1.7.2)уравнениетеплопроводностипринимаетвид:

u ²u ^q P

^{c k 0 u,} (1.7.3)

t _x² h S

где^Swh

–сечениебалочкииучтено,чтотеплораспространяется

тольковдольдлиннойосибалочки^x.

Рассмотримдалееслучайстационарноготепловогопотока,когдараспределениетемпературынезависитотвременииуравнение(1.7.3)принимаетособеннопростуюформу:

2

a^2duuf, (1.7.4)

dx²

гдеa^2k;^P;

f^q0.

S h

Коэффициенттеплообменаможетбытьразличнымнаприемной

площадкеинаостальнойчастибалочки,_1_2.Сучетомэтогокрае-ваязадачанастационарноераспределениетемпературывбалочкеформулируетсяследующимобразом.

1. Область1,0xl.

2

a^2du1u

f; (1.7.5)

du₁

dx²

0;

11

1

^1P. (1.7.6)

dx_x0 S

Граничноеусловие(1.7.6)отражаеттеплоизолированностьсвобод-ногоконцабалочки.

2. Область2,lxL.

2

2

a^2du2udx₂

0; (1.7.7)

^u2xL^0;

2

^2

^P. (1.7.8)

S

ПерегревнакраюбалочкиприxL

отсутствует.Награницеоб-

ластей1и2выполняютсяграничныеусловияравенстватемпературыитепловыхпотоков:

^u1xl^u2xl^;

_kdu1

^dxxl

_kdu2

dx

.

xl

(1.7.9)

Решениекраевойзадачи(1.7.5)...(1.7.9)имеетследующийвид:



u^f_1

^k₂^ch(k_2^{Ll)ch(k}₁^{x) }_;

¹ kch(k

^Ll)ch(kl)

ksh(k

^{Ll)sh(kl)}

^1 ^{2 2  11 2  1}

_uf ^k₁^sh(k₁^l)sh(k_2^Lx) _.

(1.7.10)

² k

ch(k

^{Ll)ch(kl)ksh(k}

^{Ll)sh(kl)}

12 2 1 1 2 1

 

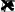
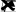
^Здесьk_1

^1, k_2 ^2.

a a

Распределениетемпературывдольдлиннойосибалочкипоказанонарис.1.22,максимальныйперегревнаблюдаетсянаеесвободном

краюпри

x0:

f^{ }



k

_1_



^u_1⁰^

1_ch (k₁l)

^1th(k_2^{Ll)sh(k}₁^l)_ ^.

^_{1 } ^k_{2 }

 

Величинаперегревазависитотразмеровбалочкиикоэффициентовтеплопроводностиитеплообмена.Длябалочкисдлиннойприемной

площадкой,когда

k₁l

1,вторымслагаемымвквадратныхскобках

можнопренебречьиперегревдостигаетпредельногозначения

f

^u_1⁰^{ .}

₁

u,К0,05

0,04

0,03

0,02

0,01

0,00 ^x

0,0 0,2 0,4 0,6 0,8 1,0^L

Рис.1.22.Распределениетемпературыпопрямоугольнойбалочке

Приформулировкекраевыхусловий(1.7.6)и(1.7.8)теплообменомсторцабалочкипренебрегли.Этоможносделать,посколькувреаль-

ныхэлементахмикросистемплощадьторцабалочки

S₁^{многоменьше}

суммарнойплощадиостальныхсторонS,S₁

S.Иногдадляболее

корректногоучетатеплообменасторца(присохранении,однако,гра-ничногоусловия(1.7.6))условноувеличиваютплощадьбоковойпо-^{верхностибалочкиАнавеличинуповерхноститорца.Тогдадлинабалочки}станетравнойL^,величинакоторойопределяетсяочевидным

соотношением

L^PSS_1.Этоприводиткнекоторомуувеличению

размеровприемнойплощадки.