4. Вынужденнаяконвекциядляплоскойповерхности

Вкачествепервогопримера,иллюстрирующегокритериальныйподходкрасчетуконвективноготеплообмена,рассмотримпрактиче-скиважныйслучайобтеканияламинарнымпотокомжидкостиплоскойповерхности,представляющейоднусторонупластины.Пластинапод-держиваетсяпритемпературеT_c,вдалиотповерхностипластиныско-

ростьпотокаитемпературажидкостисоответственноравныu₀

иT_0.

РежимтеченияжидкостиопределяетсякритериемРейнольдса:

ux

Re_x_,причемвкачествехарактеристическогоразмерадляданного

случаяцелесообразновыбратьрасстояниеоткраяпластины–x.ПриэтомчислоРейнольдсазависитоткоординаты,асамкритерийноситлокальныйхарактер,чтоподчеркиваетсяиндексомx.Эксперимен-тальноеисследованиепозволилоустановитьсвязьмеждурежимомте-ченияжидкостиичисломРейнольдса:

ламинарныйрежим:Re_x510^5;переходныйрежим:510^5Re_x310^6;турбулентныйрежим:310^6Re_x.

Теоретическийанализпоказывает,чтотолщинагидродинамиче-

скогопограничногослоя_г

соотношением[1.14]:

зависитоткоординатывсоответствиис

^4,64x. (1.4.24)

x

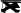^г Re

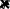ПосколькусамочислоРейнольдсазависитотx,товитогетолщи-

наслояпропорциональна

_г~ x.Этатолщинасравнительноневели-

ка,например,длявоздухапри

u_03

м/с,

t_020C

_г 10,4ммдля

x1м.Нарис.1.12приведеныпрофилигидродинамическогоитерми-ческогопограничныхслоев.

Вгидродинамическомпограничномслоетеплопередаетсяблаго-

дарятеплопроводности.Черезпервыйнеподвижный(из-заадгезион-ноговзаимодействияспластиной)слойжидкоститеплотапередается,

Поток

Гидродинамическийитермический

пограничныеслои

x

Поток

L

а

Гидродинамическийслой

Термическийслой

Nu(L₀)

Nu(0)

1,0

0,8

0,6

0,4

0,2

^L₀ L

0,0

0 2 4 6 8 10

^{(холодный)} x

(нагретый)

L_0/L

б_б в^в

Рис.1.12.Гидродинамическийитермическийслоидляламинарногопото-кажидкостиприоднороднойтемпературе(а)иприналичиихолодногокрая(б),зависимостьлокальногокритерияНуссельтаоткоординаты(в)

каквтвердомтеле.Далеемикрочастицыжидкости,переходявовторойслой,переносятнекотороеколичествотепла_T_cT_0,частькоторого

уноситсядвижущейсяжидкостью(здесьуже

u0),ачастьуходитв

третийслойит.д.Витоге,нарасстоянии_т

отповерхностиокажется

слойжидкости,вкоторыйтеплотанепоступила.Этапристеночная

область,гдетемператураменяетсяотT_c

скийпограничныйслой_т.

доT_0,представляеттермиче-

Расчетыпоказывают[1.17],чтотолщиныгидродинамическогоитермическогослоевсвязанысоотношением:

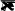^1. (1.4.25)

т _3Prг

ДлявоздухачислоПрандтляPr 0,7,поэтому

_т0,89_г.Вода

притемпературах

t_0100C

такжеимеетсравнимыетолщиныобоих

слоев,адлямасла_т

_г.

Знаниетолщиныпограничногослояпозволяетопределитькоэф-фициенттеплообменаиплотностьтепловогопотока.Длявынуж-деннойконвекциивыражение(1.4.5),определяющееисправедливоедляестественнойконвекции,должнобытьдополненочисленнымко-эффициентом,учитывающимдвижениежидкостивпограничном

слое:

Расчетыдают

^. (1.4.26)

_т

1,5.Ввидупрактическойважностивынужденной

конвекциидляпроектированиямикросистемэтотслучайдалеерас-смотримподробнее.

Учитываявыражения(1.4.24)...(1.4.26),получаемуравнениедля

локальногокритерияНуссельтаивходящеговнегокоэффициентатеп-лообмена:

гдеNu_x

x_.

k

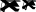Nu_x0,33Re_x

^3Pr, (1.4.27)

Всепараметры,входящиевуравнение,выбираютсяпритемпера-^{туренабегающегопотокаT}₀^.

ПлотностьтепловогопотокаопределяетсязакономНьютона.

Изсоотношений(1.4.24)и(1.4.27)вытекает,чтосувеличениемрасстоянияxотпереднейкромкипластиныкоэффициенттеплообмена

уменьшается,

^1.Этоявляетсяследствиемвязкостижидкостии

x

возрастаниятолщиныпограничныхслоевпомереувеличенияx.Зави-симостьоткоординатлокальногокоэффициентаисвязанныхснимкритериевдляпрактическихрасчетовнеудобна,поэтомуобычноис-пользуютихусредненныезначения.

Так,длясреднегокоэффициентатеплообменаучасткапластины

А

длинойL,учитывая,что

_x ,гдеА–коэффициент,независя-

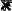x

щийоткоординат,из(1.4.27)получаем:

L

¹_

L₀

_xdx2

^А. (1.4.28)

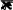L

СреднийкоэффициенттеплообменаучасткапластиныдлинойLоказываетсявдвоебольше,чемлокальныйкоэффициентприxL.По-этомуиз(1.4.27)дляусредненного числаНуссельтаполучаем

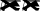Nu0,66Re_L^3Pr_L.

Большойпрактическийинтереспредставляетслучайобтеканияплоскойповерхностипластины,укоторойнагретыйучастокстемпе-

ратуройT_c

начинаетсянанекоторомрасстоянииxL

отеепередней

кромки(рис.1.12),аобласть0xL

имееттемпературунабегающе-

гопотока.Приламинарномобтеканиитакойпластинылокальноечис-

лоНуссельтадляL_0xL

оказываетсяравно[1.14](рис.1.12,в):

_{  }3

0

 

0,33



0,33^uL0,5^xL^0,5

^{xL 4}

^Nu_x^0,33^Pr

^{ } 

_{ }1_

0 0_{ }

. (1.4.29)

^  ^L 

_  ^L0  _

 

СреднеезначениекритерияНуссельтаNuиз(1.4.29)находится

численнымиметодами.При

^L4

L₀

расчетнаязависимостьсточно-

стью2%аппроксимируетсявыражением[1.7]:

1

^NuL_0

^Nu0

0,825^L2.

 

^L0

Приведенныевышеоценкикоэффициентатеплообменаотносятсякламинарномурежимутеченияжидкости.Увеличениескороститеченияиуменьшениевязкостиприводятквозникновениютурбулентногоре-жиматечения,когдатраекторииотдельныхобъемовжидкостистано-вятсяхаотическими,акартинадвиженияприобретаетнеустойчивыйхарактер.Экспериментыпоказывают,чтопереходвтурбулентныйре-жимтеченияпроисходит,когдапревышенонекотороеопределенноекритическоезначениечислаРейнольдса.Применительнокобтеканию

плоскойповерхностиэтозначениеравноRe_кр

510^5.

Механизмконвективноготеплообменапритурбулентномдвиже-ниисущественноотличаетсяотламинарного.Главноеотличиесостоитвтом,чтотепловуюэнергиюиколичестводвиженияпоперекпотокапереносятмакроскопическиеобъемыжидкости.Хотячастотаперехо-довневелика,нокаждыйизтакихобъемовсодержитогромноеколиче-ствомолекул,врезультатечеготеплообменстановитсязначительноболееинтенсивным,чемприламинарномтечениижидкости.

Втурбулентномтечениитакжесуществуеттепловойпограничныйслой,однакоонгораздотоньше,чемприламинарномрежиме.

Нарис.1.13представленазависимостьтолщиныпограничногослоявдольповерхностипластины.Приееобтеканиипотокомжидко-стиупереднейкромкиобразуетсяламинарныйпограничныйслой,толщинакоторогорастетпомереувеличенияx.ЕгопротяженностьопределяетсякритическимзначениемчислаРейнольдса:

^u0^xкр ₅

Re_{кр }

510.

Далееначинаетсятурбулентныйпограничныйслой,отделенныйотламинарногоучасткаузкойпереходнойобластью.Изменениетемпера-

турыискоростивтурбулентномпограничномслоепроисходитполи-нейномузакону.Толщинапограничногослояивтурбулентномрежи-меувеличиваетсяпомеревозрастанияx,однакозаконвозрастанияиной,чемприламинарномрежиметечения.

y

^u₀ ^u0 ^u0

3

2

1

_xкр ₄ x

Рис.1.13.Изменениетолщиныпограничногослояпривозникновениитурбулентноготечения:

1–ламинарныйпограничныйслой;2–переходнаяобласть;3–турбулентныйпограничныйслой;4–ламинарныйподслой

ЛокальноечислоНуссельтапритурбулентномобтеканииплоскойповерхностиопределяетсяпоследующейформуле[1.17]:

Nu_x0,0296Re^0,8Pr^0,43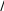_Pr_T

Pr_T

_. (1.4.30)

^x 0 c

Вуравнении(1.4.30)отношениечиселПрандтляпритемпературах

^{жидкостиT}_0

^{иповерхностиT}_c

учитываеттемпературноеизмене-

ниевязкости.Остальныекритериальныечислаопределяютсяпритем-

пературеT_0.ПринебольшихвеличинахразностиT_cT₀

множительв

круглыхскобкахв(1.4.30)можноположитьравнымединице.Среднийкоэффициенттеплоотдачиопределяетсяинтегрированиеманалогичноформуле(1.4.28)иоказываетсяравен:

1,25_xL,

где_xL–локальныйкоэффициенттеплоотдачипри^xL.