4. Конвективныйтеплообмен

Введение

Вгазообразнойижидкостнойсредахпроцессыпередачитеплаго-раздосложнее,чемвтвердомтеле.Переностеплатеперьосуществля-етсянетолькотеплопроводностью(намолекулярномуровне),ноиконвекцией,засчетдвижениясамойжидкости,имеющейтепловойконтактствердымтелом,температуракоторогоотличаетсяоттемпе-ратурыжидкости(далеедлякраткостибудемговоритьтолькоожид-кости).Теплообмен,имеющийдвеуказанныесоставляющие,именует-сяконвективнымтеплообменом[1.15].

Различаютдвавидаконвекции–естественнуюивынужденную.В

естественнойконвекциидвижущаясила,вызывающаяперемещениеобъемовжидкости,вызванатемпературнойзависимостьюплотностижидкости.Типичныйпример–конвекциявчайнике.Нагретыеобъемыводы,находящиесявблизиспирали,имеютменьшуюплотностьивсплываюткповерхности,аихместозанимаетхолоднаявода,котораязатемнагреваетсяиуходитотнагревателяит.д.Происходитсложноедвижениежидкости,вкоторомнарядусмассообменомимеетсяитеп-лообмен.

Вынужденнаяконвекцияпроисходитиз-задействиявнешнейсилы,

заставляющейжидкостьобтекатьповерхностьтела,имеющеготемпе-ратуру,отличнуюоттемпературыжидкости.Примеромможетбытьпереностеплаотстенокмикроканалакжидкости,прокачиваемойче-резнегонасосом.Вынужденнаяконвекцияобеспечиваетболееэффек-тивныйтеплообмен,чеместественная,однакоэтодостигаетсяценойдополнительныхэнергетическихзатрат.

Сенсорытермическогосигналавсегдаработаютвгазовойили

жидкостнойсреде,поэтомуучетконвективноготеплообменаимеетбольшоезначениекакприихпроектировании,такиприэксплуатации.Вэтойсвязинафизическихвопросахконвективноготеплообменане-обходимоостановитьсяподробнее.

1. Основныеособенностиконвективноготеплообмена

Конвективныйтеплообменнеразрывносвязансдвижениемчастицжидкости,которыеодновременносимпульсомпереносятитеплоту.Этонаходитотражениевосновномуравнении,определяющемплот-ностьтепловогопотокавжидкости:

qq_1q_2kТuC_pТ, (1.4.1)гдеиC_p–соответственноплотностьитеплоемкостьжидкостипри

^{постоянномдавлении;u–скоростьдвиженияжидкости;Тиk–}

температураикоэффициенттеплопроводностижидкости.

Первоеслагаемоев(1.4.1)описываеттеплопроводностьпозакону

Фурье,авторое–передачутепла,связаннуюсдвижениемэлементар-ныхобъемовжидкостисоскоростьюu(конвективнаясоставляющая).Физическиэтасоставляющаяпредставляетсобойколичествотепла,переносимоевнаправлениивектораскоростиuчерезединицупо-верхностизаединицувремени.

Сложностьопределенияполяскоростейжидкости

^uu^xyzt^в

конкретныхусловияхвзначительноймереопределяеттрудноститео-ретическогоанализапроцессовконвективноготеплообмена.

Притеоретическомиэкспериментальномопределенииполяскоро-

стейжидкостинеобходимоучитыватьтакоееефундаментальноесвой-ство,каквязкость.

Вязкостьописываетсилысдвига,возникающиевдвижущейсяжидкости.Пустьимеетсядвепластины,междукоторыминаходитсяжидкость,причемоднаизпластиннеподвижна,адругаядвижетсяпа-раллельноейсмалойскоростьюu_0(рис.1.9).

Еслиизмеритьсилу,требуемуюдляподдержанияравномерногодвиженияпластин,тооказывается,чтоонапропорциональнаяплощади

пластиныАиотношению^u0,гдеd–расстояниемеждупластинами:

d

FА^u0. (1.4.2)

d

Коэффициентпропорциональностиименуетсядинамическим^{коэффициентомвязкостижидкостииимеетразмерность}^{Hc/м2.}

u

ПлощадьА

0

F

u

^d Жидкость

u=0

Рис.1.9.Увлечениежидкостимеждудвумяпараллельнымипластинами

Прималыхрасстоянияхмеждупластинамираспределениескоростейэлементарныхобъемовжидкостиноситлинейныйхарактер,причемнанеподвижнойпластинескоростьприлегающегослояиз-заявленияад-гезииравнанулю,u0.

Длямалыхразмеровплощадокирасстояниймеждупластинамииз(1.4.2)получаем:

^F^ux.

А y

Отношение

_F

A

имеетсмыслмеханическогонапряжениясдви-

га,котороевозникаетпридвижениислоевжидкостидруготноситель-

нодруга.

Физическипричинойвязкостиявляетсявзаимодействиемолекул

соседнихэлементарныхобъемовжидкости,втомчислеииз-завоз-можностипереходамолекулизодногообъемавдругой.

Еслидвижениепроисходитвплоскостиивекторскоростиимеетдвекомпоненты,u_u_x,u_y,тонапряжениесдвигаможнопредставить

втензорнойформе

^u ^u_y^

  ^x . (1.4.3)

xy ^_y

x^

 

Втеориитеплообменавместодинамическогокоэффициентавязко-стиобычноприменяюткинематическийкоэффициент,равный

^,



где–плотностьжидкости.Размерностькоэффициентакинематиче-скойвязкостиравна__м²/с.

Диапазонабсолютныхвеличинкинематическойвязкостисущест-

венноменьше,чемдинамической,например,дляводыивоздухапри

20Симеем[1.16]:

дляводы110^3Hс/м^2;

110^6м2/с;

длявоздуха18,110^6Hс/м^2;

1510^6м2/с.

Вязкостьсильнозависитоттемпературы,например,дляводыпе-редточкойзамерзаниякинематическаявязкостьв1,8разавыше,чемпри20С.

Плотностьжидкостивобщемслучаеможетзависетьотскоростиеедвижения.Большинствожидкостейпрактическинесжимаемы.Газыизменяютсвоюплотностьприизменениидавления.Однакоеслиизме-нениядавлениявдольлиниитокамалыискоростьдвиженияэлемен-тарногообъемаприэтоммногоменьшескоростизвука,тогазможносчитатьнесжимаемым.Этоприближениебудетиспользоватьсяпридальнейшемизложенииматериала,посколькусоответствуетреальнымусловиямработыкомпонентовмикросистем.

Вязкостьжидкости,скоростьеедвиженияигеометрияобластипротеканияоказываютрешающеевлияниенарежимтеченияжидко-

сти.Приеемалойскоростидвижения(многоменьшескоростизвука)ивысокойвязкостирежимтеченияламинарный(слоистый).Длянегохарактерныгладкийинепрерывныйхарактерлинийтокаинезавися-щееотвремениполескоростейжидкостипристационарныхвнешнихусловиях.

Прималойвязкости,большойскоростидвиженияинекоторыхособенностяхгеометриипротеканиядвижениежидкостистановится

неустойчивымиламинарныйрежимпереходитвтурбулентный.Вэтомрежиметечениялиниитокатеряютчеткийхарактер,элементар-ныеобъемыжидкостидвижутсяхаотически,совершаянеустойчивыеколебания,интенсивностьперемешиваниячастейобъемажидкости

сильновозрастает.Количественныйкритерийпереходактурбулент-номутечениюжидкостибудетрассмотрендалее.Дляреальныхусло-вийработытермосенсоровикомпонентовмикросистемнойтехникитурбулентныйрежимнехарактерен.

Вязкостьсамымсущественнымобразомвлияетнаполескоростей

жидкости.Нарис.1.10,апоказанораспределениескоростейэлемен-тарныхобъемовжидкости(профильскорости)вкруглойтрубепристационарномтеченииламинарногопотока.Уповерхноститрубыпри-стеночныйслойнеподвижен,однакопомереприближениякоситру-быскоростьвозрастает,посколькутормозящеевлияниестенокумень-шается.Максимальнуюскоростьпотокжидкостиимеетнаоситрубы.

Турбулентноеядро

2r₀

2r₀

u _u

Ламинарныйподслой

а б

Рис.1.10.Полескоростейпритечениижидкостивтрубе:

а–ламинарныйпоток;б–турбулентныйпоток

Наличиенеподвижногослояжидкостивблизиобтекаемойповерх-ностиприводитктому,чтоплотностьтепловогопотокауповерхности(1.4.1)определяетсятолькопервымслагаемым,автороеобращаетсяв^нульu_c^0^{.Экспериментыпоказывают,чтораспределениетемпера-туры}вжидкостиимеетдвачетковыраженныхучастка(рис.1.11).

Первый–сравнительнотонкийслойвблизиповерхности(погра-ничныйслой),гдетемпературныйградиентотличенотнуля(уча-стокI),ивторой,включающийостальную(дальнюю)частьобъемажидкости,гдесуществуетнезначительнаяразницатемператур(участокII).Подобныйтемпературныйходможнообъяснить,предположив,чтовпределахпограничногослоямолекулыжидкостиактивновзаимодейст-вуютсповерхностью,тогдакакзаегопределамихаотическоедвиже-ниечастицжидкостивыравниваетраспределениетемператур.

Впограничномслоепроцесспе- T_{среноса}теплаосуществляетсятепло-проводностьюпозаконуФурье,как

этонаблюдаетсявтвердыхтелах. Однакотеплопроводностьжидкостей

игазовневелика,поэтомунаучастке

Iтепловойпотоквстречаетбольшое ^q

сопротивление.НаучасткеIIтепло

передаетсяконвекциейиэтотпро- ^Tж

цесспроисходитболееинтенсивно,

чемнапредыдущемучастке,поэтому _{0 I II x}

температуравыравнивается.

Такимобразом,дляколичестватеплаq,подводимого(илиотводи-

мого)кединицеплощадиповерхно-стивединицувремени,можнозапи-сать:

Рис.1.11.Распределениетемпе-ратурывжидкостиприпередачетеплаотстенкикжидкости,T_c>T_ж

q^k



^TT_c^{, (1.4.4)}

гдеTиT_c–температурыжидкостинаучасткеIIинаобтекаемойпо-верхности.

Количествопередаваемоготеплавозможноопределить,знаятол-щинупограничногослоя,величинакоторогозависитотмногихфак-

торов,например,отхарактерадвиженияисвойствжидкости,формыповерхностиит.д.Поэтомунапрактикечисленныерасчетыпроводят,

пользуясьотношением^k



безопределенияистиннойвеличиныпогра-

ничногослоя.Этоотношениеназываетсякоэффициентомтеплооб-мена:

^k



(1.4.5)

^{иимеетразмерность}^{Вт/(м2К).Соотношение(1.4.5),такимоб-разом,}принимаетвид

^q^TT_c

(1.4.6)

ипредставляетзаконНьютонадлятеплоотдачисповерхностинагре-тоготела.Учитывая,чтотеплопереносвблизиповерхностиопределя-

^{етсязакономФурье}_u_x00!_^{,из(1.4.6)и(1.4.1)получим}

^^TT_c^k

dT

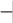^dxx0

, (1.4.7)

адлякоэффициентатеплообменаполучаем:



k dT

. (1.4.8)

TT_c

^dxx0

Уравнение(1.4.7)записанодлятепловогопотокаотповерхноститвердоготелавжидкость(T_сT,рис.1.11)иустанавливаетсвязьме-ждутемпературнымполемжидкостиикоэффициентомтеплопровод-ностииименуетсяуравнениемтеплообмена.

Всемногообразиефакторов,влияющихнаинтенсивностьтеплоот-

дачи,учитываетсяоднимкоэффициентом.Какпоказалиисследова-

ния,этоткоэффициентзависитотскоростидвиженияжидкостиu,

ко-

эффициентатеплопроводности

k,вязкости,

теплоемкости

C_p,

коэффициентаобъемногорасширенияжидкости,температуртвер-доготелаижидкостиT_с,T,отформыФиразмеровтелаl₁,l₂...:

f_u,k,,C_p,,T,T_с,Ф,l₁,l_2.

Большоечисловлияющихфакторовзатрудняетчисленнуюоценкукоэффициентатеплообмена,однакокнастоящемувременисозданрядметодовегоопределения,которыеносятпреимущественноэкспе-риментальныйхарактер.