
- •Зябиров Али Хайдарович Тема №1: «Обнаружение сигналов».
- •Тема №2: «Прием сигналов как статистическая задача».
- •Принятие решения на основе анализа этой вероятности
- •Тема №3 «Функция правдоподобия».
- •Отношение правдоподобия
- •Корреляционный прием. П ринимаемый сигнал
- •Оптимальная фильтрация.
- •Импульсное представление.
- •Частотное превставление.
- •Качественные показатели оптимального приёмника обнаружения.
- •Тема №6. Сигнал со случайной начальной фазой.
- •Оптимальная фильтрация
- •Качественные показатели оптимального приемника обнаружения сигнала со случайной начальной фазой.
- •Тема №7. Сигнал со случайной амплитудой и начальной фазой.
- •Качественные показатели оптимального приемника обнаружения для сигнала со случайной начальной фазой и амплитудой.
- •Качественные показатели устройства оптимальной обработки пачек когерентных радиоимпульсов. Общая характеристика пачек когерентных импульсов.
- •Сигнал в виду нефлуктуирующей пачки когерентных радиоимпульсов.
- •Сигнал в виде флуктуирующей пачки когерентных импульсов.
- •Структура устройств оптимальной обработки пачек когерентных импульсов. Структура оптимального фильтра.
- •Оптимальная фильтрация
- •Структура устройств оптимальной обработки широкополосных радиоимпульсов. Пачка фазоманипулированных радиоимпульсов.
- •Нефлуктуирующая пачка.
- •Флуктуирующая пачка.
- •Устройство оптимальной обработки пачек некогерентных радиоимпульсов.
- •Понятие среднего риска и статистические критерии обнаружения.
Качественные показатели оптимального приёмника обнаружения.
Вне зависимости от способа реализации оптимального приёмника процедура принятия решения заключается в сравнении корреляционного интеграла с пороговым уровнем. В отсутствии шумов корреляционный интеграл может принимать лишь 2 значения:
 ,
вероятность ложной тревоги =0.
,
вероятность ложной тревоги =0.
Вероятность обнаружения=1, ложной тревоги=0. При наличии шума корреляционный интеграл становится случайной величиной, поэтому вероятности пропуска цели и ложной тревоги принимают некоторые конечные значения. Они определяются отношением энергии сигнала к спектральной плотности шума. Для подсчёта этих вероятностей необходимо знать закон распределения корреляционного интеграла. Корреляционный интеграл подчиняется нормальному закону распределения, так как представляет собой линейное преобразование нормального случайного процесса.
Определению подлежат математическое ожидание и дисперсия корреляционного интеграла.
Математическое ожидание при наличии сигнала:


Дисперсия корреляционного интеграла с точностью до постоянного множителя = дисперсии флуктуации на входе согл-го фильтра.

где Е-энергия сигнала.
Заметим, что дисперсия всегда опред-ся этим выражением в независимости от того, присутствует или отсутствует полезный сигнал. Плотность вероятности нормальной случ-й вел-ны при наличии сигнала опред-ся:

При отсутствии сигнала:
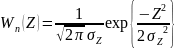
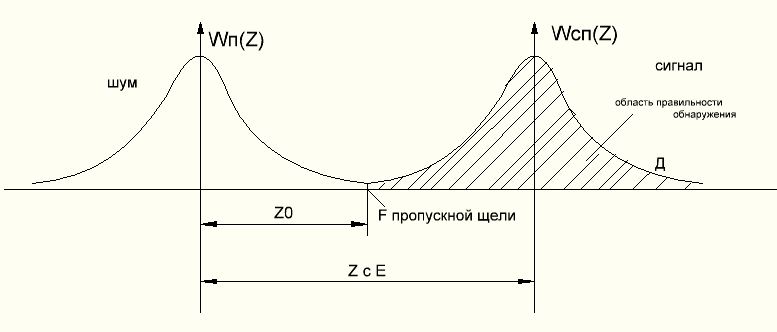
Рис.6
 – область правильного обнаружения,
– область правильного обнаружения,
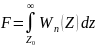 – ложная тревога,
– ложная тревога,
 - интеграл вероятности.
- интеграл вероятности.
 - вероятность правильного обнаружения.
- вероятность правильного обнаружения.
Таким образом вероятность ложной тревоги = отношению порогового уровня к эффективному значению флуктуации корреляционного интеграла. Вероятность правильного обнаружения зависит и от отношения энергии ожидаемого сигнала к Ϭz. Это отношение совпадает с отношением сигнал- помеха на выходе согласованного фильтра. Величина q- параметр обнаружения.
 ,
введем обозначение
,
введем обозначение
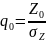 .
.
 - при постоянномF и
- при постоянномF и
 будем называть характеристиками
обнаружения.
будем называть характеристиками
обнаружения.

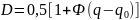
Нарисуем семейство характеристик обнаружения:

Рис.7
Характеристики обнаружения позволяют найти минимальную энергию сигнала, необходимую для достижения заданного значения D при фиксированном F. Определив по кривым значение qmin по заданным Dи F, находим минимальную энергию сигнала, обеспечивающую заданную надежность обнаружения.


τс- длительность сигнала.
Качественные показатели оптимального приемника обнаружения могут быть найдены из хар-к обнаружения. Для сигнала с известными параметрами зависит только от энергии сигнала и не зависит от формы сигнала.
Тема №6. Сигнал со случайной начальной фазой.
Если все параметры сигнала известны и начальная фаза тоже, функция правдоподобия записывается следующим образом:
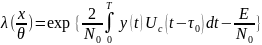
 - Отношение правдоподобия вычисляется
для определенного значения начальной
фазы радиоимпульса.
- Отношение правдоподобия вычисляется
для определенного значения начальной
фазы радиоимпульса.
Рассматривается сигнал с неизвестной начальной фазой: (3)

Начальная фаза может
принимать любые значения [0,2π]. Т.к. при
обнаружении подлежит там факт наличия
или отсутствия сигнала в не зависимости
от значения начальной фазы. В этом случае
отношение правдоподобие может быть
вычислено как среднее по всем возможным
значениям начальной фазы:
 ,
где p(θ) –априорное
распределение начальной фазы. Т.к. фаза
изменяется от [0,2π], то:
,
где p(θ) –априорное
распределение начальной фазы. Т.к. фаза
изменяется от [0,2π], то:
 .
.
Теперь подставляем все и находим отношение правдоподобия с начальной случайной фазой:
 .
.
Следовательно, корреляционный интеграл записывается:
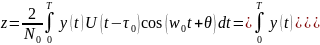

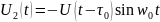
 ,
,
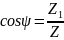 ,
,

Учитывая все предыдущие записи, запишем корреляционный интеграл:
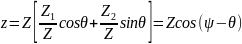
Т.к. энергия сигнала практически не зависит от начальной фазы, поэтому записываем, что она равняется Е:

Учитывая это, отношение правдоподобия примет вид:

В квадратных
скобках указана модифицированная
функция Бесселя первого рода нулевого
порядка аргумента
 .
.
Учитывая функцию Бесселя, получим:

Находим Z:
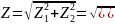
Структурная схема:
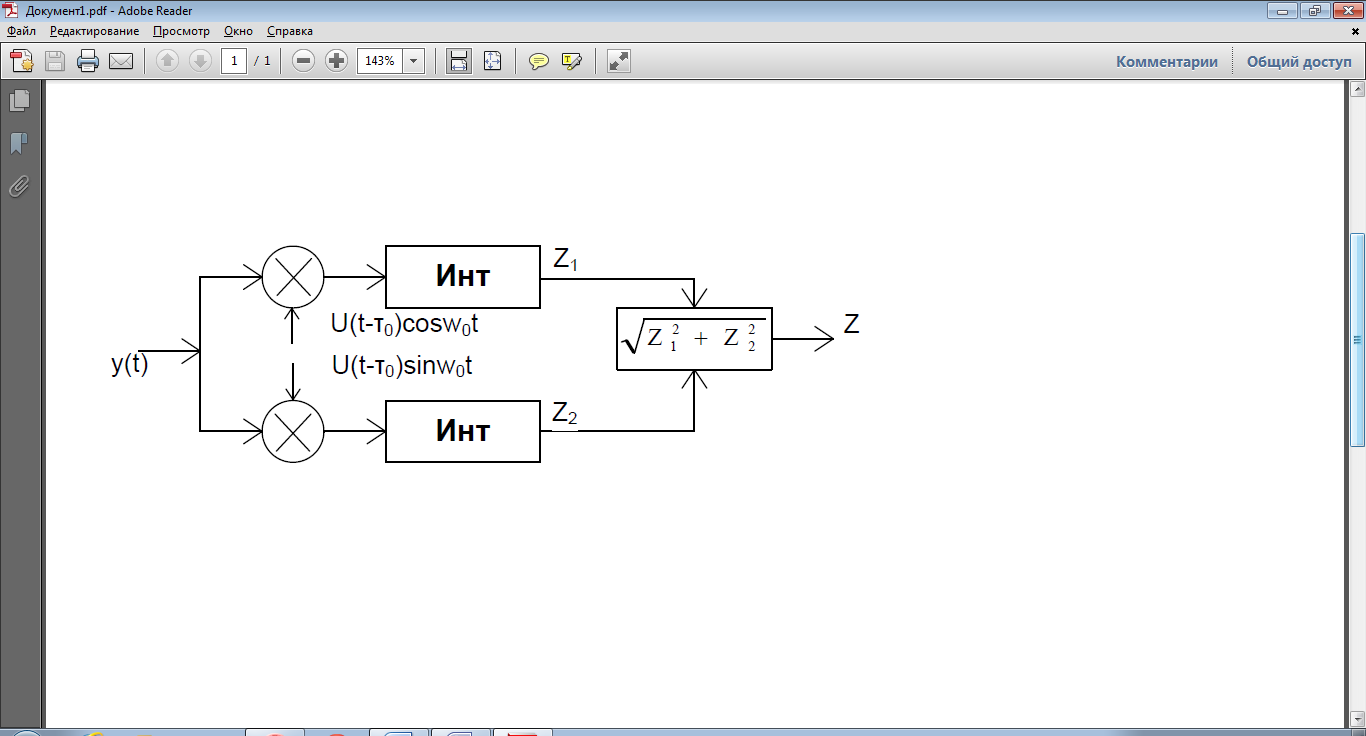
Принятая реализация y(t) поступает на два параллельных канала sin и cos. Каждый канал содержит умножитель и интеграл. В качестве опорных напряжений умножителя, использованы сдвинутые на 90 градусов относительно друг друга радиоимпульсы (sin и cos). Огибающая каждая из них идентична огибающая ожидаемого сигнала. После интегрирования результатом перемножения образуется величины z1 и z2. Вычислительное устройство возводит в квадрат, суммирует и извлекает квадратный корень, на выходе получаем корреляционный интеграл. Далее сравниваем с пороговым значением и принимаем решение: если Zпревышает пороговое значение z0, то принимается решение, что сигнал есть, если меньше – сигнала нет.
Рассматриваемый способ обработки сигнала называется корреляционным приемом с двумя квадратурными каналами (sin и cos). Наличие двух квадратурных каналов исключает возможность пропуска сигнала за счет незнания начальной фазы. Если на выходе одного канала фаза равна нулю, то другой даст нам единицу.
