2.2. Релаксационные процессы.

Экспериментально установлено, что деформации и напряжения, возникающие в полимерах и в композиционных материалах на их основе, зависят не только от величины действующих нагрузок и условий нагружения, но и от времени. Процессы изменения деформаций и напряжений во времени называют релаксационными. Основными видами релаксационных процессов являются ползучесть и релаксация.

Ползучесть– это процесс роста деформации во времени при постоянном напряжении. При этом полагают, что все прочие условия (температура, направление внешних нагрузок, среда, в которой происходит деформирование) остаются неизменными. Типичный вид кривой ползучести - зависимость деформации -  от времени t при постоянном напряжении  - представлен на рис. 2.3.

Кривую ползучести получают по результатам испытаний образцов из исследуемого материала. Форму образцов и способы приложения к ним нагрузки обычно выбирают такими, чтобы в рабочей части образца было создано однородное поле напряжений (одноосное напряженное состояние, чистый сдвиг). Последнее условие необходимо для отождествления свойств материала образца со свойствами элементарного объема полимерного тела, находящегося под нагрузкой. Простейшими являются испытания на центральное растяжение или сжатие образцов призматической или цилиндрической формы в статическом режиме нагружения. Для случаев малых деформаций изменениями абсолютных размеров образцов можно пренебречь и проводить испытания не при постоянном напряжении, а при постоянной силе. Практически реализовать мгновенное статическое нагружение невозможно, поэтому нагрузку прикладывают с некоторой конечной скоростью. В этом случае за деформацию, соответствующую моменту времени t, обычно принимают деформацию, измеренную сразу после того, как нагрузка достигнет своего конечного значения. Ординату точки А на рис. 2.3. обозначают и называют мгновенной деформацией, что в какой-то мере условно, т.к. в процессе нагружения уже начинает развиваться деформация ползучести.

После полного приложения нагрузки происходит увеличение деформации , при этом скорость её изменения деформации во времени монотонно убывает до некоторой минимальной величины. В связи с этим ползучесть на участке АВ называют неустановившейся. Стабилизация скорости изменения деформации наблюдается на участке ВС, что соответствует установившейся ползучести. Если испытываемый материал проявляет хрупкое разрушение, то испытание заканчивается разрушением образца в момент времени, соответствующем абсциссе точки С. При пластическом характере разрушения, которое сопровождается образованием шейки, на диаграмме растяжения появляется участок CD.В этом случае разрушение происходит в момент времени, соответствующем точке D. Время, в течение которого образец находился под нагрузкой вплоть до момента его разрушения, называют долговечностью материала, о чем более подробно будет сказано впоследствии.

Если в некоторый момент времени ti полностью снять действующую на образец нагрузку, то деформация , накопленная к этому моменту времени, мгновенно уменьшится на величину , после чего будет идти ее дальнейшее уменьшение с течением времени (рис. 3.2.). Процесс изменения деформации во времени, которое происходит с момента приложения нагрузки (увеличение деформации), носит название прямого последействия, а процесс ее изменения во времени сразу же после полной разгрузки образца (уменьшение деформации) называют обратным последействием.

Последействие называют упругим, если деформации после снятия нагрузки полностью исчезают с течением времени, и пластическим, когда остаточная деформация не равна нулю.

Кривые ползучести, изображенные на рис. 2.3 и 2.4, являются в определенной степени условными. Многочисленными экспериментами установлено, что вид кривой ползучести в значительной степени зависит не только от природы материала, но и от условий испытания. Среди них наиболее существенными являются уровень механического напряжения, температура и среда, в которой находится испытываемый образец.

На рис. 2.5 представлены кривые ползучести, полученные при различных уровнях напряжений.

При малых уровнях напряжений, соответствующим 10–20 процентам от разрушающего напряжения , процесс деформирования сопровождается плавным уменьшением скорости ползучести и асимптотическим стремлением деформации к некоторому предельному значению (кривая 1). С увеличением напряжения происходит увеличение деформации и уменьшение долговечности материала. При этом вид кривой ползучести изменяется (кривые 2,3,4), что выражается в постепенном сокращении участка установившейся ползучести, который уже практически полностью исчезает при уровнях напряжений, приближающихся к разрушающему напряжению для испытываемого материала.

Аналогичный вид имеют кривые ползучести, полученные при сжатии и чистом сдвиге (изгиб).

Чтобы определить характер ползучести полимера, строят изохроны, которые представляют собой зависимость напряжение-деформация при фиксированном значении времени. Для построения изохрон проводят испытания нескольких образцов при различных уровнях напряжений (рис. 2.6a). После этого, при фиксированном времени t, определяют величины деформаций и соответствующих им напряжений. График зависимости , построенный для момента времени t, называется изохроной параметра t(рис. 2.6б). Аналогичным образом можно построить изохроны других параметров времени.

Если изохроны всех параметров представляют собой прямые линии, т.е. увеличение деформации идет прямо пропорционально увеличению напряжения, то характер ползучести в исследуемом диапазоне напряжений и деформаций является линейным, в противном случае ползучесть является нелинейной. На рис. 2.7aи 2.7б показаныизохроны линейно-ползучего и нелинейно-ползучего материалов соответственно.

Следует отметить, что изохрону параметра (t=0) практически получить невозможно, по указанным выше причинам. Однако известно,что при мгновенном нагружении полимеры проявляют линейно-упругие свойства, поэтому изохроны параметра , должны представлять собой прямые линии, как для линейно-ползучего, так и для нелинейно-ползучего материалов.

Экспериментально установлено, что деформационные характеристики полимеров существенно зависят от температуры, которая определяет его физическое состояние. Если полимер находится в твердом состоянии, то он проявляет свойства, сходные с описанными выше. При этом увеличение температуры, как правило, приводит к увеличению деформации и ускорению процесса ползучести. Тем не менее, для полимеров, находящихся в высокоэластическом состоянии (в некоторых температурных диапазонах), имеет место увеличение упругих констант при увеличении температур, что ведет к снижению деформации.

Развитие процессов ползучести в полимерных материалах вызывает необходимость в зависимость «напряжение – деформация» введения третьей переменной величины – времени. Расчетами развития деформации во времени занимается теория ползучести. Существуют различные гипотезы ползучести, носящие чисто феноменологический характер, т.к. они не опираются на исследования структуры материала и не имеют физически обоснованных предпосылок. Тем не менее, во многих случаях они дают возможность проводить достаточно корректные расчеты конструкций из полимерных материалов.

Явление ползучести характеризуется многими параметрами: температурой, напряжениями, деформациями, их производными во времени, константами материала, средой, в которой эксплуатируется материал и др. Эти параметры связаны между собой некоторой функцией:

(2.2.)

Для различных материалов и различных видов нагружения некоторые параметры этой функции сказываются менее существенно, чем другие. Это позволяет значительно упростить вид функции. Принимая разные группы параметров за основные, получают содержание той или иной гипотезы (теории) ползучести. Наиболее простыми формами связи параметров функции (2.2.) являются уравнения, связывающие по три важнейшие параметра.

Если записать уравнение (2.2.) в таком виде:

(2.3.),

полагая, чтоТ=const, то получится уравнение теории упрочнения. В этом уравнении время не содержится в явной форме, а выражается через скорость деформирования. Одной из аналитических записей этой теории является функция:

(2.4.),

где α и b- коэффициенты; пластическая составляющая полной относительной деформации ( .

Согласно другой гипотезе – теории течения, – при постоянной температуре существует зависимость:

(2.5.).

Наиболее распространенной аналитической зависимостью пластической деформации от напряжения и времени является уравнение следующего вида:

(2.6.),

где n-коэффициент для каждого материала, зависящий от температуры; B-функция времени и температуры.

По гипотезе течения в записи (2.6.), как и по гипотезе упрочнения (2.4.), кривые прямого последействия являются геометрически подобными.

Третья гипотеза – теория старения- предполагает, что при определенной температуре между пластической деформацией , напряжением и временем существует постоянная зависимость:

(2.7.).

Такое предположение физически не является обоснованным. В самом деле, при снятии нагрузки, вызвавшей пластическую деформацию, деформация исчезает во времени, как это видно на рис. 2.4. По гипотезе старения пластическая деформация при отсутствии напряжения равна нулю. Тем не менее эта гипотеза получила большое распространение, и в ряде случаев расчеты, выполненные по ней, дают не только качественно, но и количественно правильные результаты. Одним из аналитических выражений гипотезы старения является уравнение:

(2.8.),

гдеА и n - коэффициенты.

Все три гипотезы ползучести недостаточно физически обоснованы и не описывают явления обратного последействия и применимы только в случае активного нагружения.

Более физически обоснованной, позволяющей учитывать явление обратного последействия, является теория наследственности. Она базируется на принципе суперпозиции, предложенном австрийским физиком Больцманом в работах по изучению свойств полимерных материалов, и развита в дальнейшем итальянским математиком и физиком Вольтерра. Она учитывает историю нагружения (разгружения) и в этом смысле является более полной, однако расчетные зависимости ее довольно громоздки.

Теория наследственности основывается на следующих соображениях. Полная деформация вязкоупругого тела в момент времени t складывается из мгновенной деформации, определяемой напряжением t, действующим в данный момент времени, и равной to , и наследуемой деформации, накопленной в теле к моменту времени t за счет ползучести. Величина этой деформации должна быть пропорциональной величине напряжения S),приложенного в некоторый момент времени действия этого напряжения tS, и некоторой функции K(tS). При этом функция K(tS) должна быть монотонно убывающей, чтобы «изгладить воспоминания» о воздействии напряжения S) с течением времени. Материал как бы помнит предыдущие воздействия.

Аналитическая зависимость между напряжением и деформацией по этой гипотезе записывается следующим образом:

(2.9.)

аналогично для напряжений:

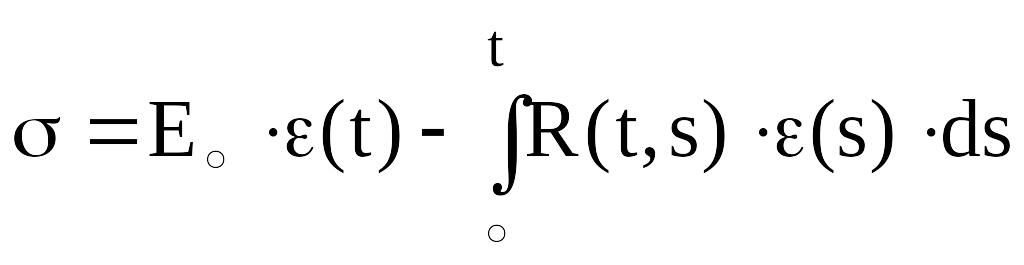(2.10.)

где мгновенные деформация и напряжение,

K,R-некоторые функции времени,

s-переменная интегрирования (время действия напряжения или деформации), tтекущее время

мгновенный модуль упругости.

Функции K и R называют ядрами интегральных уравнений. Уравнение (2.9.) является линейным уравнением второго рода и носит имя «уравнение Вольтерра». Функцию К(t получают, проводя интегрирование кривой ползучести t по времени.

Релаксация – это процесс изменения напряжений во времени при постоянной деформации и при неизменных прочих условиях. На рис. 2.8 представлена типичная кривая релаксации. В первом приближении ее можно описать с помощью уравнения:

(2.11.).

В момент приложения нагрузки, вызывающей деформацию , в образце возникает начальное напряжение o, после чего величина напряжения уменьшается и при неограниченном увеличении времени стремится к некоторому значению , при этом величина деформации остается постоянной. При t ( Время , в течение которого релаксирующая величина t уменьшается в ℮ раз, называется временем релаксации. Следует отметить, что для большинства полимеров величина близка к нулю.

Кривую релаксации получают по результатам испытаний образцов. Исследования на релаксацию сопряжены с трудностями по регистрации напряжений.

Анализ результатов экспериментов на ползучесть и релаксацию, позволяет сделать вывод, что полимерные материалы можно рассматривать как материалы с изменяющимися во времени деформационными характеристиками, которые являются аналогами упругих констант, используемых в традиционных курсах сопротивления материалов.

Это можно проиллюстрировать графиком зависимости отношения , которое определяет некоторый модуль упругости полимерного материала, от времени (рис. 2.9). Значения  при t и t называют соответственно мгновенным o и длительным E модулями упругости, а все остальные (промежуточные) значения , соответствующие текущим значениям времени t, называют текущими модулями упругости и обозначают .

В заключение раздела о релаксационных процессах необходимо подчеркнуть, что аппроксимация уравнений ползучести простыми аналитическими функциями типа (2.8.) не всегда возможна. В некоторых случаях удобно проводить расчеты численным или графоаналитическим методами с использование кривых ползучести, полученных экспериментально.

В качестве примера графоаналитического метода расчета рассмотрим задачу по релаксации напряжений в детали, подвергнутой растяжению с постоянной деформацией.

Необходимо определить время работы прокладки из полимерного материала (срок ее службы до нарушения герметичности соединения). Прокладка в результате затяжки фланцев получила относительную деформацию . Свойства материала заданы кривыми ползучести (рис. 2.10 а.).

Рассчитаем начальную относительную деформацию прокладки по заданной величине  и толщине прокладки : o =. Далее, проведем на рис. 2.10, горизонталь от точки, соответствующей . Точки пересечения этой горизонтали кривых ползучести будут соответствовать моментам времени t1, t2, t3 и т.д., когда в прокладке устанавливаются напряжения 1 ,2 ,3 и т.д. По полученным значениям напряжений строим кривую релаксации t (рис. 2.10,б). Отложив на этом графике ординату, равную и проведя от нее горизонталь до пересечения с кривой релаксации, определим искомую величину .