Лекции по математическому анализу_1 / Лекция 32

Лекция 32. Ряды Фурье.

П.1 Линейные пространства со скалярным произведением.

ОПР. Множество элементов называют линейным пространством, если в нем введены операции сложения и умножения на скаляр, удовлетворяющие 8 аксиомам : и 1) 2) 3) ,

4) , 5) , 6) 7) ,

8) .

ОПР. Линейное пространство E называют евклидовым, если в нем введена операция (скалярное произведение), удовлетворяющая 5 аксиомам : ,

1) 2) 3) 4) ,

5) .

ОПР. Элементы ортогональны, если .

ОПР. Нормой элемента (длиной) называют число . Нулевую норму имеет только нулевой элемент. Норма положительна, если .

Справедливы следующие соотношения : 1) . 2) ,

3) ( неравенство треугольника).

ПРИМЕРЫ евклидовых пространств.

1. - n - мерное арифметическое пространство: .

Операции сложения и умножения на число – покоординатные. Скалярное произведение :

, норма элемента .

2. - пространство числовых последовательностей, , , для которых

ряд сходится. Операции сложения и умножения на число – покоординатные. Скалярное произведение : . Сходимость ряда для любых следует из неравенства : при (критерий Коши).

3. - пространство непрерывных , 2- периодических функций с условием . Последнее условие означает, что функции являются непрерывными, периодическими на всем R . Операции сложения и умножение на скаляр – поточечные .Норма элемента определяется .

4. - пространство кусочно- непрерывных, 2- периодических функций , т.е. на отрезке существует конечное число точек

в которых функция имеет разрывы первого рода. Норма элемента определяется . Даже если функция непрерывна на , но , то

то ее продолжение на R не является непрерывным на R .

5. - пространство 2- периодических функций с интегрируемым квадратом на . Скалярное произведение определяется формулой, а норма .

6. - пространство абсолютно интегрируемых на , 2- периодических функций , т.е. существует интеграл , возможно, в несобственном смысле , абсолютно сходящийся. Норма определяется формулой .

ОПР. Последовательность элементов E называется фундаментальной, если

,

т.е. для нее выполняется критерий Коши.

ОПР. Последовательность элементов E называется сходящейся, если существует элемент , для которого , т.е. .

ОПР. Пространство E называется полным, если всякая фундаментальная ее последовательность сходящаяся.

Полнота пространства в примере 1 следует из критерия Коши для R , сходимость последовательности по норме пространств примеров 3,4 равносильна равномерной сходимости на отрезке и , по доказанному ранее, их пределы – непрерывные функции, т.е. пространства и полные. Пространства и в примерах 5,6 полными не являются.

ПРИМЕР. Множество Q – рациональных чисел на отрезке счетное, поэтому

. Рассмотрим последовательность функций из : ( продолжается на R 2- периодической функцией ).

Так как отлична от нуля на только в конечном числе точек, для любого n . Она фундаментальна, поскольку для любого . Однако,

Пределом такой функции является функция , которая не интегрируема по Риману на отрезке и не принадлежит .

П.2 Ортогональные системы функций.

ОПР. Система функций в E называется ортонормированной , если

.

Опр. Для каждого можно составить ряд с коэффициентами , который называется рядом Фурье элемента x по ортогональной системе .

Ряд Фурье сходится, если последовательность его частичных сумм сходящаяся.

Является ли x суммой его ряда Фурье ? В общем случае это не так и дальнейшее проясняет условия, при которых ответ на этот вопрос утвердительный.

МИНИМАЛЬНОЕ СВОЙСТВО частичных сумм ряда Фурье.

Рассмотрим линейную комбинацию первых n членов ортогональной системы с произвольным набором коэффициентов : . Докажем, что , где - коэффициенты ряда Фурье.

ДОК.

.

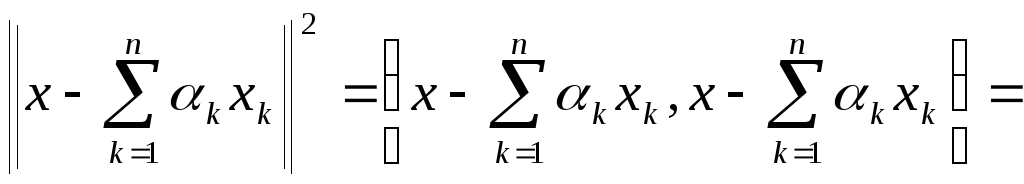
Отсюда следует, что минимальному значению соответствуют .

СЛЕДСТВИЕ 1. Ряд из квадратов коэффициентов Фурье сходится.

Действительно, , т.е. частичные суммы ряда ограничены и ряд сходится.

СЛЕДСТВИЕ 2. Коэффициенты Фурье убывают с ростом n .

СЛЕДСТВИЕ 3. - неравенство Бесселя.

ТЕОРЕМА 1. Если E – полное нормированное пространство и -ортонормированная система в E , то ряд Фурье элемента x сходится, причем его сумма , обладает свойством : для любого k .

ДОК. Для частичных сумм ряда Фурье .

Из сходимости ряда следует, что .

т.е. последовательность фундаментальная и в полном пространстве имеет предел . Тогда .

ОПР. Ортонормированная система элементов называется замкнутой, если не существует ненулевого элемента в E , перпендикулярного каждому , т.е.

из условия .

ТЕОРЕМА 2. Если E - полное нормированное пространство, а - замкнутая ортонормированная система элементов в E , то ряд Фурье элемента по системе сходится и имеет x своей суммой.

ДОК. По теореме 1 элемент перпендикулярен каждому элементу

Тогда из условия замкнутости .

ТЕОРЕМА 3. Если - коэффициенты ряда Фурье элемента x полного пространства E , то имеет место равенство Парсеваля : .

ДОК. По теореме 2 ряд Фурье элемента x сходится, т.е. или , т.е.

.

ВОПРОСЫ К ЭКЗАМЕНУ.

1. Линейные пространства со скалярным произведением. Примеры.

2. Ортонормированные системы и ряды Фурье. Минимальное свойство частичных сумм рядов Фурье. Неравенство Бесселя.

3. Сходимость ряда Фурье по ортонормированной системе элементов в полном нормированном пространстве E . Свойства суммы ряда Фурье.

4. Замкнутые ортонормированные системы. Теорема о сходимости ряда Фурье по замкнутой ортонормированной системе элементов в полном нормированном пространстве.

Равенство Парсеваля.