Какие взаимодействия относятся к фундаментальным? На каких расстояниях проявляются фундаментальные взаимодействия? Какова относительная интенсивность фундаментальных взаимодействий?
Фундаментальные воздействия
1)слабое (менее 10-15) интнесивность – 10-13
2)сильное (менее 10-15) интнесивность – 1
3) Электростатическое (от 0 до беконеч.) интнесивность – 10-2
4) Гравитационное (от 0 до беконеч.) интнесивность – 10-38
Определение момента импульса материальной точки и момента силы. Проекция векторов момента импульса и момента силы на выбранную ось Уравнение моментов для материальной точки. При каких условиях сохраняется момент импульса материальной точки?
Момент силы — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Моментом импульса материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
L = [rp] = [r,mv],
где г — радиус-вектор, проведенный из точки О в точку А; р = mv — импульс
Вектор 
будет
направлен вдоль нормали
к плоскости, образованной
векторами 
и 
,направление
которого определяется по
правилу буравчика.
Условие сохранения - остается постоянной, пока на систему не воздействуют внешние силы
Система материальных точек. Вывод уравнения движения системы материальных точек на примере двух жестко связанных тел(хз)
Системой материальных точек называется такая их совокупность, в которой положение и движение каждой точки зависит от положения и движения всех точек данной системы. Часто систему материальных точек называют механической системой.
Центр масс системы материальных точек. Определение радиус-вектора центра масс. Свойства центра масс. Скорость центра масс. Вывод уравнения движения центра масс. Закон сохранения координаты центра масс системы материальных точек.
Цен-
тром масс (или центром инерции)
системы материальных точек называет-
ся воображаемая точка С, положение
которой характеризует распределение
массы этой системы. Ее радиус-вектор
равен
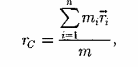
Центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным.
Скорсть центра масс
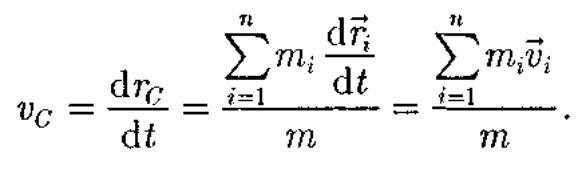
Для
непрерывного распределения массы с
плотностью r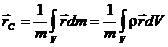 
.
Если силы тяжести, приложенные к каждой
частице системы, направлены в
одну сторону,
то центр масс совпадает с центром
тяжести. Но если 
не
параллельны,
то центр масс и центр тяжести не
совпадают.
Взяв производную по времени
от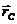 
,
получим:
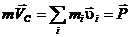т.е. полный
импульс системы равен произведению ее
массы на скорость центра масс.
Подставляя
это выражение в закон изменения полного
импульса, находим:
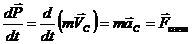Центр
масс системы движется как частица, в
которой сосредоточена вся масса системы
и к которой приложена результирующая внешних сил.
При поступательном движении все точки твердого тела движутся так же, как и центр масс (по таким же траекториям), поэтому для описания поступательного движения достаточно записать и решить уравнение движения центра масс.
Так
как 
,
то центр масс замкнутой
системы должен
сохранять состояние покоя или равномерного
прямолинейного движения, т.е. 
=const.
Но при этом вся система может вращаться,
разлетаться, взрываться и т.п. в результате
действия внутренних
сил.
Rс(t1) = Rc(t2) закон сохранения координаты центра масс
Работа потенциальных (консервативных) силы на примере силы тяжести. Определение потенциальных (консервативных) силовых полей. Введение понятия потенциальной энергии через работу силы. Связь силы и потенциальной энергии
Потенциальная сила - сила, работа к-рой зависит только от начального и конечного положения точки её приложения и не зависит ни от вида траектории, ни от закона движения этой точки. Консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0. Потенциальное (консервативное) силовое поле:Потенциальным называется поле, работа которого при переходе из одной точки поля в другую не зависит от формы траектории. Потенциальными являются поле силы тяжести и электростатическое поле. Введения понятия потенц. Энергии через работу сил - Потенциальная энергия — скалярная физическая величина, характеризует запас энергии некоего тела (или материальной точки), находящегося в потенциальном силовом поле, который идет на приобретение (изменение) кинетической энергии тела за счет работы сил поля. Связь силы и потенциальной энергии - Каждой точке потенциального поля соответствует некоторое значение силы , действующей на тело, и некоторое значение потенциальной энергии U. Значит, между силой и U должна быть связь , с другой стороны, dA = –dU,