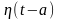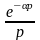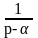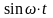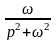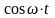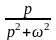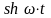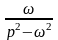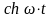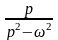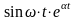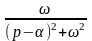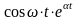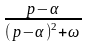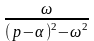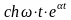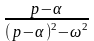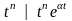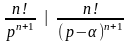- •1 Поняття про числовий ряд і його суму.Необхідна умова збіжності ряду. Гармонічний ряд. Залишок ряду. Властивості збіжних рядів
- •2 Ознаки збіжності числових рядів з додатними членами
- •3. Ознака д’Аламбера. Радикальна та Інтегральна ознаки Коші.
- •4 Знакозмінні ряди. Ознака Лейбніца.
- •5 Знакозмінні ряди. Абсолютно і умовно збіжні ряди, їх властивості.
- •6 Функціональні ряди.
- •7 Властивості рівномірно збіжних рядів
- •8 Степеневі ряди. Властивості степеневих рядів.
- •9. Ряд Тецлора і Маклорен
- •10. Умови Дірихле розкладу ф-ції в ряд Фурє. Ряд Фур’є для парних і непарних ф-й.
- •11. Умови Дірихле розкладу ф-ції в ряд Фурє. Ряд Фур’є для ф-ї періоду
- •12 Інтеграл Фур’є для парних і непарних ф-й. Синус і косинус перетворення Фур’є.
- •13,14 Функція комплексної змінної. Границя. Неперервність. Основні елементарні ф-ї кз:
- •17 Диференціювання ф-ї комплексної змінної (фкз). Умови Коші-Рімана
- •18. Теорема Коші для однозв’язної області Теорема Коші для багатозв’язної області
- •20. Класифікація ізольованих особливих точок ф-ї.
- •21 Ряд Лорана. Теорема про розвинення ф-ї в кільці.
- •22. Означення лишку аналітичної функції в ізольованій особливій точці. Обчислення лишків в особливих точках.
- •23 Означення функції-оригіналу. Означення перетворення Лапласа. Теорема існування. Необхідна умова існування зображення.
21 Ряд Лорана. Теорема про розвинення ф-ї в кільці.
Ряд
вигляду
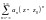 називається рядом Лорана в околі точки
називається рядом Лорана в околі точки
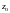 або по степенях
або по степенях
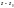 ,
при цьому ряд Лорана є сумою рядів:
,
при цьому ряд Лорана є сумою рядів:
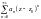 -
правильна частина ряду Лорана;
-
правильна частина ряду Лорана;
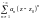 -
головна частина ряду Лорана.
-
головна частина ряду Лорана.
Ряд
Лорана вважається збіжним в точці
 ,
якщо одночасно існують границі:
,
якщо одночасно існують границі:
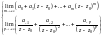
Форма
області збіжності ряду Лорана визначається
тим, що його правильна частина є збіжною
у крузі
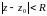 ,
а головна частина у зовнішності круга
,
а головна частина у зовнішності круга
 .
Таким чином обл. збіжності ряду Лорана
є кільце з центром в точці
.
Таким чином обл. збіжності ряду Лорана
є кільце з центром в точці
 внутрішній радіус якого
внутрішній радіус якого
 а зовнішній
а зовнішній
 .
Якщо
.
Якщо
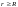 то обл. збіжності такого ряду не
досліджується.
то обл. збіжності такого ряду не
досліджується.
Частинними випадками є:
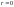 обл.
збіжності являє собою круг з виколотим
центром;
обл.
збіжності являє собою круг з виколотим
центром;
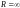 обл.
збіжності являє собою зовнішність
круга.
обл.
збіжності являє собою зовнішність
круга.
Теорема:
Нехай ф-я
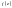 є однозначною та аналітичною в кільці
є однозначною та аналітичною в кільці
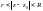 тоді ця ф-я може бути представлена у
вигляді суми ряду Лорана:
тоді ця ф-я може бути представлена у
вигляді суми ряду Лорана:
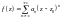 ,
де
,
де
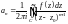
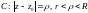 - коло
концентричне з даним кільцем.
- коло
концентричне з даним кільцем.
22. Означення лишку аналітичної функції в ізольованій особливій точці. Обчислення лишків в особливих точках.
Означення:
Лишком аналітичної функції називається
коефіцієнт
 її Лоранівського розкладу.
її Лоранівського розкладу.
Лишки обчислюються в залежності від класифікації особливих точок:
Якщо
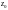 точка аналітичності або усувна особлива
точка, то лишок нульовий.
точка аналітичності або усувна особлива
точка, то лишок нульовий.
Якщо
точка
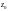 є простим полюсом, то лишок обчислюється
наступним чином:
є простим полюсом, то лишок обчислюється
наступним чином:
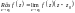 .
У випадку якщо ф-я
.
У випадку якщо ф-я
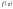 має наступний вигляд
має наступний вигляд
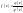 ,
то лишок можна обчислити за формулою
,
то лишок можна обчислити за формулою
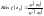 ,
де
,
де
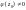 ,
,
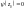 ,
,
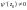 .
.
Якщо
точка
 є полюсом порядку
є полюсом порядку
 ,
то лишок обчислюється наступним чином:
,
то лишок обчислюється наступним чином:
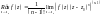
Якщо
 є істотно особлива точка, то лишок має
наступний вигляд.
є істотно особлива точка, то лишок має
наступний вигляд.
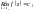
23 Означення функції-оригіналу. Означення перетворення Лапласа. Теорема існування. Необхідна умова існування зображення.
Ф-я
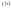 називається оригіналом, якщо вона
задовольняє наступним вимогам:
називається оригіналом, якщо вона
задовольняє наступним вимогам:
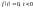
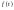 -
неперервна при
-
неперервна при
 за винятком можливо скінченої кількості
точок розриву першого роду на кожному
скінченому інтервалі
за винятком можливо скінченої кількості
точок розриву першого роду на кожному
скінченому інтервалі
існують
такі числа
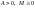 ,
що
,
що
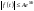
Означення:
інтегральний оператор , який переводить
функцію-оригінал
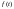 у функцію-зображення
у функцію-зображення
 ,
визначену за допомогою інтеграла
Лапласа (
,
визначену за допомогою інтеграла
Лапласа (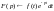 )
називається оператором або перетворенням
Лапласа.
)
називається оператором або перетворенням
Лапласа.
Теорема
проіснування зображення. Для всякого
оригіналу
 зображення
зображення
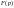 існує
в півплощині
існує
в півплощині
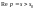 ,
де
,
де
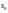 -показник
росту функції
-показник
росту функції
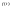 ,
причому ф-я
,
причому ф-я
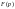 є
аналітична в цій півплощині (
є
аналітична в цій півплощині ( )
)
Доведення
першої частини теореми. Нехай
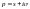 довільна
точка півплощини
довільна
точка півплощини
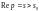 .
.
Враховуючи
що
 знаходимо:
знаходимо:
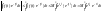 =
=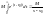 ,
,
Так
як
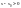 і
і
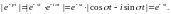 Таким
чином
Таким
чином
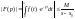 .
Звідси випливає абс. Збіжність інтегралу
.
Звідси випливає абс. Збіжність інтегралу
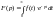 ,
тобто зображення
існує
і однозначне в півплощині
,
тобто зображення
існує
і однозначне в півплощині
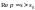 .
.
Необхідна
умова існування зображення. Якщо ф-я
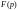 являє
собою зображення ф-ї
являє
собою зображення ф-ї
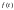 ,
то
,
то
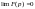 при
при
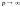 .
Це твердження витікає безпосередньо
з нерівності
,
коли
.
Це твердження витікає безпосередньо
з нерівності
,
коли
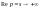 .
Так як
.
Так як
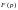 -аналітична
ф-я в півплощині
-аналітична
ф-я в півплощині
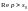 ,
то
,
то
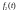 при
при
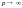 по любому напрямку.
по любому напрямку.
24 Властивості перетворення Лапласа
лінійність:
нехай
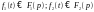 ,
тоді
,
тоді
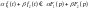 - випливає з лінійності інтеграла
- випливає з лінійності інтеграла
подібність:
нехай
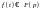 ,
тоді
,
тоді
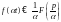
Доведення:
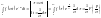
25. Властивості перетворення Лапласа
диференціювання
оригіналу:
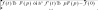
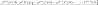
Доведення:
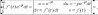

диференціювання
зображення:
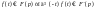
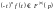
Доведення:

26. Властивості перетворення Лапласа
інтегрування
оригіналу:
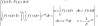
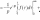
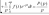
інтегрування
зображення:
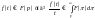 - випливає з властивості диференціювання
зображення.
- випливає з властивості диференціювання
зображення.
27.Властивості перетворення Лапласа
зсуву:
нехай
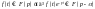
Доведення:
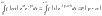
запізнення:
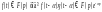
Доведення:
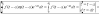
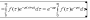
28. Теорема Бореля. Згортка функцій. Зображення згортки.
Теорема Бореля: Зображення згортки оригіналів дорівнює добутку їх зображень.

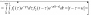
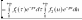
Інтеграл
вигляду
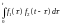 називають згорткою функцій
називають згорткою функцій
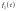 та
та
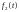 і позначають
і позначають
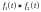 .
Зображення згортки ф-й відповідно до
теор. Бореля:
.
Зображення згортки ф-й відповідно до
теор. Бореля:
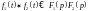
Згортка ф-й має властивість комутативності та асоціативності.
29 Інтеграл Дюамеля. Зображення періодичного сигналу.
Якщо
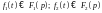 ,
то оригінал зображення
,
то оригінал зображення
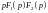 має вигляд
має вигляд
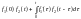 - формула (інтеграл) Дюамеля.
- формула (інтеграл) Дюамеля.
Доведення:
Спираючись на теорему про диференціювання
зображення отримаємо:
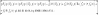

В результаті маємо два інтеграли Дюамеля:
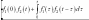
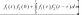
Нехай
оригінал
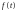 є ф-я періодична з періодом
є ф-я періодична з періодом
 .
Тоді
.
Тоді
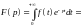
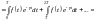
Позначимо
інтеграл
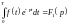 і зауважимо, що
і зауважимо, що
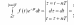 .
.
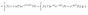
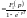
30. Формула Рімана-Мелліна
Якщо
ф-я F(p) - зображення ф-ї-оригіналу f(t), то
f(t) може бути знайдена за формулою
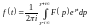
Ця
рівність має місце в кожній точці, в
якій f(t) неперервна. В точках разриву
ф-ї f(t) значення правої частини рівне :
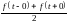
Інтеграл
в правій частині формули називають
інтегралом Мелліна; інтегрування може
проводитись по любій вертикальній
прямій p = σ + i ω, σ = const > σ0, − ∞ < ω <
∞, і інтеграл розуміється в смислі
головного значення:
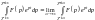 .
.
Оригінали |
Зображення |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|