
- •1 Поняття про числовий ряд і його суму.Необхідна умова збіжності ряду. Гармонічний ряд. Залишок ряду. Властивості збіжних рядів
- •2 Ознаки збіжності числових рядів з додатними членами
- •3. Ознака д’Аламбера. Радикальна та Інтегральна ознаки Коші.
- •4 Знакозмінні ряди. Ознака Лейбніца.
- •5 Знакозмінні ряди. Абсолютно і умовно збіжні ряди, їх властивості.
- •6 Функціональні ряди.
- •7 Властивості рівномірно збіжних рядів
- •8 Степеневі ряди. Властивості степеневих рядів.
- •9. Ряд Тецлора і Маклорен
- •10. Умови Дірихле розкладу ф-ції в ряд Фурє. Ряд Фур’є для парних і непарних ф-й.
- •11. Умови Дірихле розкладу ф-ції в ряд Фурє. Ряд Фур’є для ф-ї періоду
- •12 Інтеграл Фур’є для парних і непарних ф-й. Синус і косинус перетворення Фур’є.
- •13,14 Функція комплексної змінної. Границя. Неперервність. Основні елементарні ф-ї кз:
- •17 Диференціювання ф-ї комплексної змінної (фкз). Умови Коші-Рімана
- •18. Теорема Коші для однозв’язної області Теорема Коші для багатозв’язної області
- •20. Класифікація ізольованих особливих точок ф-ї.
- •21 Ряд Лорана. Теорема про розвинення ф-ї в кільці.
- •22. Означення лишку аналітичної функції в ізольованій особливій точці. Обчислення лишків в особливих точках.
- •23 Означення функції-оригіналу. Означення перетворення Лапласа. Теорема існування. Необхідна умова існування зображення.
17 Диференціювання ф-ї комплексної змінної (фкз). Умови Коші-Рімана
ФКЗ
 називається диференційовною в точці
називається диференційовною в точці
 ,
якщо вона визначена в цій точці та
деякому її околі і має місце рівність:
,
якщо вона визначена в цій точці та
деякому її околі і має місце рівність:
 ,
,
 .
Похідною ф-ї
.
Похідною ф-ї
 називається:
називається:
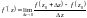 .
.
існування скінченої похідної ф-ї в точці рівносильне її диференційовності;
якщо ф-я диференційовна, то вона неперервна в точці, проте не напаки;
Теор.:
Для того, щоб ф-я
 була диференційовною в точці
була диференційовною в точці
 необхідно і достатньо виконання
наступних умов:
необхідно і достатньо виконання
наступних умов:
ф-ї
 та
та
 повинні бути неперервно диференційовними
в точці
повинні бути неперервно диференційовними
в точці
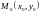
Справедливі
умови Коші-Рімана:

Доведення:
Покладемо





Тепер
покладемо





18. Теорема Коші для однозв’язної області Теорема Коші для багатозв’язної області
Якщо
ф-я
 аналітична
в однозв’язній обл.
аналітична
в однозв’язній обл.
 ,
то інтеграл від цієї ф-ї по будь-якому
замкнутому контуру
,
то інтеграл від цієї ф-ї по будь-якому
замкнутому контуру
 ,
що лежить обл.
,
що лежить обл.
 ,
рівний нулю
,
рівний нулю
 .
.
Доведення:
Припустимо що похідна
 неперервна. Маємо
неперервна. Маємо
 .
В силу аналітичності
.
В силу аналітичності
 і неперервності
і неперервності
 в однозв’язній обл.
в однозв’язній обл.
 ,
то ф-ї
,
то ф-ї
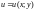 і
і
 неперервні і диференційовні в цій обл.
і задовольняють умовам Коші-Рімана:
неперервні і диференційовні в цій обл.
і задовольняють умовам Коші-Рімана: ,
,
 .
Ці умови означають рівність нулю
інтегралів
.
Ці умови означають рівність нулю
інтегралів
 і
і
 .
Звідси слідує, що
.
Звідси слідує, що
 .
.
Р озглянемо
на прикладі 3-звязної обл.
,
що обмежена зовнішнім контуром
озглянемо
на прикладі 3-звязної обл.
,
що обмежена зовнішнім контуром
 і внутр. контурами
і внутр. контурами
 та
та
 .
Проведемо 2 розрізи
.
Проведемо 2 розрізи
 і
і
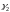 області
області
 ,
отримаємо однозв’язну обл.
,
отримаємо однозв’язну обл.
 ,
обмежену замкнутим контуром
,
обмежену замкнутим контуром
 ,
що складається з контурів
,
що складається з контурів
 ,
, ,
, і розрізів
і розрізів
 та
та
 :
:
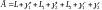 .
По теоремі Коші для однозв’язної обл.
.
По теоремі Коші для однозв’язної обл.
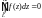 ,
але
,
але
 ,
так як кожний із розрізів
,
так як кожний із розрізів
 і
і
 при інтегруванні проходиться двічі
різними напрямами. Тому отримуємо
при інтегруванні проходиться двічі
різними напрямами. Тому отримуємо
 ,
тобто інтеграл від аналітичної в
замкнутій області ф-ї
,
тобто інтеграл від аналітичної в
замкнутій області ф-ї
 по границі області
,
що проходиться в додатному напрямку,
рівний нулю.
по границі області
,
що проходиться в додатному напрямку,
рівний нулю.
20. Класифікація ізольованих особливих точок ф-ї.
Якщо
ф-я
 аналітична в крузі з виколотим центром
аналітична в крузі з виколотим центром
 і неаналітична в точці
і неаналітична в точці
 ,
то така точка називається ізольованою
особливою точкою цієї ф-ї.
,
то така точка називається ізольованою
особливою точкою цієї ф-ї.
Ізольована
особлива точка ф-ї
 називається усувною особливою точкою,
якщо ряд Лорана в області
для такої ф-ї не містить від’ємних
степенів.
називається усувною особливою точкою,
якщо ряд Лорана в області
для такої ф-ї не містить від’ємних
степенів.
Ізольована
особлива точка ф-ї
називається полюсом n-го порядку, якщо
ряд Лорана для цієї функції в області
 містить скінчену кількість від’ємних
степенів найвищим з яких є
містить скінчену кількість від’ємних
степенів найвищим з яких є
 .
.
Ізольована
особлива точка ф-ї
називається істотно особливою, якщо
ряд Лорана для цієї ф-ї в області
 містить нескінченну кількість від’ємних
степенів.
містить нескінченну кількість від’ємних
степенів.
