Логопериодические антенны. Особенности и конструкции, входное сопротивление, дн.

П ринцип автоматической отсечки излучающих токов воплощен также в антеннах с логарифмической периодичностью параметров в зависимости от частоты, для краткости называемых просто логопериодическими антеннами. Плечами антенны являются своеобразные структуры из взаимно чередующихся вибраторов в форме выступов и впадин. Геометрия структур характеризуется безразмерным периодом =R_n/R_n+1, коэффициентом формы =r_n/R_n и углами  и .

Обычно используются структуры с параметром = . Плечи антенны вначале координат разделены зазором. Возбуждающий кабель припаивается оплеткой к одному плечу антенны на всем его протяжении, внутренний проводник кабеля присоединяется к началу другого плеча антенны.

Электрический ток в выступах структуры при удалении от центра возрастает, достигая максимума в месте расположения резонансных выступов примерно четверть волновой длины. Направления наиболее интенсивных токов, определяющих излучения антенны, показаны стрелками на рисунке.

После прохождения резонансных выступов токи резко уменьшаются, т.е. происходит их отсечка. С уменьшением частоты излучаемых колебаний последовательно возникают резонансы выступов, более удаленных от центра. Отношение двух частот на которых резонируют соседние выступы составляет в точности величину =₁/₂. Поэтому входное сопротивление и ДН антенны оказываются периодическими функциями логарифма частоты колебаний. При правильном подборе параметров структуры изменения характеристик антенны в пределах одного периода оказывается небольшим.

Среднее входное сопротивление плоской логопериодической антенны обычно превышает 100 Ом и зависит от значения углов  и . При ==45 форма металлической части антенны совпадает с формой ее щелевой дополнительной части и в соответствии с формулой Z₁Z₂=(60)² входное сопротивление должно составлять около 188 Ом. Уменьшение среднего входного сопротивления, желательно для облегчения согласования входа антенны с 75-омным коаксиальным кабелем, может быть достигнуто уменьшением угла .

Д Н плоской логопериодической антенны состоит из двух широких лепестков, ориентированных перпендикулярно плоскости плеч. Излучение в плоскости антенны невелико для всех направлений. Вектор Е в направлении максимального излучения поляризован параллельно оси х, а излучение с поляризацией параллельной оси у, мало. Ширина лепестков ДН зависит от безразмерного периода структуры . При изменении  от 0,80 до 0,25 при углах ==45 происходит плавное уменьшение ширины лепестков по половинной мощности от 73 до 38.

Апертурные антенны: рупорные антенны. Линзовые антенны: диэлектрическая линза, линзы Люнеберга, металлопластинчатые линзы с повышенной фазовой скоростью.

К апертурным относят антенны, у которых в соответствии с принципом эквивалентности, может быть выделена плоская поверхность раскрыва S, формирующая остронаправленное излучение. Наиболее распространены зеркальные (в частности, параболические), а также рупорные и линзовые апертурные антенны. КНД апертурных антенн связан с площадью раскрыва S и длиной волны  общей формулой:

,

где 1 – общий (результирующий) коэффициент использования поверхности (КИП), зависящий от вида амплитудно-фазового распределения возбуждения и других факторов. Ширина луча по уровню -3 дБ апертурной антенны в какой либо плоскости, перпендикулярной поверхности раскрыва обратно пропорциональна линейному размеру раскрыва L в этой плоскости:

,

где 1- коэффициент расширения луча, зависящий от формы раскрыва и вида амплитудно-фазового распределения возбуждения.

На дециметровых и более коротких волнах широкое применение находят рупорные антенны и, в частности антенны в виде открытого конца прямоугольного или круглого волновода. Рассмотрим излучатель в виде открытого конца прямоугольного волновода.

Р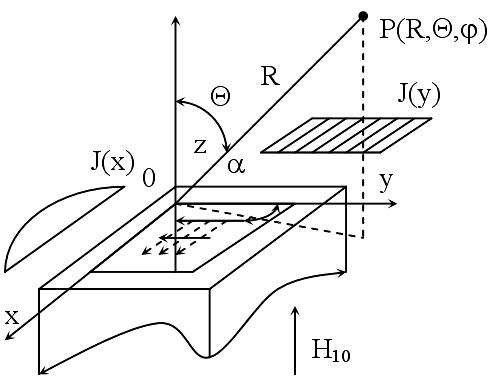 аспространяющаяся в волноводе основная волна Н₁₀ дойдя до его открытого конца частично излучается и частично отражается обратно к генератору. В месте перехода от волновода к открытому пространству т.е. в раскрыве, возникают волны высших типов, а также появляются поверхностные токи на наружных поверхностях стенок волновода. Для поля излучения прямоугольного волновода строго решения не найдено. В инженерных расчетах предполагают, что касательные составляющие поля в раскрыве волновода (а следовательно, и эквивалентные электрические и магнитные токи) представляют сумму падающей и отраженной волн основного типа колебаний:

,

,

где -коэффициент отражения от открытого конца волновода Z_C= .

В прямоугольном волноводе с соотношением сторон b/a = 0,45 коэффициент отражения составляет 0,3-0,2 и имеют фазу /3-/2. Причем первые цифры относятся к нижней рабочей частоте волновода, вторые к верхней. Дн открытого конца волновода в передней полусфере в плоскостях уОz (плоскость Е) и хОz (плоскость Н) с хорошей степенью точности определяется формулами:

,

.

Здесь а и b -внутренние размеры волновода,

– отношение длины волны в свободном пространстве к длине волны Н₁₀ в прямоугольном волноводе.

Угол  отсчитывается от оси z.

.

Н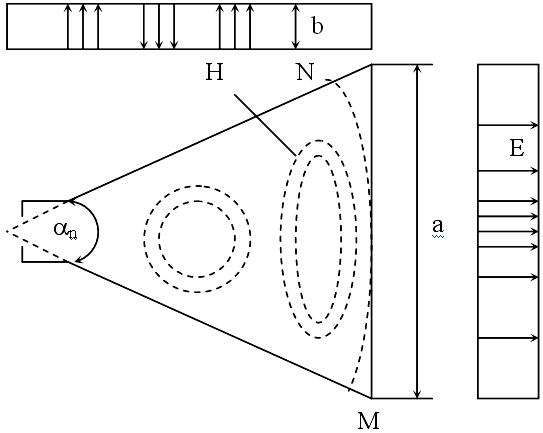 -секториальный рупор расширяющийся в плоскости вектора Н. В рупоре возникает волна, подобная волне Н₁₀ в прямоугольном волноводе. Однако секториальный рупор отличается от волновода тем, что в нем фронт волны образует цилиндрическую поверхность, фазовая скорость является переменной величиной, зависящей от отношения а/, поле на большом расстоянии от горловины рупора принимает вид чисто поперечной волны. Фазовая скорость приближенно определяется формулой

и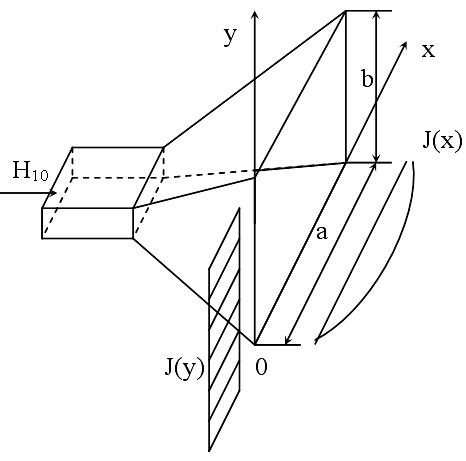 вблизи раскрыва рупора приближаются к скорости света, что приводит к уменьшению отражения волны от излучающей поверхности раскрыва.

КНД рупорной антенны при фиксированной длине рупора имеет характерную зависимость от размера раскрыва а/. Наличие максимума объясняется тем, что при увеличении угла раствора рупора, с одной стороны, увеличивается относительный размер раскрыва а/, что ведет к сужению ДН, с другой согласно формуле

Ф₂=-(2/)МN-а²/(4R)=-[a/(2)]tg(_н/2) (1)

быстро увеличивается квадратичная фазовая ошибка |Ф₂|, ведущая к расширению ДН.

В результате действия двух этих факторов при определенном электрическом размере раскрыва имеет место максимальный КНД. Оказывается, что при любой длине рупора максимум КНД получается при квадратичной фазовой ошибке на краю рупора, равной 135. Н-секториальный рупор, удовлетворяющий этому условию, принято называть оптимальным. Полный КИП оптимального Н-секториального рупора равен примерно 0,64 (0,81-апертурный КИП, обусловленный спадающим до 0 на краях раскрыва амплитудным распределением; 0,79 - КИП, обусловленный квадратичной фазовой ошибкой).

Е-секториальный рупор расширяется в плоскости вектора Е. Ширина ДН в плоскости Н Е-секториального рупора такая же и как у открытого конца волновода, а в плоскости Е ширина луча с увеличением размера b уменьшается, если угол раствора _Е взят достаточно малым. В Е-секториальном рупоре амплитудное распределение поля в раскрыве приблизительно равномерное и квадратичная фазовая ошибка Ф₂-b²/(4R) на краю раскрыва, соответствующая оптимальному рупору с наибольшим КНД составляет 90.

Широко применяются пирамидальные рупоры с прямоугольным поперечным сечением они позволяют сужать ДН как в плоскости Н так и в плоскости Е. В пирамидальном рупоре образуется сферическая волна фазовая скорость которой является переменной и у открытого конца приближается к скорости света. Вследствие этого отражение волны от раскрыва незначительно - рупор согласовывает волновод с открытым пространством. Фазовые искажения поля в раскрыве могут быть определены по формуле (1) в плоскости Н и по аналогичной формуле (при замене а на b) в плоскости Е.

Достоинствами рупорных антенн являются простота и неплохие диапазонные свойства. Все оптимальные и более длинные рупоры могут быть использованы во всей рабочей полосе частот питающего волновода. Самостоятельные рупорные антенны чаще всего применяются в измерительных установках например как эталонные антенны с известным коэффициентом усиления. Кроме того, рупоры широко используются для облучения зеркальных и линзовых антенн, а также в конструкциях антенн других типов, например импедансных.

Линзовые антенны.

В линзовых антеннах используются оптические свойства электромагнитных волн, поскольку размеры и радиусы кривизны поверхности линзовых антенн обычно много больше длины волны. Для антенн линз характерно, то, что в них цилиндрический или сферический фронт волны преобразуется в плоский.

Н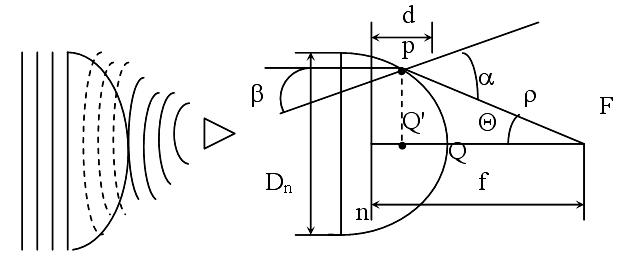 а рисунке показана диэлектрическая линза, на которую от источника F (облучателя) падает сферическая волна.

Преломляясь на выпуклой освещенной поверхности линзы, сферический фронт волны преобразуется в ней в плоский при одновременном укорочении длины волны в диэлектрике . Выходная поверхность линзы является плоской, и по выходу из нее фронт волны остается плоским. Поскольку размеры выходной поверхности линзы велики по сравнению с длиной волны, излучение ее оказывается остронаправленным.

Определим форму профиля линзы. Пусть луч из точки F падает в точку Р поверхности линзы и характеризуется углом падения  и углом преломления . Эти углы определяются по отношению к местной нормали к освещенной поверхности линзы. На основании закона преломления лучей

sin=nsin,

где - коэффициент преломления диэлектрика.

Уравнение профиля линзы можно найти из условия постоянства длины оптического пути (электрической длины) от преобразуемой к преобразованной поверхности равных фаз по любому направлению, т.е. FР=FQ+nQQ'. Отсюда получаем =f+n(cos-f) или

=(n-1)f/(ncos-1) (1),

где f-фокусное расстояние, т.е. расстояние от фокуса F до вершины линзы Q; -угол между осью линзы и лучом; -расстояние от фокуса до текущей точки поверхности линзы.

Уравнение (1) представляет собой уравнение гиперболы. Таким образом, выпуклая поверхность диэлектрической линзы должна иметь гиперболическую форму. Толщина линзы d определяется по оптическрму пути и связана с её диаметром D_Л соотношением

, (2)

где _max - угол между осью линзы и направлением из фокуса в крайнюю точку профиля.

Угол 2_max , под которым из фокуса видны края линзы, часто называют углом раскрыва линзы. Формулы (1) и (2) позволяют рассчитать профиль и найти геометрические размеры линзы.

Диэлектрические линзы являются широкополосными, если коэффициент преломления не зависит от частоты на сантиметровых волнах эти линзы применяются редко из-за большой массы и трудности изготовления и трудности изготовления.

Линзы Люнеберга. Среди линзовых антенн уникальными свойствами обладают линзы из неоднородного диэлектрика со сферической симметрией, называемые по имени автора линзами Люнеберга. Установлено, что если показатель преломления в сферической линзе изменяется вдоль радиуса по закону :

(1),

где R_max – радиус сферы, R – текущий радиус точки внутри сферы,

то такая линза превращает сферический фронт волны точечного источника I, расположенного на поверхности сферы , в плоский фронт волны.

П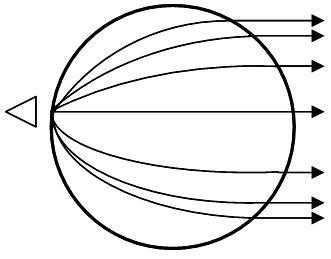 еремещая первичный источник (например, открытый конец волновода или рупор) по поверхности сферы, можно перемещать луч антенны по всем направлениям без искажений формы ДН. Однако чаще сферическую линзу Люнеберга снабжают решеткой облучателей, каждому из которых соответствует своя неподвижная остронаправленная ДН. Возникает так называемая многолучевая антенная система, способная обслуживать одновременно и независимо несколько передатчиков или приемников. Возможно осуществлять непрерывный радиолокационный контроль окружающей обстановки в широком секторе углов, а также вести направленную радиосвязь с многими корреспондентами.

В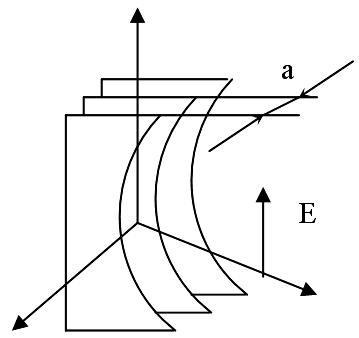 конструктивном отношении линза Люнеберга может представлять собой набор однородных концентрических слоев и радиочастотной пенокерамики, причем плотность слоев должна уменьшатся от центра к периферии, чтобы обеспечить аппроксимацию закона изменения показателя преломления (1). Наряду со сферическими существуют и цилиндрические линзы Люнеберга, допускающие неискаженное перемещение луча только в одной плоскости.

Металлопластинчатые линзы.

Чаще всего применяются металлопластинчатые линзы с повышенной фазовой скоростью. Такие линзы выполняются из параллельных металлических пластин расположенных на расстоянии а одна от другой и образующих вогнутую поверхность. Вектор напряженности электрического поля Е, возбуждаемого облучателем расположенным в фокусе линзы, должен быть параллелен пластинам.

Т огда пространство между двумя соседними пластинами представляет волновод, в котором распространяется волна типа Н₁₀ с фазовой скоростью . Т.О., возникает среда с эффективным коэффициентом преломления.

(1).

Расстояние между пластинами а должно удовлетворять неравенствам /2 <a<, для того чтобы между пластинами могла распространятся только волна типа Н₁₀. Следовательно, коэффициент преломления ускоряющей линзы находится в пределах 0<n< .

Уравнение профиля линзы можно получить с помощью построений, показанных на рисунке. Луч, падающий из фокуса F в точку р освещенной поверхности линзы, преломляется по закону геометрической оптики sin=nsin. Оптическая длина пути FQ должна быть равна оптической длине пути FP', т.е. FQ=FP+nPP'. Это условие приводит к формуле =(n-1)f/(ncos-1) для профиля линзы, однако, при n<1 формула представляет уравнение эллипса. Толщина профиля линзы дается формулой ,

где 2_max - угол раскрыва линзы; D_л-размер раскрыва.

Ускоряющая линза собранная из профилированных по эллипсу одинаковых пластин, фокусирует излучение в плоскости вектора Е. Если же ускоряющая линза собрана из прямоугольных пластин разной толщины d так, что они также образуют эллиптический профиль, то она фокусирует излучение в плоскости вектора Н. В этом случае на освещенной поверхности линзы угол преломления луча не зависит от коэффициента преломления n и направление преломленных лучей при любом n задается направлением волноводных каналов между пластинами. Линзы с таким свойством называются линзами с принудительным направлением распространения. Для фокусировки излучения одновременно в плоскостях Е и Н линза должна быть собрана из профилированных пластин разной толщины.

Металлопластинчатые линзы небольших и средних размеров конструктивно очень просты. Металлопластинчатые линзы сравнительно узкополосны, так как коэффициент преломления согласно формуле (1), зависит от длины волны. Расчеты показывают, что если принять коэффициент преломления на средней частоте равным 0,5 и допустить квадратичные фазовые искажения на крайних частотах, то рабочая полоса частот (в %) 2f/f₀=33₀/d.

Зеркальные параболические антенны. Конструкции антенн, выбор параметров параболической антенны. Точность изготовления зеркала, виды облучателей. Двухзеркальная антенна Кассегрена, двухзеркальная антенна Грегори, квазипараболическая двухзеркальная антенна.

Зеркальные параболические антенны являются наиболее распространенными остронаправленными антеннами. Их широкое применение в самых разнообразных радиосистемах объясняется простотой конструкции, возможностью получения разнообразных видов ДН, высоким КПД, малой шумовой температурой, хорошими диапазонными свойствами и т.д.

К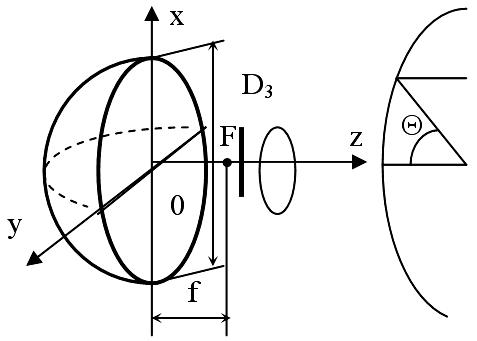 лассическими являются параболические антенны, которые могут выполняться в виде параболоида вращения, параболического цилиндра или закрытой конструкции, ограниченной параллельными проводящими плоскостями.

Параболоид вращения возбуждается слабонаправленным облучателем (например, рупором), помещенным в фокусе зеркала, и преобразует сферический фронт волны в плоский. В этих антеннах так же как и в линзах, используются оптические свойства радиоволн. Геометрические свойства параболы таковы, что лучи, направляемые из фокуса и отражаемые от параболы, становятся параллельными её оси. Длина пути от фокуса до параболы и затем до линии раскрыва, проходящей через края параболы, одинакова для любого угла .

Таким образом, в раскрыве параболической антенны образуется синфазная поверхность, и излучение антенны становится остронаправленным. В декартовой системе координат параболоид вращения определяется уравнением (начало координат совпадает с вершиной параболоида) х²+у²=4fz, а в сферической системе координат (начало координат совпадает с фокусом параболоида) - уравнением ()=2f/(1+cos).

Различают длиннофокусные и коротко фокусные параболические антенны. В длиннофокусной антенне фокус находится вне антенны f>D_a/4 и угол раскрыва 2_MAX, под которым зеркала видны из фокуса, удовлетворяет условию 2_MAX<. В короткофокусной антенне фокус находится внутри объема между зеркалом и его раскрывом, т.е. f<D_a/4 и 2_MAX<.

Для расчета излучения параболических антенн традиционно используется метод эквивалентных поверхностных электрических и магнитных токов. Применяются два способа записи интегралов излучения:

1) с интегрированием по поверхности плоского раскрыва и по теневой (тыльной) стороне параболоида;

2) с интегрированием по криволинейной поверхности, которая проходит по освещенной и теневой сторонам параболоида.

О выборе параметров параболической антенны. При расчете параболической антенны апертурным методом обычно предполагают, что ДН облучателя F() обладает симметрией вращения относительно оси зеркала. По известной ДН облучателя находят амплитудное распределение в раскрыве с помощью формул:

Здесь R-радиальная координата в плоскости раскрыва, -угол между осью параболоида и направлением из фокуса в текущую точку отражения на параболоиде. Найденное амплитудное распределение апроксимируется по формуле: т.е. находится подходящее значение показателя степени n и величины (1-) - уровня поля на краю раскрыва. Последующие вычисления по формуле

,

где  =  a sin – угловая переменна, и их анализ позволяют определить ширину луча антенны и уровень боковых лепестков. Аппертурный К_ипа, учитывающий неравномерность амплитудного распределения, определяют по формуле

или по таблице апертурных распределений из справочника.

Выполняя несложное интегрирование можно определить эффективность облучателя К_{ип обл}, т.е. долю его мощности излучения, попадающую на зеркало:

. (3)

Этой величиной учитывается бесполезная потеря мощности облучателя за счет "переливания" ее через края зеркала. Найденные значения параметров антенной системы оказываются зависящими от относительного фокусного расстояния f/D₃, т.е. от угла раскрыва зеркала 2_max. Существует оптимальное значение относительно фокусного расстояния (f/D₃)_opt, при котором достигается максимум результирующего КИП. Установлено, что f/D₃=0,38, уровень возбуждения на краю раскрыва в оптимальном случае составляет примерно 0,33 (или -10 дБ), результирующий КИП при этом равен 0,83.

Рассмотренный способ приближенного расчета применяется на этапе эскизного проектирования недорогих зеркальных антенн небольших размеров (D₃23 м на сантиметровых волнах). В этом случае небольшая потеря КИП из-за не оптимальности конструкции облучателя легко компенсируется некоторым увеличением размеров раскрыва. Однако стоимость изготовления зеркал больших размеров при возрастании диаметра очень быстро увеличивается. Поэтому для крупной зеркальной антенны вопрос получения максимального КИП приобретает особую важность. В этом случае оптимизация всей конструкции зеркальной антенны и ее облучателя должна производится на основании более точных расчетов с учетом возможно большего числа факторов.

Наиболее важные факторы, влияющие на общий КИП зеркальной антенны:

1. Вид амплитудного распределения в раскрыве и соответствующий К_{ип а};

2. Эффективность облучателя К_{ип обл}, определяемая формулой (3)

3. Затенение части поверхности раскрыва облучателем и поддерживающими его конструкциями;

4. Ответвление электрических токов на теневую поверхность зеркала, приводящее к росту дальних боковых лепестков.

5. Появление кроссполяризации, учитываемой отдельным множителем К_{ип м}.

6. Фазовые ошибки распределения эквивалентных поверхностных токов в раскрыве (систематические и случайные);

7. Омические потери мощности из-за конечной проводимости отражающих поверхностей, наличия неидеальных диэлектриков, антикоррозионных покрытий и т.д.;

8. Влияния радиопрозрачного укрытия антенны (если оно используется), создающего дополнительные фазовые ошибки в распределении токов в эквивалентном раскрыве.

Виды облучателей. Вибраторные облучатели. Состоят из активного вибратора и контррефлектора в виде диска или пассивного вибратора. Для питания активного вибратора может использоватся коаксиальная линия или прямоугольный волновод. Ширина луча оказывается одинаковой в плоскостях Е и Н и составляет примерно 130 по уровню -10 дБ. Облучатель обеспечивает К_ИП0,65 и способен работать в полосе частот около 12% при КСВ не более 1,5.

Щелевой облучатель. При небольших мощностях излучения на сантиметровых волнах удобен двухщелевой облучатель Катлера. Изогнутая форма и взаимное расположение щелей прорезанных в ближнем к зеркалу торце цилиндрического резонатора, а также диаметр круглого экрана подбираются таким образом, чтобы получить одинаковую ширину ДН в плоскостях Е и Н (около 130) по уровню поля -10 дБ. Для согласования облучателя используют плавный переход за счет сужения узких стенок волновода и настроечный штырь, ввертываемый в дальнюю от зеркала торцовую стенку резонатора. Облучатель позволяет получить аппертурный КИП зеркала примерно 0,57 (с учетом потерь на "переливание" мощности). Недостатком облучателя Катлера является узкая полоса рабочих частот (около 3%).

Волноводные и рупорные облучатели. Просты по конструкции, широкополосны и позволяют в широких пределах подбирать нужную ширину ДН. Обычно волноводные или рупорные облучатели с рабочим типом волны Н₁₀ в прямоугольном и Н₁₁ в круглом волноводе в настоящее время применяются редко, так как не обеспечивают осевой симметрии ДН, а искривленность силовых линий электрического и магнитного полей в их раскрыве приводит к возникновению значительных кроссополяризационных составляющих поля излучения. Наиболее совершенными в настоящее время считаются рупорные волноводные излучатели с внутренней гофрированной поверхностью.

Линейные облучатели. Для зеркальных антенн в виде параболических цилиндров требуются облучатели линейных антенн с длиной, равной длине образующей зеркала. В плоскости xOz ДН таких облучателей должны обеспечивать необходимое амплитудное распределение в раскрыве параболического цилиндра. Кроме того, в раскрыве облучателя должно формироваться специальное амплитудно-фазовое распределение возбуждения вдоль оси У, обеспечивающее требуемую форму ДН всей антенны в плоскости yOz. В качестве линейных облучателей могут использоваться волноводные многощелевые решетки, секториальные рупоры, микро полосковые линейные решетки и др.

Двухзеркальная антенна Кассегрена. В этой антенне для получения синфазного распределения поля в раскрыве, используются две отражающие поверхности: вогнутое главное (большое) параболическое зеркало 1 и выпуклое вспомогательное (малое) зеркало 2, в виде гиперболоида вращения. Один из фокусов F₁ вспомогательного гиперболического зеркала совмещается с фокусом главного зеркала. Во втором фокусе F₂ находится фазовый центр облучателя 3, и вследствие этого лучи, отраженные от зеркала 2, можно рассматривать как идущие из расположенного за ним "виртуального облучателя" 4 в точке F₁. Изображение виртуального облучателя строится по правилам геометрической оптики и оказывается уменьшенным.

Д

1

2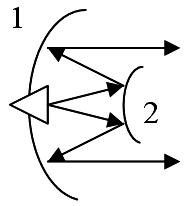

вухзеркальная антенна Кассегрена отличается от однозеркальной рядом положительных качеств. Она дает возможность укоротить тракт СВЧ и разместить основную часть конструкции облучателя за зеркалом, что особенно удобно в моноимпульсных радиолокаторах. Уменьшение фокусного расстояния главного зеракала, а также малое расстояние поля облучателя в заданную полусферу главного зеркала способствуют уменьшению шумовой температуры. Недостатками двухзеркальной антенны являются обратная реакция малого зеркала на облучатель и увеличенное затенение раскрыва по сравнению с однозеркальной антенной.

Д вухзеркальная антенна Грегори. Здесь используется два вогнутых зеркала: главное зеркало с параболической формой поверхности и вспомогательное с эллептической поверхности. Один из фокусов вспомогательного эллептического зеркала F₁ совмещается с фокусом главного зеркала. Во второй фокус эллипса F₂ помещается фазовый центр облучателя. Волны от облучателя попадают на вспомогательное зеркало, фокусируются им в точке F₁ и следуют далее на главное зеркало, создавая синфазный фронт волны в его раскрыве.

Как показывают теоретические и экспериментальные исследования, общий КИП двухзеркальной антенны Грегори получается несколько выше, чем в антенне Кассегрена, и схему Грегори предпочитают при строительстве крупных полноповоротных антенн.

Квазипараболические двухзеркальные антенны. Классические параболическая и эллиптическая формы главного и вспомогательного рефлекторов двухзеркальной антенны Грегори могут быть модифицированы таким образом, чтобы при сохранении синфазности поля в раскрыве главного зеркала, улучшить равномерность амплитудного распределения, и тем самым увеличить общий КИП антенны. Следует обратить внимание на отсутствие общей точки пересечения лучей после отражения от малого зеркала, а также на сгущение лучей к краям раскрыва основного зеркала, вызывающее подъем амплитудного распределения на краях.

67