Многощелевые волноводные антенны. Антенны с синфазным возбуждением щелей. Несинфазные многощелевые волноводные антенны. Конструкции, основные характеристики.

Для получения узких диаграмм направленности и соответственно повышения КНД используются антенны на базе прямоугольного волновода состоящих из многих щелей. Одним из вариантов является много щелевая антенна с синфазным возбуждением щелей. Представляет собой конструкцию из закороченного волновода, у которого в широкой стенке сделаны продольные щели в шахматном порядке.

Р 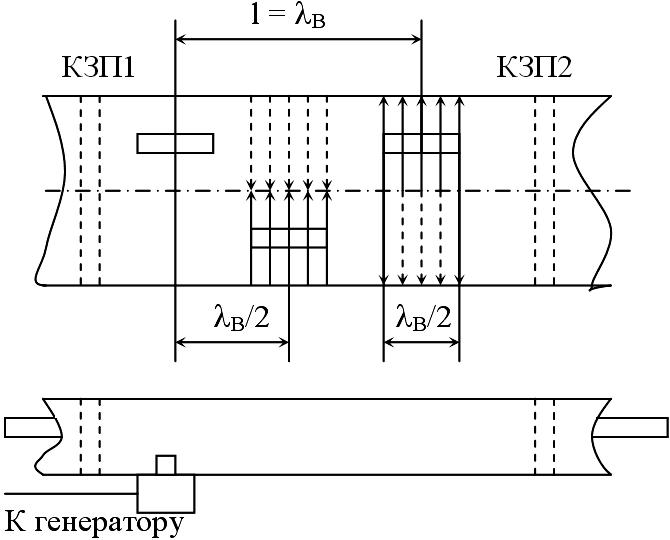асположение щелей на расстоянии _В в одном ряду обеспечивает их синфазное возбуждение. Во втором ряду щели смещены относительно первого ряда на расстояние _В/2 и они также возбуждаются синфазно по отношению к первому ряду. При выполнении антенны из поперечных щелей, при расположении щели на расстоянии _В происходит рост боковых лепестков, поэтому такие антенны менее распространены.

КЗ поршни (КЗП) используются для настройки соответственно коаксиально-волнового перехода, максимум стоячей волны должен приходится на место положения зонда. КЗП2 используют для настройки возбуждения щелей, излучение на них будет максимальное, если максимальная густота силовых линий попадает в центр щели.

Характеристика направленности такой антенны может быть рассчитана по формуле:

,

где n – число щелей,

d – расстояние между центрами соседних щелей (вдоль оси х);

 - угол между нормами к широкой стенке волновода и направлением на точку наблюдения;

=2/ - коэффициент фазы.

КНД в плоскости вектора Е (xOy) может быть определен выражением

D =3,2 .

Удовлетворительное согласование получается в узкой полосе частот, в связи с привязкой размеров к длине волны.

При условии, что расстояние между щелями

Несинфазные многощелевые волноводные антенны.

Для получения узких диаграмм направленности и соответственно повышения КНД используются антенны на базе прямоугольного волновода состоящих из многих щелей. Одним из вариантов является многощелевая антенна с несинфазным возбуждением щелей. Представляет собой конструкцию из закороченного волновода, у которого в широкой стенке сделаны продольные щели в шахматном порядке.

Р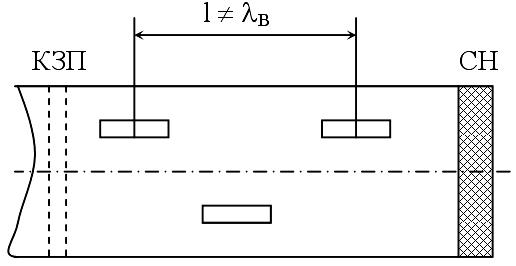 асположение щелей на расстоянии несколько отличном от _В в одном ряду обеспечивает их несинфазное возбуждение. Соседние щели в этом случае возбуждаются с небольшой разностью фаз. Волна, отраженная от конца волновода, полностью поглощается согласованной нагрузкой (СН).

Со стороны зондового перехода имеется коротко замыкающий поршень (КЗП), а с другого конца волновода согласованная нагрузка.

КЗ поршень используется для настройки возбуждения щелей, излучение на них будет максимальное, если максимальная густота силовых линий попадает в центр щели.

Фазы токов возбуждающих щели изменяются вдоль антенны по линейному закону, что приводит к изменению направления максимального излучения.

Полосковые и микрополосковые антенны. Конструкции, достоинства и недостатки антенны. Распределение магнитных токов. Диаграмма направленности в плоскости е и н.

П олосковые и микрополосковые антенны выполняют по интегральной технологии, как и другие устройства СВЧ (делители мощности, фазовращатели, согласующие элементы). К достоинствам этого вида антенн относятся простота, сравнительно небольшие объем и масса, низкопрофильность, т.е. малое аэродинамическое сопротивление при размещении на поверхности летающих объектов.

Составными частями простейшего полоскового излучателя (см. рис.) являются металлическая пластина 1, экран 3 и диэлектрическое основание 2 (подложка). Форма металлических пластин-излучателей весьма разнообразна. Наиболее распространены пластины прямоугольной, круглой и эллиптической формы. Возбуждение пластин может осуществляться либо коаксиальной линией через отверстие в экране и подложке, либо полосковой линией в плоскости пластины. В качестве диэлектрического основания обычно используются диэлектрики с параметрами: _r2,510,0 и tg10^-4-10^-3. Толщина основания h может составлять (0,10,01).

Микрополосковые излучатели относятся к резонансным антеннам. Упрощенно можно считать, что объемный резонатор микрополоскового излучателя ограничен вертикальными стенками из идеального магнитопроводящего материала, расположенными по периметру пластины. В прямоугольных микрополосковых антеннах используется низший тип резонанса, при котором

L_В/2,

где ₀ - длина волны в полосковой линии передачи с шириной проводника /2.

Составляющая электрического поля в поперечном сечении плоской линии (вдоль координаты у) между пластиной и экраном распределена почти равномерно, а в продольном (вдоль координаты х) – по синусоидальному закону с пучностями на краях пластины. Заметные отклонения от такого идеализированного распределения наблюдаются только вблизи углов пластины и в окрестности точки питания.

Существенным недостатком одиночного микрополоскового излучателя является узкополосность, связанная с резонансным механизмом действия антенны.

Р аспределение магнитных токов и в эквивалентной щели, построенное исходя из картины распределения поля в резонаторе прямоугольной формы микрополосковой антенны. Главную роль в формировании излучаемого поля играют равномерно распределенные синфазные токи ₁ и ₃, создающие линейно поляризованное излучение с вектором Е, параллельным оси х. Токи ₂ и ₄ содержат на каждой боковой стороне пластины по два противофазных участка, излучение которых, в значительной степени взаимно компенсируется (точная компенсация имеет место в плоскостях zOx и zOy).

Можно получить следующие выражения для ДН прямоугольной микрополосковой антенны:

,

где ; ; .

В выражении для f_ первый член в скобках соответствует излучению двух торцевых щелей с равномерным распределением магнитного тока, второй член – излучению боковых щелей. Размер L должен определятся из условия резонанса L0,5₀ .

Характерный вид ДН прямоугольной микрополосковой антенны изображен на рисунке.

ДН микрополосковой антенны с прямоугольной пластиной в плоскости Е (а) и в плоскости Н (б)