6. Оценка точности результатов измерения с использованием информационных подходов

Носителями измерительной информации могут быть только такие сигналы, изменение которых во времени нельзя точно предсказать заранее. Любая зависимость, точно определяемая до поступления сигнала, не сообщает ничего нового – не несет информации. Количество информации зависит от степени неопределенности сигнала до его приема. Неопределенность уменьшается после приема измерительного сигнала (после измерения). Таким образом, мерой информации является степень устранения неопределенности, степень увеличения вероятности наступления какой-то возможности. Достоверность информации равнозначна вероятности Р=1, это значение исключает возможность ошибок, помех. Степень неопределенности, в свою очередь, определяется энтропией.

В соответствии с теорией информации [35] количество информации, получаемой при каком-либо измерении, равно

,

где - энтропия измеряемой величины до измерения,

- энтропия измеряемой величины с учетом доверительного интервала, энтропия погрешности.

Используя информационный подход, рассчитаем погрешность измерения, имеющую место при использовании измерительного прибора с диапазоном измерения от X­_1­ до X₂. Будем считать, что вероятность попадания результата до и после измерения распределена в соответствии с равновероятностным законом.

Дифференциальная функция распределения вероятности появления измеряемой величины до проведения измерения

Дифференциальная функция попадания результата измерения на определенный участок диапазона измерения измерительного прибора после измерения

где - результат измерения, - интервал неопределенности.

Энтропия дискретных случайных величин равна

случайная величина может рассматриваться как непрерывная, ее энтропия

Энтропия до и после проведения измерения в этом случае будет равна

Полученное за счет измерения количество информации

.

Величина N показывает, какое количество интервалов неопределенности шириной размещается в диапазоне измерений измерительного прибора.

Графическое изображение полученных результатов приведено на рис.3.

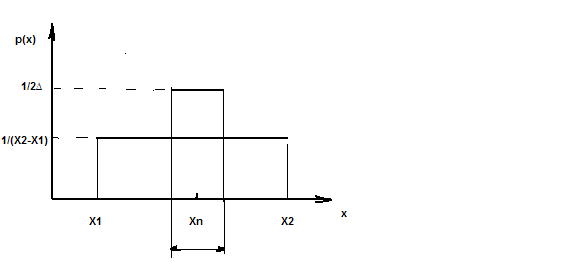Рис. 3. Дифференциальные функции распределения вероятности попадания измеряемой величины и результата ее измерения в определенный участок диапазона измерений измерительного прибора

Если вероятность попадания результата измерения после измерения распределена в соответствии с нормальным законом, т.е. дифференциальная функция распределения вероятности описывается выражением

тогда энтропия результата измерения с учетом погрешностей

Таким образом, интервал неопределенности будет равен Величина полученного с использованием информационных подходов интервала неопределенности соответствует интервалу, рассчитываемому с помощью неравенства Чебышева при вероятности примерно 0,95.

2. Анализ измерительных сигналов как случайных функций