4.2.3.Обработка результатов аппроксимации при использовании метода планирования экспериментов

Экспериментальные результаты и результаты расчетов при использовании метода планирования экспериментов вносят в таблицу (таблица 4), которая называется матрицей планирования. Часть таблицы, включающая только значения независимых переменных, является планом эксперимента. Графическая интерпретация результатов приведена на рис.29.

Анализ результатов при планировании эксперимента: заключается в оценке дисперсии результатов измерения, оценке адекватности и оценке значимости коэффициентов выбранной модели.

1. Проверка равноточности проведенных измерений может быть проведена с помощью критерия Кохрена (критерия равноточности) ,

где - дисперсия i-го эксперимента.

Полученное значение критерия при принятом уровне значимости сравнивают с табличным значением (Приложение 2). Если , результаты измерений считаются равноточными и их погрешность оценивается погрешностью определения среднего значения

.

Организационно-технические мероприятия

9Таблица 4

Форма матрицы планирования

Номер измерения в каждой серии	Номер серии измерений
	1	…	i	…	N
1		…		…
…
j		…		…
…
m		…		…
Среднее значение параметра в серии измерений		…		…

2. Адекватность выбранной модели проверяют с помощью критерия Фишера , где

- дисперсия адекватности; s – число параметров аппроксимирующей зависимости, определенных методом наименьших квадратов (число коэффициентов полинома).

Если , модель адекватна экспериментальным данным. Критерий применим только при . Если неравенство не выполняется – необходимо уточнить аппроксимирующую зависимость.

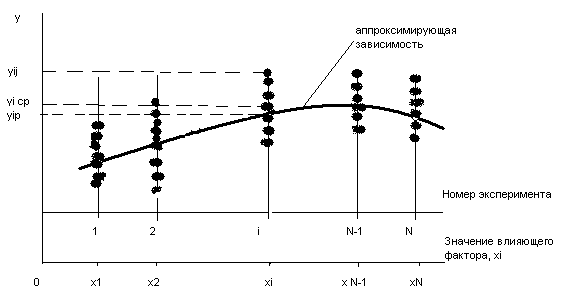
Рис.29. Графическое представление результатов измерения при использовании планирования эксперимента: – среднее значение в i-м эксперименте; y­_ip­ – значение, определенное с помощью аппроксимирующей зависимости

3.Оценка значимости коэффициентов аппроксимирующей зависимости

Коэффициенты полинома (аппрокс.завис.) в различной степени влияют на выходной параметр и на точность модели. Коэффициенты при линейных членах полинома при отсутствии других членов являются частными производными функции отклика по соответствующим переменным, т.е. значения коэффициентов являются количественной мерой, определяющей влияние каждого фактора. Знак коэффициента определяет характер зависимости функции отклика от соответствующего фактора. Коэффициенты при квадратичных членах характеризуют степень нелинейности функции отклика и т.п.

Оценку значимости коэффициентов с точки зрения отличия от нуля можно проводить с помощью критерия Стьюдента , где - дисперсия коэффициента ; .

При этом решают систему нормальных уравнений относительно коэффициентов , но правые части уравнений заменяют на , при этом ,получают зависимости

Подставляя =1 и принимая остальные , находят , т.е. и т.д. Таким образом, дисперсии коэффициентов будут равны

и т.д.

Значения сравнивают с табличными значениями (Приложение 3). При коэффициент считается незначимым и может быть исключен из модели.