4.2. Нахождение статистических зависимостей с использованием планирования экспериментов

Интерполяция экспериментальных данных и оценка погрешностей и неопределенностей результатов измерения позволяют выявлять закономерности между значениями выходных параметров и вариантами сочетаний влияющих факторов, т.е. решать типичную задачу построения многофакторной эмпирической модели по экспериментальным данным. Решение таких задач относится к математическому направлению, которое носит название планирования экспериментов. Это направление подразумевает использование таких математических методов, как метод минимальных квадратов, регрессионный анализ, многофакторный анализ и т.д., подчиняя эти методы одной цели – выбору математической модели, описывающей статистические данные.

В то же время методы, используемые в планировании экспериментов, дополняют друг друга, позволяют учитывать особенности полученных результатов измерения. Так метод минимальных квадратов, позволяющий определять параметры аппроксимирующей зависимости, становится регрессионным анализом, как только переходят к статистическим оценкам параметров этой зависимости.

4.2.1.Выбор входных и выходных переменных

Входные параметры, которые оказывают влияние на состояние объекта и могут быть измерены, называют факторами. Каждый фактор характеризуется областью определения, которая должна быть установлена до проведения измерений. Эта область может быть дискретной или непрерывной, причем, во втором случае проводят искусственную дискретизацию.

ГРАНИЦЫ области определения каждого отдельного фактора Обусловлены:

- его физической природой (значения яркости изображения при оценке качества изображения соответствуют зрительному восприятию),

- конкретными условиями, характерными для данного объекта исследования (временем действия, условиями в кинотеатре, стоимостью оборудования),

- возможностью совмещения факторов и т.д.

Каждую конкретную комбинацию факторов можно рассматривать как точку в многомерном факторном пространстве. Для того чтобы получить как можно больший объем статистических экспериментальных данных, на которых основывается формулируемая математическая модель, необходимо рассмотреть возможности моделирования значений влияющих факторов, т.е. их достаточную управляемость.

Область возможных комбинаций факторов называют областью возможных планов эксперимента или факторным пространством . Графическое изображение области возможных планов эксперимента при двухфакторном эксперименте приведено на рис.28.

Выходной параметр Y , определяющий состояние объекта, может быть принят за критерий оптимальности, целевую функцию. Графическое изображение этой функции называют поверхностью отклика. Ее значение зависит от значений входных параметров.

Выходными характеристиками могут быть

- экономические (стоимость, производительность),

- технологические (точность, качество),

= конструктивные,

- надежностные (вероятность безотказной работы) параметры.

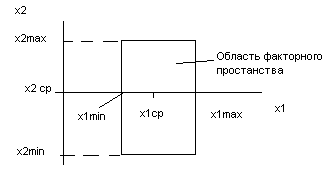
Рис.28. Графическое изображение области возможных планов двухфакторного эксперимента