2.6. Соотношение между погрешностями и результатами измерений

2.7.Виды моделей, которые могут быть использованы для описания измерительных систем

Для описания измерительных систем могут быть использованы концептуальные, факторные и математические модели.

Концептуальные модели целесообразно использовать для предварительного описания системы. Эта модель включает:

- границы анализируемой системы,

- цели существования системы,

- возможности перехода от качественного описания системы к количественному,

- прямые и обратные связи между элементами.

На рис. 20 приведена концептуальная модель отдельной метрологической процедуры, используемой в измерительной системе.

Рис. 20. Пример концептуальной модели

На основе концептуальной модели строится факторная модель, устанавливающая логические связи между параметрами (входными, выходными), факторами внешней среды и параметрами управления. Эта модель предусматривает анализ обратных связей. Пример факторной модели приведен на рис.21.

Подробная проработка двух приведенных выше моделей является основой формирования математических моделей, описывающих измерительную систему и ее отдельные элементы. Как правило, статические процессы описываются алгебраическими выражениями, динамические – дифференциальными уравнениями. Математическая модель называется статической, если входные величины реализуются в виде отдельных точек, тогда выходной параметр измерительной системы . Такие модели являются детерминированными.

При моделировании широко используются методы преобразования экспериментальных значений в аналитический вид

Переход от факторной модели к математической проводится с использованием методов интерполяции, аппроксимации, экстраполяции.

Интерполяция – приближенное или точное нахождение величины по известным отдельным значениям этой же величины или другой, с ней связанной (пусть имеется n точек, подбирают интерполирующую функцию, проходящую через эти точки). Аппроксимация – замена одних математических объектов другими, например, статистических аналитическими, в том или ином смысле, близкими к исходным. Экстраполяция – продолжение функции за пределы ее области определения.

2.8.Модели измерений

Как правило, измерение физической величины предполагает нахождение ее значения опытным путем, с помощью специальных технических средств.

Модели измерений могут быть: исходные, приведенные и, наконец, математические модели.

Исходная модель измерения по степени проработки является факторной моделью, представлена на рис. 22

Внутренние помехи в системе возникают по причине:

- нестабильности характеристик отдельных элементов средства измерения,

- износа, разрегулировок,

- нестабильности физико- механических свойств и т.п. Внешние помехи могут возникать:

- при изменении внешних условий: электромагнитных наводок, засветки измерительной шкалы, изменении температуры, относительной влажности, при возникновении шумов, вибраций.

Степень влияния того или иного фактора определяется, в первую очередь, принципом действия средства измерения.

Рис. 21. Факторная модель измерительной процедуры

Пользуясь обратной характеристикой средства измерения, по выходному сигналу определяют результат измерения y [38]. Если бы помехи отсутствовали, результат измерения точно определял измеряемую величину , но .

Погрешность измерения будет равна , т.е. разности между результатом измерения и измеряемой величиной. Результат измерения при этом . Данное выражение называется приведенной моделью измерения, поскольку y и z являются приведенными ко входу средства измерения сигналами и z­_1­',…,z­_n' . Графическое изображение данной модели дано на рис. 23.

Рис. 22. Исходная модель измерений: - полезный сигнал; φ – характеристика средства измерения; ; α – обратная характеристика средства измерения; z′ - дополнительный сигнал из-за помех

­_­

Рис.23. Приведенная модель измерений: си – средство измерения

Измеряемые величины в общем случае носят случайный характер и представляют собой либо случайные величины, либо случайные функции, характеризуемые законами распределения вероятности появления того или иного количественного значения. При каждом конкретном измерении имеют дело с определенным значением (реализацией) случайной величины.

Таким образом, под измерением понимают совокупность (ансамбль) отдельных метрологических процедур измерения случайных, всякий раз новых реализаций случайной величины. Модель измерений, учитывающая случайный характер измеряемых величин, должна включать измеряемые величины X, распределение вероятности которых описывается дифференциальной функцией распределения ; погрешности Z измерения случайной величины X данным средством измерения, вероятность которых распределена в соответствии с дифференциальной функцией распределения вероятности ; результаты измерения Y случайной величины X , распределение вероятности которых описывается дифференциальной функцией распределения вероятности . Случайные величины обозначены заглавным буквами, а их отдельные значения (реализации) – строчными.

В этом случае результат измерения является случайной величиной Y, представляющей ансамбль отдельных значений результатов измерений при измерениях отдельных, каждый раз новых значений x. Погрешность измерения – случайная величина Z, представляющая собой ансамбль отдельных значений погрешностей, с которыми проводятся эти измерения. Из математической модели измерения случайной величины следует, что результат измерения связан вероятностной зависимостью с измеряемой величиной, а погрешности и измеряемые величины также могут быть зависимыми величинами.

Математическая модель измерения случайной величины - математическое описание связей и отношений между реальными элементами анализируемой системы. Поскольку в этой модели используются случайные величины, такая модель также называется вероятностной или стохастической.

Погрешность Z характеризуется условной плотностью распределения вероятности случайной величины z при данном значении x, т.е. . Поскольку в общем случае Z зависит от X, т.е. распределение погрешности средства измерения при разных значениях x различно, эту погрешность средства измерения определяют в результате многократных измерений одной и той же известной величины x.

По полученным результатам находят условную плотность распределения вероятности результата измерения Y при данном значении x, т.е. . Этой плотности соответствует - математическое ожидание Y при данном x и (среднеквадратическом отклонении Y при данном x) (рис.24). Так как , перенеся начало координат функции в точку x, можно перейти к функции . Функция не зависит от плотности распределения случайной величины x, поэтому является объективной характеристикой метрологических параметров средства измерения и методики выполнения измерения.

Если погрешность характеризуется условной плотность распределения вероятности, то статистические характеристики этой погрешности являются условными характеристиками

;

;

.

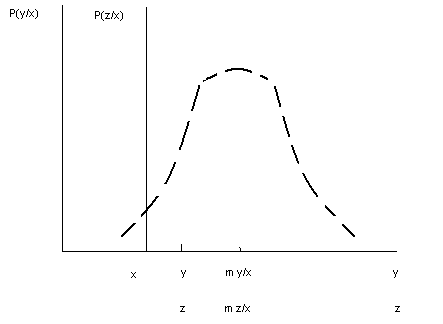
Рис.24. Условная плотность распределения вероятности случайной величины.