1.1. Формально- логические принципы измерений

Смысл измерений в различных науках интерпретируется по-разному. В широком смысле измерение рассматривается как инструмент процесса познания. Существуют две формы познания: чувственное познание, при котором человек получает чувственные впечатления, они могут быть выражены в форме определенных суждений; логическое познание, включающее анализ, синтез, истолкование, умозаключение, т.е. процессы, происходящие на абстрактном уровне. Только на логическом уровне формулируются вопросы, гипотезы, обнаруживаются отношения, взаимосвязи между объектами и характеристиками.

В соответствии с формами познания, измерения также могут быть физическими, психофическими (сенсорными), в основе которых лежат ощущения, возникающие в различных анализаторах человека, и интеллектуальными (логическими,), основанными на предшествующем опыте, мнениях, суждениях человека, проводящего оценку или измерение. Основа чувственного и логического измерения – наблюдения и эксперименты, причем, результат измерения должен удовлетворять требованиям объективной истины. Примером психофизических измерений в кинематографии являются субъективная оценка качества изображения и звука. Пример интеллектуальных (логических) измерений – оценка качества определенных изделий киновидеотехники по дифференциальным характеристикам, интегральная оценка изделий, интегральная оценка услуг по киновидеообслуживанию зрителей, являющаяся основой их сертификации, и т.д.

Объектом измерения является какая- либо характеристика определенного объекта или явления, эта характеристика может находиться в различных состояниях.

Количество сост.хар-ки влияет на выбор метода и средства изм.

4.1.1.Количество заметных градаций яркости

1) Количество заметных градаций яркости зрительного анализатора реагирует не на абсолютное изменение яркости, а на её относительное значение. Минимальное относительное изменение яркости ∆L / L — разностный порог различения. В определённых случаях, он постоянен. Минимальное заметное приращение ощущения

∆ε = k · ∆L / L;

k — коэффициент пропорциональности для абсолютно мелких приращений

dε = k · dL / L.

Интегрируя, получаем:

ε = k · lnL + D.**

При ε = 0 D = -k · lnL_{n !!!!!}

- пороговое. Тогда **

ε = k · ln(L / Ln)

Ощущение, приведённое к пороговому значению яркости. Закон Вебера-Фехнера справедлив в области яркостей 0,1 < L < 1000.кд/м кв

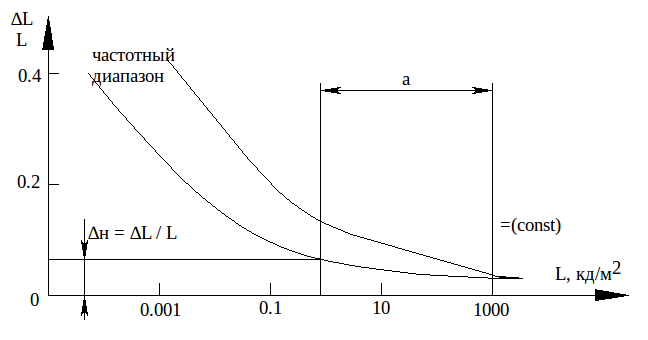
А разностный порог различия зависит от уровня яркости.

2) Определим число различимых градаций яркости для области а на примере ступенчатого клина яркостей с пороговым значением различения по яркости на каждой ступени. Первая ступень различима, если:

L₁ = L_ф + L_ф ∆_н = L_ф (1+ ∆_н);

L₂ = L₁ + L₁ ∆_н = L₁ (1+ ∆_н) = L_ф (1+ ∆_н)²;

L₃ = L_ф (1 + ∆_н)³;

…

L_n = L_ф (1 + ∆_н)^N;

Если известен относительный разностный порог, то

ln (L_N / L_ф) = N ln (1+ ∆_н);

∆_н = ∆L / L;

L_N / L_ф = k — контраст изображения ступенчатого клина

N = ln k / ln (1 + ∆n)

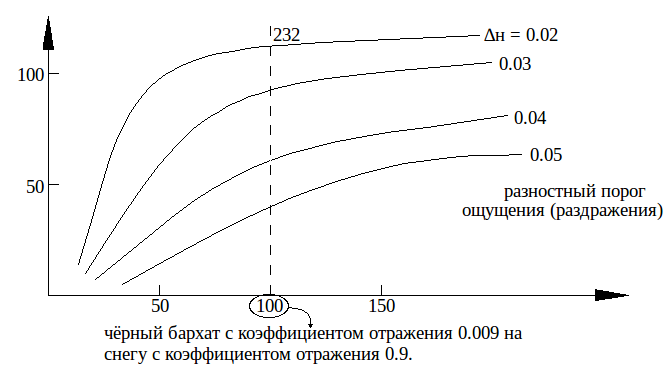
к > 100 — это контраст ч/б изображения на экране ТК в затемнённом помещении.

Разрешающая способность ЗА

О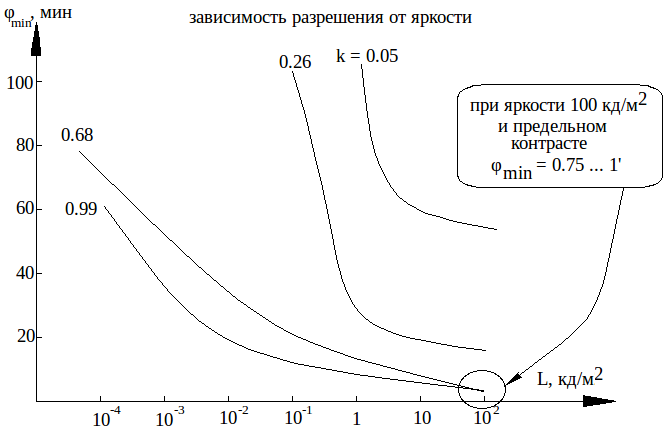 пределяется минимальным углом разрешения (т. е. влиянием хроматической аберрации в хрусталике, также как в оптических приборах).

Какова необходимая степень дискретизации изображения? (число элементов в поле изображения) — определяют пороговые характеристики зрения.

Как ЗА реагирует на снижение чёткости по сравнению с предельной? (Рыфтин, 1933)

Экспертам предлагалось выбрать отличное по восприятию качества изображение из серии изображений, полученных с различной степенью дискретизации. Приращение чёткости ∆G = ρ ∆_n / n, где ρ — коэффициент пропорциональности, а ∆_n / n — относительное приращение числа элементов.

dG = ρ d_n / n, интегрируя получим:

G = ρ ∫ d_n / n = ρ ln(n) + С.

При G = ln(n) и ρ = 1 → С = 0.

При G = 1 / ln(n) и n = n_max, ρ = ln(n_max). Тогда

G = ln n / ln (nmax)

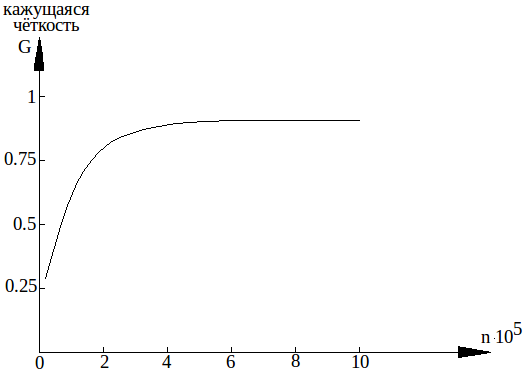
n_max = 8·10⁵ (при числе строк 800 и формате кадра 4/3).

Уменьшение числа элементов в два раза приводит к снижению G до ≈0.95 (на 5%). При малом числеэлементов — к существенному изменению кажущейся чёткости.

Число состояний характеристики, т.е. заметных градаций ее измерения, определяется физической природой характеристики, диапазоном ее изменения; множеством объектов, имеющих эту характеристику; возможностями субъекта измерения (в первую очередь, его дифференциальной чувствительностью).

Отображение характеристик объекта в область символов, выражающих значения состояний характеристик – это переход из реальной области в область абстракции (рис17,18).

Образом действительности является отображение

f – функция преобразования.

Для всех элементов множества {a} существует обратное отображение (при этом a ). Символ означает отображение, обратное по отношению к f. Множества и могут иметь разную мощность – могут существовать элементы множества , которые не отображаются ни в один из элементов множества .В свою очередь, отображение f­_Q­­ называется шкалой величины Q.