3.3. Дискретизация измерительных сигналов

Дискретизация измерительных сигналов по уровню (квантование) выполняется автоматически в цифровых измерительных приборах и аналого- цифровых преобразователях; при численной регистрации результатов, считываемых со шкалы аналогового прибора; при отнесении значения непрерывной величины к разрешенному значению шкалы, при округлении результата измерения.

Аналого- цифровые преобразователи выдают значения в соответствии со значениями измеряемой величины, а цифровые отсчетные устройства воспроизводят значения измеряемых величин в цифровой форме. Аналого- цифровые преобразователи не только являются составной частью цифровых измерительных приборов (в которые также входят цифро- аналоговые преобразователи), информационно- измерительных систем, но выпускаются и автономном виде (в виде интегральных микросхем).

Автономные аналого- цифровые преобразователи не имеют десятичного отсчетного устройства, дают на выходе только закодированные значения, являются более быстродействующими, но менее точными. Результатом комплексного подхода к данной проблеме являются аналого- дискретные измерительные приборы, их отсчетные устройства являются квазианалоговыми, в них роль указателя выполняет, например, светящаяся полоса или точка, дискретно меняющие свою длину или положение, причем, значения последних параметров управляются кодом. Как цифровые измерительные приборы, так и аналого- дискретные измерительные приборы, по сути, являются цифровыми измерительными устройствами, в которых непрерывная измеряемая величина дискретизируется во времени и квантуется по уровню (рис.12).

Примером аналого- цифрового преобразования сигнала является запись сигнала на компакт- диск. При этом записываемый сигнал под воздействием лазерного луча записывается в виде цифрового сигнала, в котором наличие или отсутствие углубления (пита) на диске определяет цифру. При воспроизведении сигнал опять преобразовывают в аналоговый, т.е. происходит цифро- аналоговое преобразование. Таким образом, дискретизацией измерительных сигналов по уровню, или квантованием называется дискретизация множества значений непрерывного сигнала [44,45]. При этом необходимо различать уровень квантования, x­_кв­, т.е. одно из значений непрерывного сигнала, полученное в результате его квантования, и шаг квантования, , т.е. разность между соседними уровнями квантования.

Дискретизация по уровню приводит к появлению методической погрешности (шума квантования). Эта погрешность является неслучайной функцией случайного значения измеряемой величины.

В практике использования информационно- измерительных систем наибольшее распространение получило равномерное квантование, при котором весь диапазон значений измеряемой величины разбивается на одинаковые интервалы, длина каждого интервала – шаг

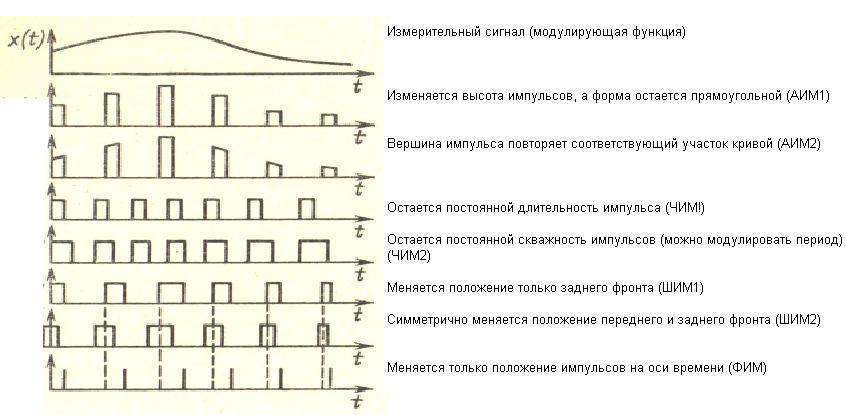
Рис.11. Виды импульсной модуляции измерительных сигналов

Рис.12. Дискретизация непрерывной измеряемой величины во времени и по уровню в цифровом измерительном устройстве

квантования (рис.13). Если , то закон распределения погрешности квантования равномерен (не зависит от закона распределения вероятности измеряемой величины), если нет, погрешность квантования распределена по такому же закону, как и изменяемая величина.

Погрешность квантования в том случае, когда за уровень квантования принимается нижняя или верхняя граница интервала квантования, равна шагу квантования . Если за уровень квантования принимается середина интервала, погрешность квантования равна половине шага квантования, т.е. = , а математическое ожидание погрешности . Дисперсия погрешности для всех трех случаев .

При этом среднеквадратическое значение равно .

Неравномерное квантование целесообразно использовать, когда закон распределения вероятностей значений измеряемой величины отличается от равномерного, а число уровней квантования мало ( ). При этом в области больших значений плотности вероятности шаг квантования делается меньше.

Под дискретизацией измерительных сигналов по времени , понимают дискретное представление непрерывного сигнала X(t) в функцию ,по которой может быть получено исходное значение сигнала. Дискретизация по времени может быть осуществлена такими способами, как представление функции мгновенными дискретными значениями или замена непрерывной функции рядом коэффициентов разложении по выбранной системе базисных функций (при этом по каналу связи передаются только коэффициенты разложения). Первый способ используется чаще.

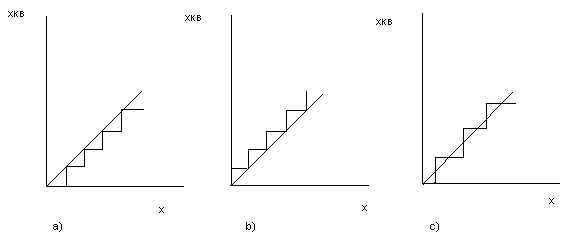
Рис.13. Разновидности равномерного квантования измерительных сигналов: а – за уровень квантования принимается нижняя граница интервала квантования; b – за уровень квантования принимается верхняя граница интервала квантования; с- за уровень квантования принимается середина интервала квантования

Основной теоретической проблемой дискретизации измерительных сигналов по времени является выбор шага дискретизации, эта проблема решается в рамках теоремы Котельникова В.А. (1933 г.) [45]. В соответствии с этой теоремой, если функция, описывающая измерительный сигнал, удовлетворяет условиям Дирихле (ограничена, кусочно- непрерывна, имеет конечное число экстремумов), ее спектр ограничен некоторой частотой , то существует такой максимальный интервал между отсчетами, при котором имеется возможность безошибочного восстановления дискретизируемой функции по дискретным отсчетам, этот интервал , где носит название частоты Найквиста.