Билет № 9

Системы счисления. Позиционные и непозиционные. Представление чисел в системе счисления с основанием q. Десятичная, двоичная, восьмеричная, шестнадцатеричная системы счисления.

Совокупность правил записи и именования чисел называют системой счисления. Числа записываются с помощью символов, по кол-ву которых определяют системы счисления на позиционные и непозиционные. Если для записи чисел используется условно бесконечное число символов, то система счисления – непозиционная.(римская система счисления). Бесконечный ряд чисел в такой системе счисления требует бесконечного кол-ва символов для записи чисел.

В противовес непозиционной системе счисления, позиционные используют ограниченный набор символов для записи чисел, причем эти символы называют цифрами. Величина числа зависит не только от использованных цифр, но и от места их записи в числе(Например: 215, 521, 251). Кол-во цифр, используемых для записи числа называют основанием системы счисления. В повседневной жизни мы используем позиционную десятичную систему счисления с основанием 10. Правила записи чисел в десятичной СС:

1. Числа от 0 до 9 записываются соответствующими цифрами.

2. Поскольку для записи следующего числа цифры не существует, вместо 9 начинают писать 0, но добавляют слева еще один разряд, который называется старшим, где записывается единица, тем самым получаем число 10, далее идут числа 11, 12 и т.д.(до 19), а для записи следующего числа “*9” снова обращается в 0, но левый старший разряд увеличивается на 1, получаем 20 и т.д.

3. Теперь заполненными являются 2 разряда полностью, оба разряда заменяются на 0, а слева добавляется третий разряд еще более старший со значением 1 и т.д.

4. Таким образом используя конечное число цифр можно записать любое сколь угодно большое число

Важным преимуществом позиционной СС. над непозиционной является простота выполнения операций над такими числами. Любое число позиционной системы счисления с основанием q может быть представлена в виде формулы

1011002 = 1 · 2⁵ + 0 · 2⁴ + 1 · 2³ + 1 · 2² + 0 · 2¹ + 0 · 20 = 1 · 32 + 0 · 16 + 1 · 8 + 1 · 4 + 0 · 2 + 0 · 1 = 32 + 8 + 4 + 0 = 4410

Вследствие применения ЭВМ, в информатике большое значение имеют СС. с основанием q = 2. Тем не менее недостатком двоичной СС. является излишне громоздкая запись чисел. По сравнению с 10-чной записью числа, 2-чная длиннее в 3.3 раза, что очень неудобно для восприятия т.к. обычно человек способен воспринимать 5-7 цифр одновременно. Т.о. удобнее пользоваться числами, длина которых составляет до 4 знаков или цифр, максимум до 5–7. При этом желательно существование достаточно простых методов преобразования таких записей чисел в двоичную с.с. и обратно. Исторически в качестве таких альтернатив двоичной системе счисления были выбраны восьмеричная и шестнадцатеричная с.с. Процессы преобразования данных систем друг в друга в значительной степени проще взаимного преобразования. При этом запись чисел в восьмеричной с.с. в 3 раза короче, а в 16-ричной в 4 раза короче двоичной с.с.

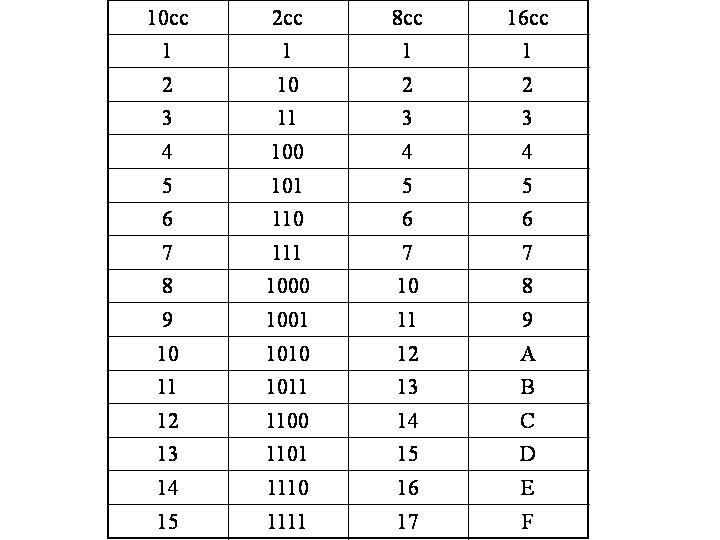
Восьмеричная с.с. оперирует набором из 8 чисел.

Шестнадцатеричная оперирует шестнадцатью знаками, причем первые 10 совпадают с цифрами десятичной с.с. а начиная с 10 латинские буквы.

В некоторых ситуациях может быть неясен контекст представления чисел, поскольку в 10-чной, 8-чной и 16-чной системы могут существовать числа разной велечины.

Для преодоления такой ситуации к числу добавляют основание с.с.(23110 = 111001112 = 3478 = Е716)