Билет № 21 Табличное и алгебраическое задание булевских функций. Коституента единицы и коституента нуля.

Если задана булева функция в виде формулы, то можно построить таблицу истинности, вычисляя ее значения на каждом из наборов.

Пример 4.

Дана булева функция

Необходимо построить ее таблицу истинности.

Решение.

Функция трех переменных имеет всего восемь значений. Каждое получается на соответствующем наборе, начиная с набора

0,0,0 (x₁ = 0, x₂ = 0, x₃ = 0),

кончая набором

1,1,1 (x₁ = 1, x₂ = 1, x₃ = 1).

При вычислении пользуемся соотношениями:

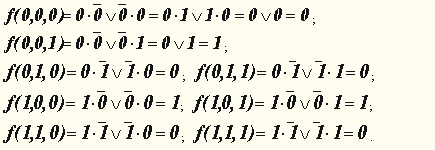
Результаты сведем в таблицу:

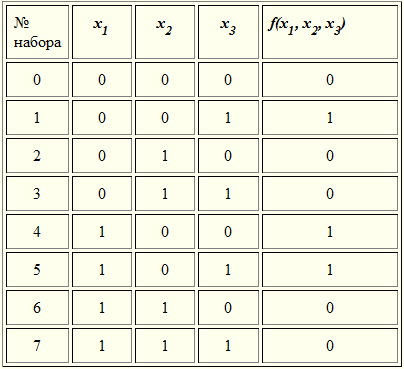
Аналитическое представление булевых функций

Конституенты единицы . Булеву функцию, равную 1 только на одном наборе аргументов, называют конституентой единицы . Будем обозначать конституенту единицы, зависящую от n аргументов, символом : , где N - номер конституенты, равный номеру набора, на котором она равна 1.

записывают в виде конъюнкции всех аргументов, взятых с отрицаниями или без них, по правилу: отрицания ставятся над аргументами, которые на наборе с номером N равны 0.

Перечислить конституенты 1 функции, представленной таблицей истинности примера 4.

Решение.

Конституенты нуля . Булеву функцию, равную 0 только на одном наборе аргументов, называют конституентой нуля. Будем обозначать конституенту нуля, зависящую от n аргументов, символом , где N - номер конституенты, равный номеру набора, на котором она равна 0.

записывают в виде дизъюнкции всех аргументов, взятых с отрицаниями или без них по правилу: отрицания ставятся над аргументами, которые на наборе с номером N равны 1.

Пример 6.

Перечислить конституенты 0 логической функции, заданной в примере 4.

Решение.

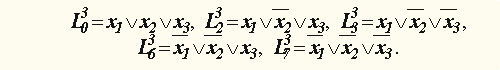
Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы булевой функции .

Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы (СДНФ и СКНФ) относятся к числу канонических форм представления функций. Любая булева функция представима в СДНФ (кроме константы 0) и СКНФ (кроме константы 1). Запись произвольной булевой функции в этих формах проста и удобна для последующих преобразований. СДНФ и СКНФ у каждой функции единственны.

СДНФ функции есть дизъюнкция всех ее конституент единицы.

Записать в СДНФ булеву функцию, заданную таблицей примера 4. Решение.

Конституенты 1 этой функции представлены в примере 5. Объединим их знаком дизъюнкции:

СКНФ функции есть конъюнкция всех ее конституент нуля.

Записать в СКНФ булеву функцию из примера 4.

Решение.

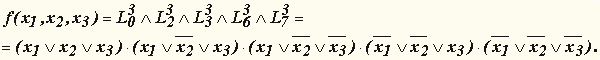
Билет № 22

Базовая система элементов компьютерных систем. Элемент «Логическое ИЛИ». Элемент «Логическое И». Элемент «Логическое НЕ». Обозначения. Сигналы, эквивалентные электрические схемы.

Базовая система элементов компьютерных систем

Для построения цифровых устройств была выбрана двоичная система счисления. Для проектирования устройств можно было использовать мощный аппарат алгебры логики – булевых функций. При построении функциональных узлов КС используются элементы, которые реализуют базовую систему логических функций. Одним из таких базовых наборов является набор из трёх функций: дизъюнкции (логическое ИЛИ), конъюнкции (логическое И) и отрицание (логическое НЕ). показаны условные обозначения и значения выходного сигнала в зависимости от входных сигналов. Ноль изо бражается на диаграммах низким значением сигнала, а единица – высоким. 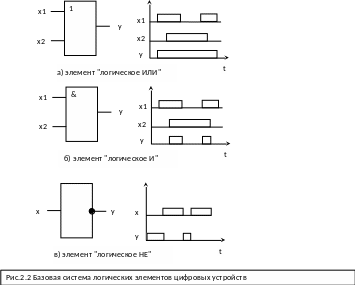Используя эти базовые э лементы, строятся все функциональные узлы ЦВМ.