Билет № 19 Основные понятия алгебры Буля. Логические операции: отрицание конъюнкция, дизъюнкция, импликация и эквиваленция. Порядок логических операций.

Алгебра логики - часть математической логики, которая занимается исчислением высказываний.

Высказывание - утверждение, которое может быть истинным («да») или ложным («нет»). Одно и то же высказывание не может быть одновременно истинным и ложным. Поэтому в алгебре логики рассматриваются только два значения высказываний:

1) истинное (ему присваивается значение 1)

2) ложное (ему присваивается значение 0)

В логических задачах исходными данными являются не только числа, но и сложные и весьма запутанные высказывания. Простые высказывания являются простейшим объектом логики высказываний.

Базовыми элементами, которыми оперирует алгебра логики, являются высказывания. Высказывания строятся над множеством, над элементами которого определены три операции:

• Отрицание— логическая операция над суждениями, результатом которой является суждение (в известном смысле) «противоположное» исходному. Обозначается знаком ¬ перед или чертой над суждением. Синоним: логическое "НЕ".

• Конъюнкция (от лат. conjunctio союз, связь) — логическая операция, по своему применению максимально приближённая к союзу "и". Синонимы: логическое "И", логическое умножение, иногда просто "И". Конъюнкция может быть бинарной операцией, то есть, иметь два операнда, тернарной операцией, т.е. иметь три операнда или n-арной операцией, т.е. иметь n операндов.

• Дизъюнкция (лат. disjunctio — разобщение), логическое сложение, логическое ИЛИ, включающее ИЛИ; иногда просто ИЛИ — логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу». Дизъюнкция может быть бинарной операцией (иметь два операнда), тернарной операцией (иметь три операнда) или n-арной операцией (иметь n операндов).

• Импликация (лат. implicatio — связь) — бинарная логическая связка, по своему применению приближенная к союзам «если… то…». Импликация записывается как посылка → следствие; применяются также стрелки другой формы и направленные в другую сторону (остриё всегда указывает на следствие). Результатом ИМПЛИКАЦИИ является ЛОЖЬ только тогда, когда условие А истинно, а следствие В ложно.

• Эквивале́нция (или эквивале́нтность) — двуместная логическая операция. Обычно обозначается символом ≡ или ↔. ЭКВИВАЛЕНТНОСТЬ - определяет результат сравнения двух простых логических выражений А и В. Результатом ЭКВИВАЛЕНТНОСТИ является новое логическое выражение, которое будет истинным тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны. Обозначается символом "эквивалентности"

Порядок выполнения логических операций в сложном логическом выражении:

1. инверсия

2. Конъюнкция

3. дизъюнкция

4. Импликация

5. Эквивалентность

Билет № 20 Зависимости между логическими операциями. Дизъюнктивная и конъюнктивная нормальные формы представления логических выражений.

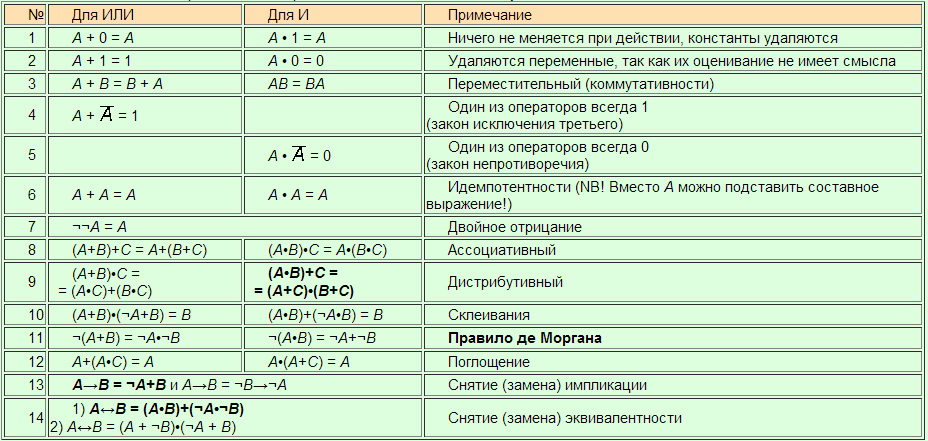
Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ. Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем.

Алгоритм построения ДНФ

1. Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:

2. Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:

3. Избавиться от знаков двойного отрицания.

4. Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.

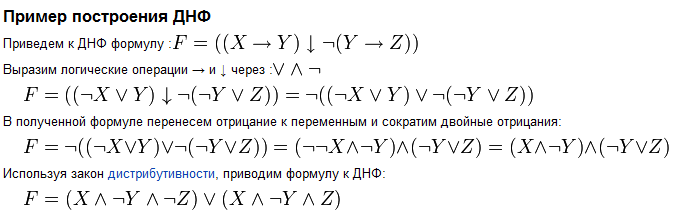
Конъюнкти́вная норма́льная фо́рма (КНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид конъюнкции дизъюнкций литералов. Конъюнктивная нормальная форма удобна для автоматического доказательства теорем. Любая булева формула может быть приведена к КНФ. Для этого можно использовать: Закон двойного отрицания, Закон де Моргана, Дистрибутивность.

Алгоритм построения КНФ

1. Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:

2. Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:

3. Избавиться от знаков двойного отрицания.

4. Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.