Билет № 16 Понятие о сжатии информации.
Сжатие данных (англ. data compression) — алгоритмическое преобразование данных, производимое с целью уменьшения их объёма. Применяется для более рационального использования устройств хранения и передачи данных. Синонимы — упаковка данных, компрессия, сжимающее кодирование, кодирование источника. Обратная процедура называется восстановлением данных (распаковкой, декомпрессией).
Сжатие основано на устранении избыточности, содержащейся в исходных данных. Простейшим примером избыточности является повторение в тексте фрагментов (например, слов естественного или машинного языка). Подобная избыточность обычно устраняется заменой повторяющейся последовательности ссылкой на уже закодированный фрагмент с указанием его длины. Другой вид избыточности связан с тем, что некоторые значения в сжимаемых данных встречаются чаще других. Сокращение объёма данных достигается за счёт замены часто встречающихся данных короткими кодовыми словами, а редких — длинными (энтропийное кодирование). Сжатие данных, не обладающих свойством избыточности (например, случайный сигнал или белый шум, зашифрованные сообщения), принципиально невозможно без потерь.
В основе любого способа сжатия лежит модель источника данных, или, точнее, модель избыточности. Иными словами, для сжатия данных используются некоторые априорные сведения о том, какого рода данные сжимаются. Не обладая такими сведениями об источнике, невозможно сделать никаких предположений о преобразовании, которое позволило бы уменьшить объём сообщения. Модель избыточности может быть статической, неизменной для всего сжимаемого сообщения, либо строиться или параметризоваться на этапе сжатия (и восстановления). Методы, позволяющие на основе входных данных изменять модель избыточности информации, называются адаптивными. Неадаптивными являются обычно узкоспециализированные алгоритмы, применяемые для работы с данными, обладающими хорошо определёнными и неизменными характеристиками. Подавляющая часть достаточно универсальных алгоритмов являются в той или иной мере адаптивными.
Все методы сжатия данных делятся на два основных класса:
Сжатие без потерь
Сжатие с потерями
При использовании сжатия без потерь возможно полное восстановление исходных данных, сжатие с потерями позволяет восстановить данные с искажениями, обычно несущественными с точки зрения дальнейшего использования восстановленных данных. Сжатие без потерь обычно используется для передачи и хранения текстовых данных, компьютерных программ, реже — для сокращения объёма аудио- и видеоданных, цифровых фотографий и т. п., в случаях, когда искажения недопустимы или нежелательны.
Сжатие с потерями, обладающее значительно большей, чем сжатие без потерь, эффективностью, обычно применяется для сокращения объёма аудио- и видеоданных и цифровых фотографий в тех случаях, когда такое сокращение является приоритетным, а полное соответствие исходных и восстановленных данных не требуется.
Билет № 17 Структуры данных. Линейная. Табличная. Иерархическая.
Работа с большими наборами данных автоматизируется проще, когда данные упорядочены, то есть образуют заданную структуру. Существует три основных типа структур данных:
• линейная,
• иерархическая,
• табличная.
Линейные структуры — это хорошо знакомые нам списки. Список — это простейшая структура данных, отличающаяся тем, что каждый элемент данных однозначно определяется своим номером в массиве. Проставляя номера на отдельных страницах рассыпанной книги, мы создаем структуру списка. Обычный журнал посещаемости занятий, например, имеет структуру списка, поскольку все студенты группы зарегистрированы в нем под своими уникальными номерами. Мы называем номера уникальными потому, что в одной группе не могут быть зарегистрированы два студента с одним и тем же номером.
При создании любой структуры данных надо решить два вопроса: как разделять элементы данных между собой и как разыскивать нужные элементы. В журнале посещаемости, например, это решается так: каждый новый элемент списка заносится с новой строки, то есть разделителем является конец строки. Тогда нужный элемент можно разыскать по номеру строки.
N п/п Фамилия, Имя, Отчество
1 Аистов Александр Алексеевич
2 Бобров Борис Борисович
Разделителем может быть и какой-нибудь специальный символ. Нам хорошо известны разделители между словами — это пробелы. В русском и во многих европейских языках общепринятым разделителем предложений является точка. В рассмотренном нами классном журнале в качестве разделителя можно использовать любой символ, который не встречается в самих данных, например символ «*». Тогда наш список выглядел бы так:
Аистов Александр Алексеевич * Бобров Борис Борисович * Воробьева Валентина
Владиславовна *... * Сорокин Сергей Семенович
В этом случае для розыска элемента с номером я надо просмотреть список начиная с самого начала и пересчитать встретившиеся разделители. Когда будет отсчитано n- 1разделителей, начнется нужный элемент. Он закончится, когда будет встречен следующий разделитель.
Еще проще можно действовать, если все элементы списка имеют равную длину. В этом случае разделители в списке вообще не нужны. Для розыска элемента с номером и надо просмотреть список с самого начала и отсчитать а( n -1) символ, где а - длина элемента. Со следующего символа начнется нужный элемент. Его длина тоже равна а, поэтому его конец определить нетрудно. Такие упрощенные списки, состоящие из элементов равной длины, называют векторами данных. Работать с ними особенно удобно.
Таким образом, линейные структуры данных (списки) — это упорядоченные структуры, в которых адрес элемента однозначно определяется его номером.
При хранении табличных данных количество разделителей должно быть больше, чем для данных, имеющих структуру списка. Например, когда таблицы печатают в книгах, строки и столбцы разделяют графическими элементами — линиями вертикальной и горизонтальной разметки.
Если нужно сохранить таблицу в виде длинной символьной строки, используют один символ-разделитель между элементами, принадлежащими одной строке, и другой разделитель для отделения строк, например так:
Меркурий*0,39*0,056*0#Венера*0,67*0,88*0#Земля*1,0*1,0*1#Марс*1,51*0,1*2*...
Для розыска элемента, имеющего адрес ячейки ( m , n ), надо просмотреть набор данных с самого начала и пересчитать внешние разделители. Когда будет отсчитан m — 1 разделитель, надо пересчитывать внутренние разделители. После того как будет найден n — 1 разделитель, начнется нужный элемент. Он закончится, когда будет встречен любой очередной разделитель.
Еще проще можно действовать, если все элементы таблицы имеют равную длину. Такие таблицы называют матрицами . В данном случае разделители не нужны, поскольку все элементы имеют равную длину и количество их известно. Для розыска элемента с адресом ( m , n ) в матрице, имеющей М строк и N столбцов, надо просмотреть ее с самого начала и отсчитать a[N(m — 1) + ( n — 1)] символ, где а — длина одного элемента. Со следующего символа начнется нужный элемент. Его длина тоже равна а, поэтому его конец определить нетрудно.
Таким образом, табличные структуры данных (матрицы) — это упорядоченные структуры, в которых адрес элемента определяется номером строки и номером столбца, на пересечении которых находится ячейка, содержащая искомый элемент.
Многомерные таблицы . Выше мы рассмотрели пример таблицы, имеющей два измерения (строка и столбец), но в жизни нередко приходится иметь дело с таблицами, у которых количество измерений больше. Вот пример таблицы, с помощью которой может быть организован учет учащихся.
Размерность такой таблицы равна пяти, и для однозначного отыскания данных об учащемся в подобной структуре надо знать все пять параметров (координат).
Иерархические структуры данных
Нерегулярные данные, которые трудно представить в виде списка или таблицы, часто представляют в виде иерархических структур. С подобными структурами мы очень хорошо знакомы по обыденной жизни. Иерархическую структуру имеет система почтовых адресов. Подобные структуры также широко применяют в научных систематизациях и всевозможных классификациях. Смотрите рисунок ниже.
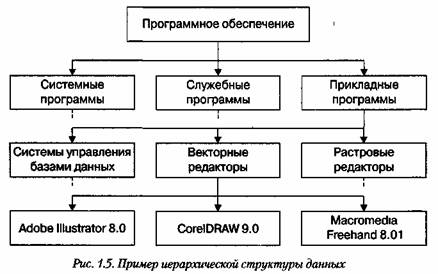
В иерархической структуре адрес каждого элемента определяется путем доступа (маршрутом), ведущим от вершины структуры к данному элементу. Вот, например, как выглядит путь доступа к команде, запускающей программу Калькулятор (стандартная программа компьютеров, работающих в операционной системе Windows):
Пуск > Программы > Стандартные > Калькулятор.
Дихотомия данных. Основным недостатком иерархических структур данных является увеличенный размер пути доступа. Очень часто бывает так, что длина маршрута оказывается больше, чем длина самих данных, к которым он ведет. Поэтому в информатике применяют методы для регуляризации иерархических структур с тем, чтобы сделать путь доступа компактным. Один из методов получил название дихотомии. Его суть понятна из примера, представленного на рисунке ниже.
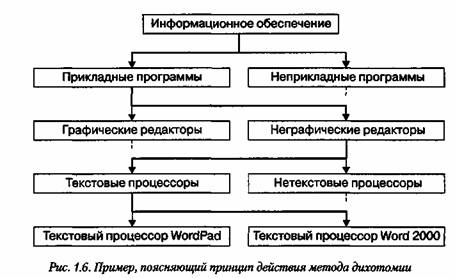
В иерархической структуре, построенной методом дихотомии, путь доступа к любому элементу можно представить как путь через рациональный лабиринт с поворотами налево (0) или направо (1) и, таким образом, выразить путь доступа в виде компактной двоичной записи. В нашем примере путь доступа к текстовому процессору Word 2000 выразится следующим двоичным числом: 1010.