10. Нагрев тонких тел при постоянной температуре печи. Температурно-тепловая диаграмма. Конвективный теплообмен

В этом случае тепловой поток определяется по формуле:

Диф. уравнение с учётом принимает вид:

Продолжительность нагрева:

Температура тела:

Лучистый теплообмен

При теплообмене излучением тепловой поток поверхности металла определяется по формуле:

- видимый коэфф. Излучения

11. Теория нагрева массивных тел. Уравнения теплопроводности для массивных тел. Принцип использования диаграммы будрина.

При решении задач теплопроводности для массивных тел используется диф. уравнение теплопроводности с соответствующими граничными и начальными условиями.

Призма (длинна соизмерима с шириной и толщиной) , – теплопроводность

Призма неограниченной длины (длина в 10 и более раз превышает ширину и толщину)

Пластина (длина и ширина в 10 и более раз превышает толщину)

Цилиндр ограниченной длины

Цилиндр неограниченной длины (длина в 10 и более раз превышает диаметр)

Шар (сфера)

Методы решения нагрева термически массивных тел

Решение диф. уравнения теплопроводности с соответствующими граничными и начальными условиями позволяет найти температурное поле для тел простейшей формы как функцию следующих переменных

1. 

t – текущая температура

x – расстояние от середины тела до рассматриваемой точки

– коэф. температуропроводности

– коэф. внешнего теплообмена

– безразмерные координаты

– критерий Фурье, безразмерное время

– критерий массивности тела

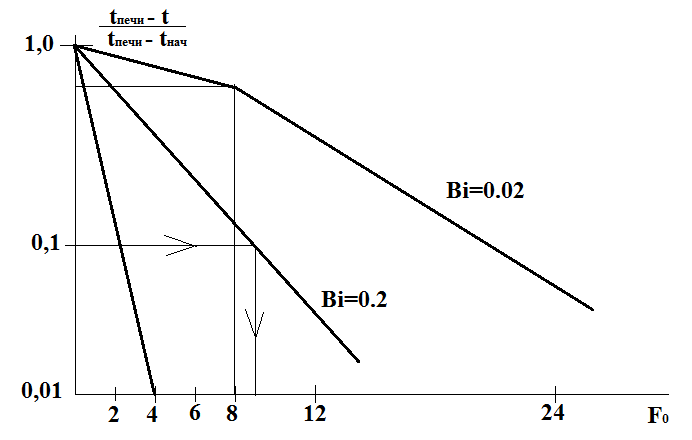
С использованием выражения (1) построены диаграммы Будрина, с помощью которых можно определить температуру в любой точке сечения тела при заданной t-ре печи и заданном времени нагрева. Или при заданной t-ре тела возможно определить необходимое время нагрева. Т.о. решение уравнения теплопроводности представляется в графическом виде.

Диаграммы составлены для пластины и цилиндра отдельно для центра ( ) и отдельно для поверхности ( )

по оси Х отложено безразмерное время, т.е. критерий Фурье.

По У – безразмерная температура

12. Использование численных методов решения задач нагрева.

Самым распространённым является метод конечных разностей. Суть: при этом диф. Уравнение записывается в форме конечных разностей. Отправной точкой метода является замена области решения разностной сеткой.

Для инженерных расчётов среди приближённых методов часто исп-ся методы термического слоя. В основу метода термического слоя положен принцип разбиения процесса нагрева на 2 этапа: инерционный(тепловой поток, падающий на пов-ть достигает центра тяжести) и регулярный

(происходит нагрев тела уже по всему сечению).