
- •Температурное поле. Температурный градиент.
- •Основные виды теплообмена. Теплопередача и теплоотдача.
- •Теплообмен:
- •Теплопроводность, закон фурье.
- •Стационарная теплопроводность однослойной и многослойной плоской стенки.
- •Граничные условия 1ого рода
- •Граничные условия 2ого рода
- •Граничные условия 3ого рода
- •Граничные условия 1ого рода
- •Стационарная теплопроводность однослойной цилиндрической стеши.
- •С тационарная теплопроводность многослойной цилиндрической стенки.
- •Граничные условия 3ого рода
- •Теплопроводность через стенки сложной конфигурации. Ребристые поверхности.
- •Нестационарная теплопроводность. Критерии био и старка. Термически тонкие и термически массивные тела.
- •Нагрев тонких тел при постоянной температуре печи. Температурно-тепловая диаграмма. Конвективный теплообмен
- •Лучистый теплообмен
- •Теория нагрева массивных тел. Уравнения теплопроводности для массивных тел. Принцип использования диаграммы будрина.
- •Методы решения нагрева термически массивных тел
- •Использование численных методов решения задач нагрева.
- •Конвективный теплообмен. Основные уравнения конвективного теплообмена.
- •Критерия подобия конвективного теплообмена.
- •Вынужденная конвекция (ламинарный и турбулентный режим, критерий рейнольдса).
- •Теплообмен излучением. Основные законы теплообмена излучением.
- •Угловые коэффициенты, их свойства.
- •Свойства угловых коэффициентов.
- •Значение угловых коэф. Для типичных случаев
- •Теплообмен в замкнутой системе (собственное излучение, эффективное, сальдо-поток). Приведенный коэффициент излучения.
- •Защита от излучения с помощью экранов.
- •Степень черноты газа, ее определение.
- •Сложный теплообмен (лучисто-конвективный теплообмен).
- •Классификация топлива, низшая теплота сгорания топлива. Виды горения. Классификация топлива:
- •Коэффициент избытка воздуха при горении топлива. Полное и неполное горение. Расчеты горения топлива.
- •Устройства для сжигания топлива.
- •Физические основы электронагрева.
- •Уравнение неразрывности для сжимаемых и несжимаемых жидкостей.
- •Несжимаемая жидкость
- •Уравнение эйлера для движущейся жидкости. Уравнение эйлера для статики.
- •Уравнение навье-стокса для движения реальной жидкости.
- •Давление, его виды и способы измерения.
- •Струйное движение газов. Свободные струи.Характеристика
- •Струйное движение газов, ограниченные струи.
- •Движение газов в слое кускового и зернистого материала (гранулометрический состав, насыпная плотность и порозность).
- •Движение газов в слое кускового и зернистого материала. Состояние слоя.
- •Принцип расчета дымовой трубы.
- •Классификация огнеупоров.
- •Физические свойства огнеупоров.
- •Пористость и объемная масса
- •Эксплуатационные (рабочие) свойства огнеупоров.
- •Сопротивление печной атмосфере
- •Теплоизоляционные материалы, применяемые в печестроении.
- •Классификация печей. Тепловая работа печей
- •Показатели тепловой работы печей.
- •Вагранки, принцип действия, основные зоны вагранки.
- •Вагранки классифицируют
- •Теплотехнические особенности
- •Влияние различных факторов на зоны горения в вагранке.
- •Использование подогрева дутья в вагранках.
- •Вагранки с обогащением дутья кислородом и охлаждаемым плавильным поясом.
- •Вагранки с водоохлаждаемым плавильным поясом
- •Кислородно-конвертерный процесс, особенности материального и теплового баланса.
- •Классификация дуговых печей, принцип работы, последовательность технологии плавки в дуговых печах.
- •Печи классифицируются:
- •Последовательность технологии плавки в дуговых печах.
- •Состав шлака
- •Основные статьи теплового баланса дуговой печи.
- •Расход тепла
- •Индукционные тигельные печи. Принцип действия и конструкция печи.
- •Нагревательные колодцы, принцип действия и конструкции колодцев.
- •Методические печи для нагрева слитков и заготовок толкательного типа, принцип действия и конструкции, схемы отопления.
- •Нагревательные печи с шагающими балками и шагающим подом, кольцевые печи, принцип действия, схемы отопления.
- •Устройства для использования теплоты отходящих газов, классификация рекуператоров по движению газов.
- •Конструкция и принцип действия игольчатых рекуператоров.
- •Конструкция и принцип действия рекуператоров из стальных труб и радиационных рекуператоров.
- •Принцип действия регенератора.
- •Принцип действия барабанных сушил и сушил в пневмопотоке и кипящем слое.
- •Установки для сушки стержней и литейных форм.
- •Сушила непрерывного действия
- •Сушила с радиационным циклом
Давление, его виды и способы измерения.
В теплотехнике используют понятие избыточного давления (атмосферное).
Различают три вида давления:
Геометрическое;
Статическое;
Динамическое;
Геометрическое давление обусловлено стремлением горячих газов подняться вверх. Из практики это совершенно очевидно.
Если
в результате разности плотности
окружающего газа и воздуха газ перемещается
на высоту h,
то геометрическое давление определяется
по формуле: hг=gH( )
(1)
)
(1)
Статическое давление -- это разность давлений газа, заключенного в сосуде, и окружающей среды.
Статическое давление может быть как положительным, так и отрицательным.
Величина давления может быть определена из опыта, с помощью У-образного манометра:
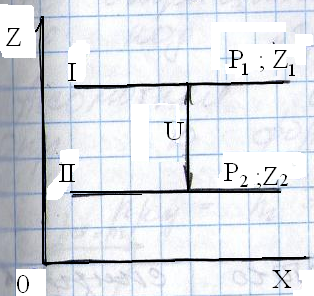
Для определения статического давления манометр устанавливают так, чтобы один конец сообщался с окружающей средой, а другой располагался бы перпендикулярно направлению потока газа (рис 1).
Динамическое давление обусловлено движением газа, опр. по формуле:
h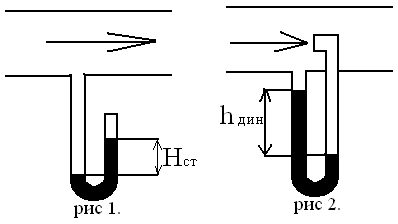 дин=
дин=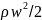
Динамическое давление можно определить опытным путем, для чего один конец манометра подсоединяют перпендикулярно, а другой навстречу направления пока. В рез-те определяется суммарное давление:
h∑=hст+hдин
И измерив заранее статическое давление определяем динамическое давление.
Изменение давления по высоте в неподвижной, несжимаемой жидкости
Для
определения распределения давления
используются уравнение Эйлера для
статики: -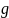 =
=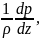 или
или
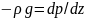 (2)
(2)
Обычно ур-ие решается для 2-х плоскостей (сечений).
 При
условии
получается основное ур-ие статики
жидкости и газов:
При
условии
получается основное ур-ие статики
жидкости и газов:
P2=P1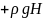 (3)
(3)
P1=P2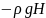 (4)
(4)
Уравнения показывают, что давление линейно падает с высотой, и тем больше, чем выше плотность газа. Для жидкостей говорят, что давление увеличивается по глубине.
Рассмотрим распределение давления газа, находящегося в сосуде. Статическое давление: hст= Pг – Pв (4)
Если Рг<Рв сосуд находится под разряжением.
hраз= - hст=Pв-Pг (5)
Поверхность в каждой точке которой статическое давление равно нулю называется уровнем нулевого избыточного давления.
Для металлургической теплотехники важное значение имеет распределение давления в сосуде с горячим газом.
Р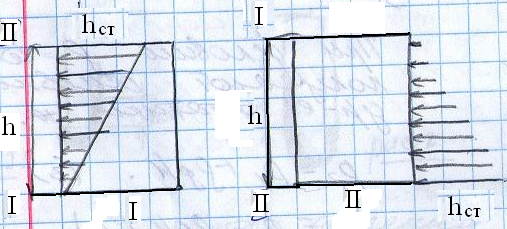 ассмотрим
2 случая распределения давления для
сосуда открытого снизу, и для сосуда
открытого сверху.
ассмотрим
2 случая распределения давления для
сосуда открытого снизу, и для сосуда
открытого сверху.
В случае сосуда открытого снизу в сечении 1 сосуд сообщается с окружающей средой, а давление газа равно давлению окружающего воздуха, т.е. hст(1)=Рг(1) – Рв(1) =0 ,
В сечении 2 давление газа Р22= Р11- 2gh, давление воздуха Рв(2)= Рв(1)- вgh, статическое давление в сечении 2:
hст(2)=Рг(2) – Рв(2) =gh( ) (6)
С другой стороны избыточное давление обусловленное разностью плотностей является геометрическим давлением, поэтому:
hст= h2=gh( ) (7)
Для сосуда открытого сверху статическое давление в сечении 1 равно 0:
hст(1)= Рг(1) – Рв(1) =0
Статическое давление в сечении 2:
hст(2)= Рг(2) – Рв(2) = gh - ( ) (8)
или
- hст(2)= hраз(2) = gh( ) (9)
Из
уравнения (9) следует, что при
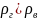 избыточное
давление в сосуде отрицательное, и он
находится под разряжением.
избыточное
давление в сосуде отрицательное, и он
находится под разряжением.
Абсолютная величина разряжения определяется по формуле:
h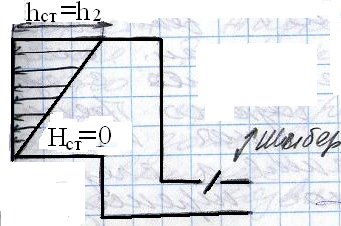 раз=
h2=
gh(
)
раз=
h2=
gh(
)
Если нулевое давление (статическое) находится на уровне входа печи, то над ходом давление в печи выше атмосферного.
Это приводит к выветриванию продуктов сгорания, через отверстия и неплотностях в стенках печи, что вызывает в свою очередь перерасход топлива.
Если нулевое давление поддерживать выше уровня входа печи, то ниже этой плоскости печь будет находится под разряжением, что вызовет подсос холодного окружающего воздуха в печь, это увеличивает расход топлива и повышает окисление металла.
Во втором случае подсос воздуха вызывает больший перерасход топлива, поэтому нулевое давление поддерживают на уровне входа, либо ниже. А для уменьшения выветривания газа печь выполняют более герметично.
УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ ДВИЖЕНИЯ ИДЕАЛЬНОЙ И РЕАЛЬНОЙ ЖИДКОСТИ.
Аналитическое решение уравнения Эйлера, т.е. основного уравнения движения идеальной жидкости наз. уравнением Бернулли, такое уравнение получено как для идеальной, так и для реальной жидкости.

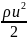 – динамическое
давление
– динамическое
давление
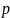 – статическое
давление
– статическое
давление
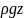 -
геометрическое давление
-
геометрическое давление
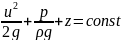
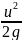 – динамический
напор
– динамический
напор
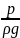 -
статический напор
-
статический напор
- геометрический напор
Уравнение Бернулли для реальных жидкостей учитывает следующее:
распределение скорости в поперечном сечении потока явл. неоднородным, поскольку скорость на стенках равна 0, соответствует неоднородным явл. распределение статического и динамического давления.
часть механической энергии теряется, т.е. переходит в теплоты и рассеивается в следствии трения.

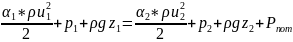
– коэфф. Кориолиса


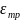 – коэфф.
сопротивления трению
– коэфф.
сопротивления трению
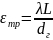
- гидравлический коэфф. трения
 -
длина трубы
-
длина трубы
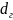 -
гидравлический диаметр
-
гидравлический диаметр
При
ламинарном режиме:
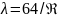
При турбулентном режиме:
если абсолютная шероховатость стенки меньше толщины ламинарного прослоя, то движение рассматривается, как в гидравлически гладкой трубе:
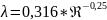
если абсолютная шероховатость стенки больше толщины ламинарного прослоя, то движение рассматривается, как в гидравлически шероховатой трубе:
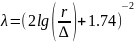
Для приближённых расчётов λ принимают постоянным и равным для кирпичной каналов 0,05, для металлических гладких 0,025, для металлических шероховатых – 0,04.
