
- •Глава 1
- •10.Квадратичная форма и полярная билинейная форма.
- •20. Матрица квадратичных форм.
- •30. Ограничение билинейной (квадратичной формы) на подпространстве
- •10.Определние ортогональности относительно билинейной формы и свойства.
- •20.Ортогональное дополнение и его свойства
- •Глава 2
- •Глава 3
- •1° Теорема об изоморфности евклидовых (унитарных) пространств
- •2° Линейные формы в евклидовых(унитарных) пространствах и скалярные произведения
- •10 Определение и первый критерий
- •20 Ортогональные операторы и ортонормированные базисы
- •30 Ортогональный оператор и сопреж. К немк (Кр-3)
- •40 Матрица ортог. Оператора
- •Глава 4
- •1° Определения и примеры
- •2° Леммы о высшем члене симметрического многочлена
- •3° Основная теорема о симметрических многочленах
1° Определения и примеры
Определение.
R-область целостности,
многочлен fϵR[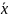 ]
называют симметрическим если он не
меняется при любых перестановках его
переменных. Поскольку всякая перестановка
является произведением транспозиций(перестановок
2х элементов), то многочлен симметрический
если он не меняется при перестановке
любых 2х элементов.
]
называют симметрическим если он не
меняется при любых перестановках его
переменных. Поскольку всякая перестановка
является произведением транспозиций(перестановок
2х элементов), то многочлен симметрический
если он не меняется при перестановке
любых 2х элементов.
Примеры:
f=
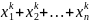
Элементарные симметрические многочлены
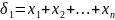
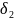 =
=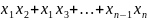
…….
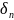 =
=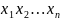
Легко видеть
что сумма, разность, произведение так
же являются симметрическим многочленом.
Поэтому множество всех симметрических
многочленов из R[
]
образует подкольцо в данном кольце
FϵR[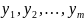 ]
из того же кольца,
]
из того же кольца,
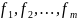 –
симметрические многочлены, F(
)
– симметрический многочлен.
–
симметрические многочлены, F(
)
– симметрический многочлен.
2° Леммы о высшем члене симметрического многочлена
Лемма 1.
Пусть A= - высший член
некоторого симметрического многочлена
f, тогда
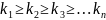 (•)
(•)
Предположим
что (•) не выполняется, т.е
 ,
I 1й номер для которого не
выполняется условие. Поскольку
симметрический, то помимо А он должен
содержать такой одночлен В который
получается из А перестановкой
↔
,
I 1й номер для которого не
выполняется условие. Поскольку
симметрический, то помимо А он должен
содержать такой одночлен В который
получается из А перестановкой
↔
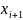 B=
B=
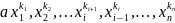 =>
B>A ?!
=>
B>A ?!
Лемма 2.
A=
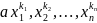 для
которого выполняется (•) найдутся целые
неотрицательные числа
для
которого выполняется (•) найдутся целые
неотрицательные числа
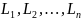 такие
что А является высшим членом
такие
что А является высшим членом
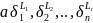 (1),
эти числа
(1),
эти числа
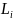 определены
однозначно
определены
однозначно
высший
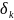 =
=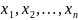 ,
поэтому высший(+) будет
,
поэтому высший(+) будет
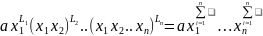 приравниваем
показатели A и получаем
следующую систему
приравниваем
показатели A и получаем
следующую систему
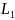 +
+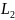 +..
+..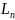 =
=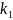 =
=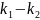
+..
=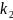 =
-
=
-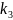
… …
=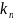 =
=
3° Основная теорема о симметрических многочленах
Теорема.
Пусть fϵR[
]
– симметрический многочлен, R
– область целостности, тогда Ǝ F(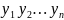 )
ϵ R[
)
ϵ R[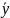 ]
ǀ f=F(
]
ǀ f=F( ),
F определен однозначно,
т.к всякий симметрический многочлен
единственным образом представлен в
виде многочлена от элементарных
симметр-их многочленов
),
F определен однозначно,
т.к всякий симметрический многочлен
единственным образом представлен в
виде многочлена от элементарных
симметр-их многочленов
Если f=0 ,то F=0.
f≠0.Пусть
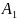 высший член у f. A=
-
выполняется условие (•),тогда по лемме
2
является
высшим у некоторого многочлена F=
.
высший член у f. A=
-
выполняется условие (•),тогда по лемме
2
является
высшим у некоторого многочлена F=
.
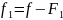 Eсли она равна 0,то искомый
многочлен F=
Eсли она равна 0,то искомый
многочлен F=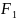 ,
если f≠0 ,то пусть
,
если f≠0 ,то пусть
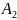 высш член у
,
замети что
выше
чем
т.к. у разности f-
сокращ-ся одинаковый высшие члены =>
остальные члены ниже
высш член у
,
замети что
выше
чем
т.к. у разности f-
сокращ-ся одинаковый высшие члены =>
остальные члены ниже
Пусть
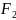 -
произведение степеней элементарных
симметрических многочленов у которых
высш членом является
-
произведение степеней элементарных
симметрических многочленов у которых
высш членом является
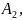 по лемме 2 Ǝ! Такое произведение .
Рассмотрим
по лемме 2 Ǝ! Такое произведение .
Рассмотрим
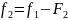 .
Если
.
Если
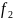 ≡0,
тогдаF=
+
.
Если
≠0,то
такой процесс можно продолжать дальше,
при этом получая цепочку степеней
элементарных многочленов
,
,..
≡0,
тогдаF=
+
.
Если
≠0,то
такой процесс можно продолжать дальше,
при этом получая цепочку степеней
элементарных многочленов
,
,..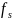 для
высш членом которых выполняется условие
>
>..,
по этой причине этот процесс заканчивается
на шаге
для
высш членом которых выполняется условие
>
>..,
по этой причине этот процесс заканчивается
на шаге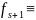 0
и искомый F=
0
и искомый F=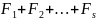 .
В силу того что на каждом шаге
.
В силу того что на каждом шаге
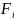 определено однозначно, многочлен F
определен однозначно
определено однозначно, многочлен F
определен однозначно
Следствие
Подкольцо S – симметрических многочленов в R[ ] R-область целостности) изоморфно кольцу всех многочленов R[ ]. Изоморфизм колец называется биекцией м-ду ними с сохранением операций сложения и произведения ‘+’ и‘*’
Рассмотрим Ψ: R[ ]—>S легко видеть при так заданном отображении операции ‘+’ и‘*’ сохраняются. В силу этого всякий элементарный симметрический многочлен представл-я в виде многочлена от элементарных симметрических, отображение Ψ – сюрьективно. В силу того, что такое представление единственно =>отображение является инъективным
