Глава 4

Гл 4 Пр1 Кольцо многочлена от нескольких переменных

основные понятия

R- коммутативное ассоциативное унитарное кольцо

- независимые переменные

Определение. Одночленом относительно данных переменных называется выражение вида 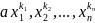,где , , 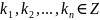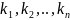- называются степенями одночлена относительно переменных, k= - полная степень одночлена.

Два одночлена с одинаковыми степенями по всем переменным называются подобными. Их можно складывать + =

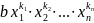Произвольные одночлены можно перемножать

=

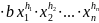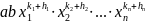
Определение. Многочленом от переменных называется конечная сумма одночленов от этих переменных

f( )= (*)

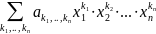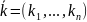
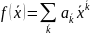
Определение. Многочлен, все коэффициенты которого =0 называется нулевым многочленом.

Два многочлена называются равными если их разность – нулевой многочлен.

Максимальная из степеней одночленов, составляющих данный многочлен, называется степенью многочлена [ ].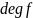

Можно рассматривать степени и относительно отдельных одночленов. Максимальная из степеней многочлена относительно обозначается .

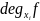Кольцо многочленов относительно нескольких переменных

Операции для одночленов естественным образом переносятся и на многочлены.

Множество всех многочленов от n-переменных с коэффициентами из 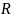обозначается

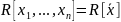
Предложение

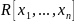с операциями является коммутативным ассоциативным унитарным кольцом.

доказательство очевидно

Возможна ситуация

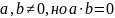
Например, рассмотрим кольцо

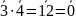
Ненулевые элементы a и b кольца, такие что называются делителями нуля.

Определение. Коммутативное ассоциативное унитарное кольцо без делителей нуля называется областью целостности

Пример ,всякое поле

Теорема. Если R-область целостности, то и - область целостности.

Индукция по n

База: n=1

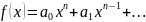
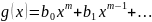, где 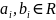-область целостности

(Поскольку R-область целостности n,значит )

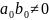Индукционный переход: предположим, что утверждение верно для колец переменных с количеством переменных <n.

Всякий многочлен от n-переменных можно рассматривать ,как многочлен от одной конкретной переменной

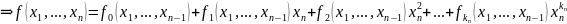
При этом коэффициентами являются многочлены из . Таким образом

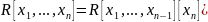
Согласно индукционному предположению 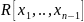- область целостности. Согласно (**) можно повторить и получим ,что -область целостности.

Следствие. Если R-область целостности, то в кольце 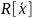степень

Определение. Многочлен, все одночлены которого имеют одинаковую степень r , называются однородным многочленом степени r или формой степени r.

Пример: Форма степени 2квадратичная форма

Представим многочлены и 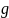в виде суммы однородных многочленов

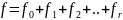
Тогда произведение все старшие (наибольшие)степени 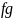будут содержаться в

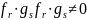, т.к. в этом кольце нет делителей нуля

Значения многочлена от нескольких переменных

Пусть кольцо , причём

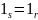
Заметим

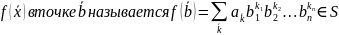
Предложение

(+)

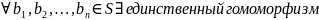
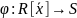
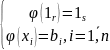
Гомоморфизм колец- это отображение, при котором сохраняются операции.

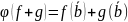
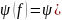
Теорема о тождестве

Известно, что два различных многочлена от одной переменной над R могут иметь одинаковое значение только на конечном количестве точек n: если 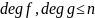, то их значения совпадают не более, чем в n точках.

Если R-бесконечное

.

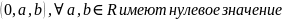Теорема.R- бесконечная область целостности

Если 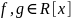принимают одинаковое значение во всех 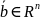, то многочлен

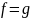
Поэтому . Достаточно доказать, что если принимает значение 0 во всех точках ,то - нулевой многочлен.

Предположим противное

Докажем, что точка, в которой принимает ненулевое значение.

Индукция по n-количеству переменных

, то

Иначе бы это означало, что многочлен от одной переменной имеет бесконечно много корней.

Индукционный переход

Предположим, что утверждение верно для многочленов с числом переменных <n.

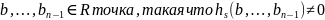
, причём - 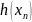ненулевой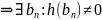

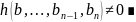
Следствие(о несущественности алгебраических неравенств).Пусть R-бесконечная область целостности 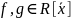Если принимают одинаковые значения во всех точках , в которых 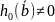, ,…, , где . Тогда

Рассмотрим многочлен 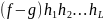легко видеть, что он принимает нулевое значение во всех точках без исключения.Поскольку , то

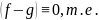
Лексикографический порядок на множестве одночленов

Введём на множестве одночленов порядок

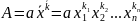
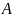выше ( )

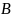Если номер i, такой что до i степени это отношение линейного порядка со свойствами:

Предложение. В кольце многочленов , -область целостности

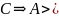
, (транзитивность)

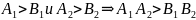
Рассмотрим

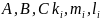
Пусть - минимальный из индексов при котором не все из показателей одинаковы 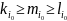причём хотя бы одно из этих неравенств строгое

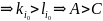
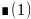
При умножении 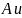на , к показателям переменных в прибавляются одни те же слагаемые

.

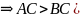
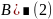
Высшие члены многочленов

Определение. Высшим членом многочлена называется одночлен, который выше всех других одночленов этого многочлена.

Записав сначала самый высший, затем высший из оставшихся и т.д., получим запись многочлена в лексикографическом порядке.

Замечание. Не следует путать высший член и старший. Старший член имеет высшую целую степень.

Предложение. В кольце , R-область целостности. Высший член произведения многочленов равен произведению высших членов этих многочленов.

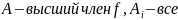
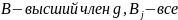
У 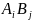-все многочлены

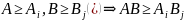
Причём, если только в 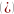не оба равенства, то .

Это означает, что после приведения подобных в произведении 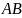ни с чем не сократится, поэтому -высший член

Гл 4 Пр 2 Симетрические многочлены